扩散II_牛客网

牛客网编程题 扩散II

牛客网原链接

题目描述

作为牛客王国的探险先锋，牛牛来到了一片新的大陆。这是一个工业化程度很高的大陆，遍地都是工厂，有些工厂之间有管道相连。这片大陆一共有 \(n\) 个工厂，有 \(n\) 对工厂之间有管道相连，因为工厂之间需要合作，所以这 \(n-1\) 个管道保证任意两个工厂都可以通过管道互相抵达。每根管道的长度都是1.（换言之，\(n\) 个工厂与 \(n-1\) 根管道组成了无根树）。

牛牛发现，从这片大陆开始工业化以来，一共发生了 \(m\) 次污染。
每次污染用3个参数 \(x_i, y_i, z_i\)表示在第 \(x_i\) 个工厂发生了污染，
影响了所有和第 \(x_i\)个工厂的最短距离小于等于 \(y_i\) 的工厂，这些被影响的工厂（包括 \(x_i\)）的污染指数都增加了 \(z_i\)。

一开始所有的工厂污染指数为0.
现在牛牛想知道，在发生了这m次污染之后，每个工厂的污染指数是多少。

示例1

输入

5,5,[1,2,3,3],[2,3,4,5],[1,2,3,4,5],[1,1,1,1,1],[1,2,3,4,5]

输出

[3,6,14,7,8]

说明

在1，2，3，4，5分别发生了距离为1的污染，他们的影响为分别为1，2，3，4，5
1发生的污染影响了1，2
2发生的污染影响了1，2，3
3发生的污染影响了2，3，4，5
4发生的污染影响了3，4
5发生的污染影响了3，5
最终五个工厂污染指数为[3,6,14,7,8]

备注

\(1<=n,m<=2e5, 1<=u,v,x_i<=n, 1<=y_i<=50, 1<=z_i<=1e4\)

第一个参数n代表工厂数量
第二个参数m代表污染发生次数
第三、四个参数vector u,v各自包含n-1个元素
第五、六、七个参数vector x,y,z各自包含m个元素，代表m次污染

解题思路

最简单的解法就是对每个 \(x_i\) 使用 bfs 增加污染值，但是这种方法的时间复杂度最差为 \(O(n^2)\)，不能AC。
另一种方法：考虑以每个 \(x_i\) 扩散出来的路径，在使用 \(O(n)\) 空间情况下，我们能否用上次扩散的路径递推得到下次路径？并且在多个 \(x_i\) 同时存在的情况下如何递推？（注意我们并不能使用辅助数组来记录访问过的节点。这会很消耗资源，并且并不高效。）答案是可以，只使用 \(O(n)\) 空间来对所有污染值路径进行递推，每一步递推意味着距离减少1，所以时间复杂度为 \(O(n*max(y))\)。

下面举个例子来说明这个过程：
假设这样一个工厂连接图，输入的指令是 \(x=3, y=3, z=7\)。

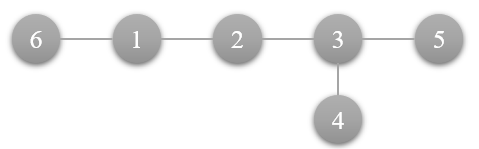
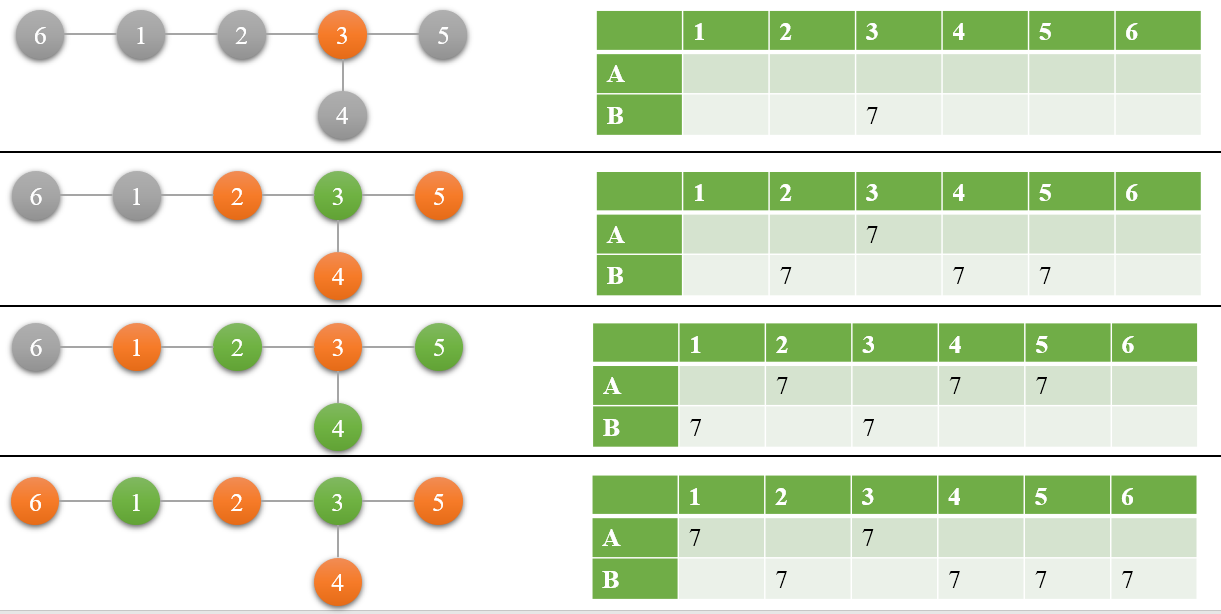
用两个数组（A，B）来保存路径距离源点 \(3\) 的距离为奇数和偶数的点上的污染值，这样最终的结果就是两个数组相加即可。这两个数组并不固定哪个是奇数哪个是偶数，只是固定B一点包含传播最远的点。

1. 开始的时候，源点为 3, 所以 B[3] = 7;
2. 传播一步得到新增加的点，B[2,4,5] = 7, A 就是原先的 B。
3. 。。。
   
   更新公式：

     C = A
     for i in range(1,n):
          for neig in grpha[i]:
                 C[i] += B[neig] - A[i] # 如果 i 已经访问过，那么 C[i] = A[i], 如果未访问过 C[i] = B[i]
     A = B
     B = C

不同的源点\(x\)之间可以共用一个数组，并不影响最终结果，不同的距离 \(y\) 意味这跌打更新的轮次不同，最长的 \(y\) 可能最先开始，每次迭代减少一个距离。所以按 \(y\) 的倒序处理每个源点。
综上代码如下：
!!! 测试数据里面有坑，好像有 \(x_i=0\)

#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution {
public:
    struct Pul{
        int x,y,z;
    };
    vector<int> solve(int n, int m, vector<int>& u, vector<int>& v,
                      vector<int>& x, vector<int>& y, vector<int>& z) {
        vector<vector<int>> g(n+1, vector<int>()); // graphe 图
        for(int i=0; i<u.size(); i++){
            g[u[i]].push_back(v[i]);
            g[v[i]].push_back(u[i]);
        }
        vector<Pul> ps;
        for(int i=0; i<x.size(); ++i){
            ps.push_back({x[i], y[i], z[i]});
        }
        sort(ps.begin(), ps.end(), [](Pul& a, Pul& b)->bool{ return a.y<b.y; } );
        vector<int> a(n+1, 0), b(n+1, 0);
        for(int sz=ps.back().y; sz>=0; --sz){ // 倒序处理
            vector<int> c(a);
            for(int i=0; i<=n; i++){
                for(auto& neig:g[i]) c[i] += b[neig] - a[i];
            }
            while(ps.size()){
                auto& tmp = ps.back();
                if(tmp.y < sz) break;
                c[tmp.x] += tmp.z;
                ps.pop_back();
            }
            swap(a,b);
            swap(b,c);
        }
        for(int i=0; i<=n; i++) a[i] += b[i];
        a.erase(a.begin());
        return a;
    }
};