线段树（原理简述+C++代码）

线段树简述

线段树的特点：

• 操作逻辑是树的逻辑（左右子节点概念）
• 底层数据存储却是用数字实现的。说白了，线段树对应的是一棵完全二叉树，每个节点在数组中的位置就是该该节点在层序遍历中的序号（从1开始）。

基于数组实现我们能方便的访问一个节点的左右子节点，设当前节点存储序号 idx ，则左右子节点为存储序号分别为 idx*2 和 idx*2+1。

线段树有什么用?

考虑一个场景，我们有一个数组 ori[1:n]，在任意时刻我们希望把某区间 ori[a:b] 内的数据同时更新（加上某个数），或者是查询区间 ori[a:b] 内所有数字的和。要实现这样一个功能，如果采用原始的实现的话，操作复杂度是 \(O(b-a)\)，在区间较大时复杂度不可接受。

1. 优化查询复杂度，如果我们能把 \(b-a\) 拆分成为 2 的幂次的加和，并且存储了这些区间的信息，那么我们可以将这些区间的的加起来即为总和。优化后复杂度为 \(O(log_2(n))\)。
2. 优化更新复杂度，引入一个 lazy 优化（需要额外的\(O(n)\) 空间），同样能把更新复杂度优化到 \(O(log_2(n))\)。lazy 用

而实现这两点刚好就可以用线段树来实现，线段树的每个节点包含的信息是某区间内的信息。如下图

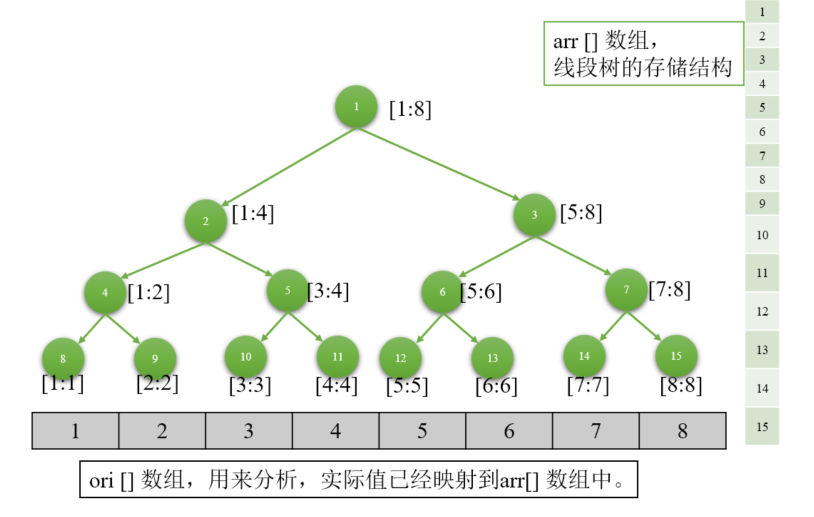
在整个线段树的实现中，我们只有一个数组arr[]用来保存节点的值（某区间内数的和）。原始数组 ori[] 已经被映射到了 arr[] 中，不再单独占用存储空间。

• 考虑查询sum(ori[3:7]) ，拆分可得 sum(ori[3:7]) = sum(ori[3:4]) + sum(ori[5:6]) + sum(ori[7,7])，即访问 arr[] 的 5,6,14 号节点即可。显然借助 arr[] 就可以实现 \(log(N)\) 复杂度；
• 更新时我们同样可以将区间拆分，同样考虑更新区间 ori[3:7]， 拆分为 ori[3:4], ori[5:6], ori[7:7]， ori[3:4] 对应 arr[] 的 5 号节点，更新到 5 号节点后不在往下更新，映入一个 lazy 变量来缓存更新信息，待下次查询或者更新到 5 节点的子节点时再把该缓存信息更新到 子节点。所以也能实现 \(log(N)\) 复杂度。lazy 用和 arr 同样大小的数组存储。

C++ 代码

在初始化 arr[] 和 lazy[] 时长度为 4 倍 ori[] 长度。

• 代码难点，lazy 的正确更新。

// 线段树(加和)
template<class T>
class LineVec {
public:
	LineVec<T>(int _sz):sz(_sz), arr(_sz *4, 0), lazy(_sz *4, 0){}

	// 区间 [l,r] 更新 (同时+val)
	void update(int l, int r, T val) {
		_update(1, 1, sz, l, r, val);
	}
	
	// 区间 [l,r] 求和
	T query(int l, int r) {
		return _query(1, 1, sz, l, r);
	}

private:
	int sz; // [1,sz] 边界
	std::vector<T> arr, lazy; // arr 存储值，lazy 存储待加值，被某区间所有数字共享

	// 对于某节点 arr_index, 其所代表的区间为 [cl,cr] ，总有该区间内和为 arr[arr_index] + lazy[arr_index]*(cr-cl+1)
	// 当我们 update 或者是 query 遇到一个节点时，总是想要把 lazy[arr_index] 传递到子节点，并且把当前该节点的 lazy 置0
	void _elimate_lazy(int arr_idx, int cl, int cr) {
		if (lazy[arr_idx] == 0) return;	 // 已清除
		int l_child = arr_idx << 1, r_child = l_child + 1;
		if (l_child < lazy.size()) lazy[l_child] += lazy[arr_idx]; // 传递到子节点
		if (r_child < lazy.size()) lazy[r_child] += lazy[arr_idx]; // 传递到子节点
		arr[arr_idx] += lazy[arr_idx] * (cr - cl + 1);	// 将当前区间和放到 arr[arr_index] 中
		lazy[arr_idx] = 0;	// 清除 lazy[arr_index]
	}

	void _update(int arr_idx, int cl, int cr, int l, int r, T& val) {
		if (l <= cl and cr <= r) {
			lazy[arr_idx] += val;
			_elimate_lazy(arr_idx, cl, cr);
		}
		else {
			_elimate_lazy(arr_idx, cl, cr);

			// 和区间不被一个节点所包含， [l,r] 和 [cl,cr] 公共部分的和合并到 arr[arr_index] 中
			arr[arr_idx] += val * std::max(0, std::min(r, cr) - std::max(l, cl) + 1);
			
			int mid = (cl + cr) >> 1;
			if (mid >= l) {
				_update(arr_idx << 1, cl, mid, l, r, val); // 左孩子掌管的区间
			}
			if (mid < r) {
				_update(arr_idx << 1 | 1, mid + 1, cr, l, r, val); // 右孩子掌管的区间
			}
		}
	}

	T _query(int arr_idx, int cl, int cr, int l, int r) {
		// 总是应该把 lazy 传递
		_elimate_lazy(arr_idx, cl, cr);

		T ret = 0;
		if (l <= cl and cr <= r) {
			ret = arr[arr_idx];
		}
		else {
			int mid = (cl + cr) >> 1;
			if (mid >= l) {
				ret += _query(arr_idx << 1, cl, mid, l, r);
			}
			if (mid < r) {
				ret += _query(arr_idx << 1 | 1, mid + 1, cr, l, r);
			}
		}
		return ret;
	}
};