刷题&补题日记 | 6-12小白月赛
三人战队第一次磨合,成功发现了大家都是好菜好菜啊
部分题解(写多了就不想看了):
T1:dd爱科学
【问题链接】
https://ac.nowcoder.com/acm/contest/17681/A
【问题大意】
一个长度为N仅包含大写字母的字符串,修改若干字母使其呈按位非递减形态,问至少需要修改几个字母?
【思路】
求出最长不降子序列用N减一下就好了。
*如何求最长不降子序列(LIS)
首先以添加第一个数作为第一个合法升序子序列,接下来依次添加后面的元素。若添加的元素比当前序列最后一个元素大,则将其添加到该子序列尾部。否则在该序列中从左到右找到第一个比其大的最小元素,将其替换掉。使用二分查找,时间复杂度为O(nlogn)
例:数组 [1,7,8,2,3,4,10,11] ,开始时序列为[1]。后面的元素1比7大,添加至末尾,8比7大,添加至末尾,形成[1,7,8]。下一个元素2小于7,将其替换.[1,2,8]。下一个元素3小于8,将其替换.[1,2,3]。下面的元素依次添加进来,形成[1,2,3,4,10,11],最长子序列长度为6。这是思路的关键,可以手写几个例子体会一下。
*STL二分
1 int pos1=lower_bound(a,a+n,k)-a; //a数组中第一个大于等于k的值 2 int pos2=upper_bound(a,a+n,k)-a; //a数组中第一个大于k的值 3 int pos3=lower_bound(a,a+n,k,greater<int>())-a; //a数组中第一个小于等于k的值 4 int pos4=lower_bound(a,a+n,k,greater<int>())-a; //a数组中第一个小于k的值
【代码】
1 #include <bits/stdc++.h> 2 using namespace std; 3 int a[1000010],d[1000010],n,len=0; 4 int main(){ 5 cin>>n;getchar(); 6 for (int i=1;i<=n;i++) { 7 char c=getchar(); 8 a[i]=c-'A'; 9 } 10 d[0]=-1; 11 for (int i=1;i<=n;i++){ 12 if (a[i]>=d[len]){ 13 len++; 14 d[len]=a[i]; 15 } 16 else { 17 int pos=upper_bound(d+1,d+len,a[i])-d;//找到第一个比a[i]大的字母 18 d[pos]=a[i]; 19 } 20 } 21 cout<<n-len; 22 return 0; 23 }
T2:dd爱探险
【问题链接】
https://ac.nowcoder.com/acm/contest/17681/B
【问题大意】
星际中有n个空间站,任意两个空间站间可以相互跳跃,由空间站x跳跃到空间站y所需要的代价为P[x][y],dd可以任意选择出发的空间站,并通过恰好n−1次跳跃把所有空间站跳完。并且dd必须选择2次跳跃,其中一次跳跃中进行重力加速,另一次跳跃中进行反重力加速,重力加速会导致当前跳跃代价变为0,反重力加速会导致当前跳跃代价翻倍,问跳完所有空间站所需要最小代价。
【思路】
状压DP。在最短Hamilton路径的基础上考虑2次跳跃即可。
*首先来看一道经典的状压DP——最短Hamilton路径
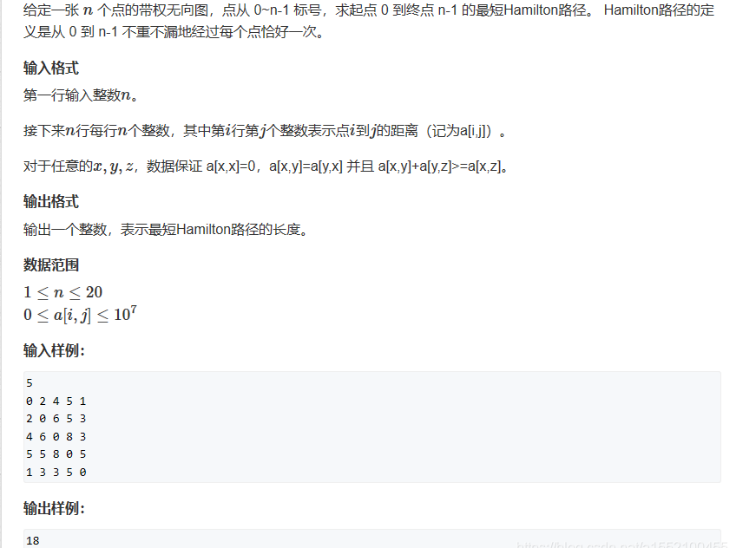
暴力20!必超时,因此考虑动态规划。
状压dp的基本思路是把每一个点的状态用二进制表述出来,再转换为十进制数,在此基础上进行dp。
我们首先构造一个n位的二进制数,其中第i位为1表示第i点已经去过了,第i位为0表示第i点还没去过。然后将这个二进制数转为十进制数x。另外我们还要知道最后一个到达的点y(因为去下一个点要从y出发)。我们使用dp[x][y]进行动归。简而言之,x体现出那几个点去过,y记录去过的最后一个点。
在此基础上构建动态转移方程:
1 dp[i][j]=min{dp[i-(1<<j)][k]+dis[k][j],k∈所有已经去过的点}
有一点懵逼是吧。举个例子,比如说n=5,目前已经去过了1,2,4,5四个节点,(11011)2=(27)10,其中第4个节点是最后一个去的。也就是说我们现在要求的是dp[27][4]
最后一步可能是1->4 , 2->4 , 5->4,三种情况求最小值,即:
1 dp[11011][4]=min{dp[11001][1]+dis[1][4],dp[11001][2]+dis[2][4],dp[11001][1]+dis[5][4]}
为了方便理解这边我把x写成了二进制的形态。在走最后一步之前4号点是没去过的嘛,因此是11001
同理:
1 dp[11011][1]=min{dp[01011][2]+dis[2][1],dp[01011][4]+dis[4][1],dp[01011][5]+dis[5][1]} 2 dp[11011][2]=min{dp[10011][1]+dis[1][2],dp[10011][4]+dis[4][2],dp[10011][5]+dis[5][2]} 3 dp[11011][5]=min{dp[11010][1]+dis[1][5],dp[10011][2]+dis[2][5],dp[10011][5]+dis[4][5]}
【代码】
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int MAXN=1<<16; 4 int dp[MAXN][16],n,dis[20][20],tag[MAXN]; 5 int main(){ 6 memset(dp,0x3f,sizeof(dp)); 7 scanf("%d",&n); 8 for (int i=0;i<n;i++) 9 for (int j=0;j<n;j++) 10 scanf("%d",&dis[i][j]); 11 dp[1][0]=0;//初始化 12 for (int i=1;i<(1<<n);i++){ 13 for (int j=0;j<n;j++){ 14 if ((i>>j)%2==0) continue; //如果第j位是0,说明状态i下j是未经过的点,此时j不可能作为最后一点,舍弃这种情况 15 int x=i-(1<<j);//状态i去掉j号点的状态 16 for (int k=0;k<n;k++){ 17 if ((x>>k)%2==0) continue; //如果第k位是0,说明状态x下k是未经过的点,此时k不可能作为倒数第二点,舍弃这种情况 18 if (dp[x][k]+dis[k][j]<dp[i][j]) dp[i][j]=dp[x][k]+dis[k][j];//动态转移方程 19 } 20 } 21 } 22 printf("%d",dp[(1<<n)-1][n-1]); 23 return 0; 24 }
回到原题。因为要考虑两次跳跃,我们构建一个三层的dp。dp[x][y][0]表示无跳跃层dp[x][y][1]表示跳跃一次层,dp[x][y]表示跳跃两次层。
另外值得一提的是初始化与答案处理也要有所区别,因为这道题的起点终点是不固定的,而模板题起点终点固定。
【代码】
1 #include <bits/stdc++.h> 2 using namespace std; 3 int dis[16][16],dp[1<<16][16][3],n; 4 int main(){ 5 memset(dp,0x3f,sizeof(dp)); 6 cin>>n; 7 for (int i=0;i<n;i++) 8 for (int j=0;j<n;j++) 9 cin>>dis[i][j]; 10 for(int i=0;i<n;i++) dp[1<<i][i][0]=0;//初始化不能简单的dp[1][0][0]=0,因为起点不固定 11 for (int i=1;i<(1<<n);i++){ 12 for (int j=0;j<n;j++){ 13 if ((i>>j)%2==0) continue; 14 int x=i-(1<<j); 15 for (int k=0;k<n;k++){ 16 if ((x>>k)%2==0) continue; 17 dp[i][j][0]=min(dp[i][j][0],dp[x][k][0]+dis[k][j]);//不考虑跳跃 18 dp[i][j][1]=min(dp[i][j][1],min(dp[x][k][0],dp[x][k][1]+dis[k][j]));//这一步可以作为重力跳跃,也可不做重力跳跃 19 dp[i][j][2]=min(dp[i][j][2],min(dp[x][k][2]+dis[k][j],dp[x][k][1]+2*dis[k][j]));//这一步可以作为反重力跳跃,也可不做反重力跳跃 20 } 21 } 22 } 23 int ans=1e9; 24 for (int j=0;j<n;j++) ans=min(ans,dp[(1<<n)-1][j][2]);//取出结果最大值 25 cout<<ans; 26 return 0; 27 }
T3:dd爱旋转
【问题链接】
https://ac.nowcoder.com/acm/contest/11211/E
【问题大意】

【思路】
规律题。两次操作1,两次操作2都能使矩阵复原,因此只需分别考虑操作1和操作2的次数是奇数还是偶数即可。
【代码】
1 #include <bits/stdc++.h> 2 using namespace std; 3 int n,m,x,a[1001][1001]={0},op1=0,op2=0; 4 int t[1001][1001]={0};//有点粗暴 5 void res1(){//操作1 6 for (int i=1;i<=n;i++) 7 for (int j=1;j<=n;j++) 8 t[n-i+1][n-j+1]=a[i][j]; 9 for (int i=1;i<=n;i++) 10 for (int j=1;j<=n;j++) 11 a[i][j]=t[i][j]; 12 } 13 void res2(){//操作2 14 for (int i=1;i<=n;i++) 15 for (int j=1;j<=n;j++) 16 t[n-i+1][j]=a[i][j]; 17 for (int i=1;i<=n;i++) 18 for (int j=1;j<=n;j++) 19 a[i][j]=t[i][j]; 20 } 21 int main(){ 22 scanf("%d",&n); 23 for (int i=1;i<=n;i++) 24 for (int j=1;j<=n;j++) 25 scanf("%d",&a[i][j]); 26 scanf("%d",&m); 27 while (m--){ 28 scanf("%d",&x); 29 if (x%2) op1++; 30 else op2++; 31 } 32 if (op1%2) res1(); 33 if (op2%2) res2(); 34 for (int i=1;i<=n;i++){ 35 for (int j=1;j<=n;j++) printf("%d ",a[i][j]); 36 printf("\n"); 37 } 38 return 0; 39 }
T4:dd爱框框
【问题链接】
https://ac.nowcoder.com/acm/contest/11211/F
【问题大意】
读入n,x,给出n个数a[1],a[2],……,a[n],求最小的区间[l,r],使a[l]+a[l+1]+……+a[r]≥x,若存在相同长度区间,输出l最小的那个。
【思路】
确实是个水题。用两个指针l,r记录当前区间的上界和下界,区间和小于x时右移r,大于x时右移l并迭代最小长度,时间复杂度O(n)。
【代码】
1 #include <bits/stdc++.h> 2 using namespace std; 3 int a[10000001]={0}; 4 int read(){ 5 int x=0,y=1; 6 char c=getchar(); 7 while (c<'0'||c>'9') {if (c=='-') y=-1;c=getchar(); } 8 while (c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar(); } 9 return x*y; 10 } 11 int main(){ 12 int n,x,l=1,r=1,sum=0,mind=1e8,minl,minr; 13 n=read(); x=read(); 14 while (r<=n){ 15 a[r]=read(); 16 sum+=a[r]; 17 while (sum-a[l]>=x) sum-=a[l],l++; 18 if (r-l+1<mind&&sum>=x){ 19 mind=r-l+1; 20 minl=l; 21 minr=r; 22 } 23 r++; 24 } 25 cout<<minl<<' '<<minr; 26 return 0; 27 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号