通过不同的遍历（前序 中序，后序 中序）构造二叉树

1、从前序与中序遍历序列构造二叉树

 

给定一棵树的前序遍历 preorder 与中序遍历  inorder。请构造二叉树并返回其根节点。

 

示例 1:

 

 


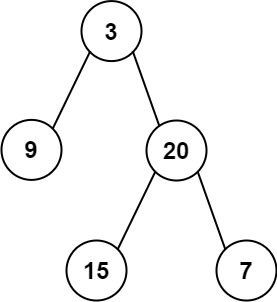
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

递归

思路：对于任意一颗树而言，前序遍历的形式总是

[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

 

人话：

preorder第一个元素为root，在inorder里面找到root，在它之前的为左子树（长l1），之后为右子树（长l2）。preorder[1]到preorder[l1]为左子树,之后为右子树，分别递归。

 

细节

在中序遍历中对根节点进行定位时，一种简单的方法是直接扫描整个中序遍历的结果并找出根节点，但这样做的时间复杂度较高。我们可以考虑使用哈希表来帮助我们快速地定位根节点。对于哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置。在构造二叉树的过程之前，我们可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，我们就只需要O(1) 的时间对根节点进行定位了。

 

实现：python

 1 class Solution:
 2     def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
 3         def myBuildTree(preorder_left: int, preorder_right: int, inorder_left: int, inorder_right: int):
 4             if preorder_left > preorder_right:
 5                 return None
 6             
 7             # 前序遍历中的第一个节点就是根节点
 8             preorder_root = preorder_left
 9             # 在中序遍历中定位根节点
10             inorder_root = index[preorder[preorder_root]]
11             
12             # 先把根节点建立出来
13             root = TreeNode(preorder[preorder_root])
14             # 得到左子树中的节点数目
15             size_left_subtree = inorder_root - inorder_left
16             # 递归地构造左子树，并连接到根节点
17             # 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
18             root.left = myBuildTree(preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1)
19             # 递归地构造右子树，并连接到根节点
20             # 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
21             root.right = myBuildTree(preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right)
22             return root
23         
24         n = len(preorder)
25         # 构造哈希映射，帮助我们快速定位根节点
26         index = {element: i for i, element in enumerate(inorder)}
27         return myBuildTree(0, n - 1, 0, n - 1)

 

 

2、从中序与后序遍历序列构造二叉树

同理：

 1 class TreeNode(object):
 2     def __init__(self, val=0, left=None, right=None):
 3         self.val = val
 4         self.left = left
 5         self.right = right
 6 
 7 
 8 class Solution(object):
 9     def buildTree(self, inorder, postorder):
10         """
11         :type inorder: List[int]
12         :type postorder: List[int]
13         :rtype: TreeNode
14         """
15 
16         def build(post_left, post_right, in_left, in_right):
17             if post_left > post_right:
18                 return None
19 
20             post_root = post_right  # 4
21             in_root = mp_ind[postorder[post_root]]  # 1
22 
23             root = TreeNode(postorder[post_root])
24             right_size = in_right - in_root # 3
25             root.left = build(post_left, post_right-right_size-1, in_left, in_root-1)
26             root.right = build(post_right-right_size, post_right-1, in_root+1, in_right)
27 
28             return root
29 
30         n = len(inorder)
31         mp_ind = {val: i for i, val in enumerate(inorder)}
32 
33         return build(0, n - 1, 0, n - 1)

 

posted @ 2021-12-29 15:05  r1-12king  阅读(117)  评论(0)    收藏  举报