【题解】(DP专题) P1736 创意吃鱼法
在阅读本篇题解前,可以先去看下题目描述:
传送🚪1号:P1736 创意吃鱼法 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这道题目,其实是另一道DP练习题の加强版
如果觉得自己是个巨蒟蒻,可以先看一下削弱版:
传送🚪2号:P1387 最大正方形 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
∵有大佬已经讲过这道题了
又∵大佬讲得比我好很多
∴直接上链接(自己去领会,时间为1:08:58~1:20:28)B4.动态规划入门_哔哩哔哩_bilibili
看完记得嘲讽自己一句

P1387の思路理清之后,这题の思路也就好理解得多了
P1387の状转和本题の状转并没有本质上の区别
P1387の状转是这样の:

F(i,j)=min{F(i-1,j),min{F(i,j-1),F(i-1,j-1)}}+1 (g(i,j)!=0)
F(i,j)=0 (g(i,j)=0)
而这题只需要加亿点数组记录状态即可(也就6个二维数组而已,QAQ)
为了好理解些,先附上代码(前方高能,蒟蒻请迅速跳过)
#include<bits/stdc++.h> using namespace std; int n,m,d1[2502][2502],d2[2502][2502],d3[2502][2502],d4[2502][2502]; int v1[2502][2502],v2[2502][2502],ans; bool g[2501][2501]; int main() { cin>>n>>m; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>g[i][j]; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(g[i][j]) d1[i][j]=0;else d1[i][j]=min(d1[i-1][j-1],d1[i][j-1])+1; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(g[i][j]) d2[i][j]=0;else d2[i][j]=min(d2[i-1][j-1],d2[i-1][j])+1; for(int i=1;i<=n;i++) for(int j=m;j>=1;j--) if(g[i][j]) d3[i][j]=0;else d3[i][j]=min(d3[i-1][j+1],d3[i][j+1])+1; for(int i=1;i<=n;i++) for(int j=m;j>=1;j--) if(g[i][j]) d4[i][j]=0;else d4[i][j]=min(d4[i-1][j+1],d4[i-1][j])+1;for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(g[i][j]){v1[i][j]=min(v1[i-1][j-1],min(d1[i][j-1],d2[i-1][j]))+1;ans=max(ans,v1[i][j]);} for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(g[i][j]){v2[i][j]=min(v2[i-1][j+1],min(d3[i][j+1],d4[i-1][j]))+1;ans=max(ans,v2[i][j]);} cout<<ans<<'\n'; return 0; }
好吧,除了有亿点长,还是挺工整的(强迫症の福音)
说下我的思路:
首先,根据题目描述可知,我们的目标是找到某条对角线上全部是1,其余部分都是0的01正方形
例如:
1 0 0
0 1 0
0 0 1
当然,也可以是这样:
0 0 1
0 1 0
1 0 0
作为一个十分大(ju)佬(ruo)的人,这点自然很容易想到(PS.此处“大佬”为词类活用,名词作形容词)
然后,就可以把它分成三个部分(如下图)
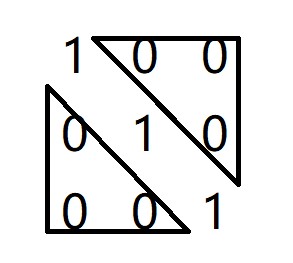
三个部分划分好以后,就可以用下面の代码进行处理了:
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(g[i][j]) d1[i][j]=0;else d1[i][j]=min(d1[i-1][j-1],d1[i][j-1])+1; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(g[i][j]) d2[i][j]=0;else d2[i][j]=min(d2[i-1][j-1],d2[i-1][j])+1; for(int i=1;i<=n;i++) for(int j=m;j>=1;j--) if(g[i][j]) d3[i][j]=0;else d3[i][j]=min(d3[i-1][j+1],d3[i][j+1])+1; for(int i=1;i<=n;i++) for(int j=m;j>=1;j--) if(g[i][j]) d4[i][j]=0;else d4[i][j]=min(d4[i-1][j+1],d4[i-1][j])+1;
因为有下面の4种情况,所以要用四个二维数组来记录
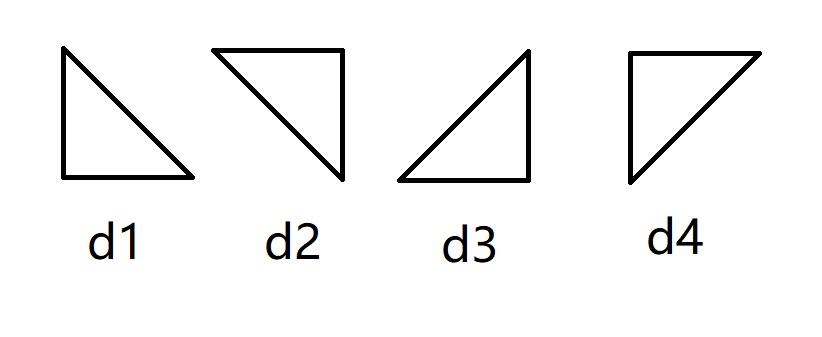
这样,就可以用与P1387类似の状转方程进行状转了:
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(g[i][j]){v1[i][j]=min(v1[i-1][j-1],min(d1[i][j-1],d2[i-1][j]))+1;ans=max(ans,v1[i][j]);}
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(g[i][j]){v2[i][j]=min(v2[i-1][j+1],min(d3[i][j+1],d4[i-1][j]))+1;ans=max(ans,v2[i][j]);}
写好了,那就提交吧
However,事情并没有那么简单。。。
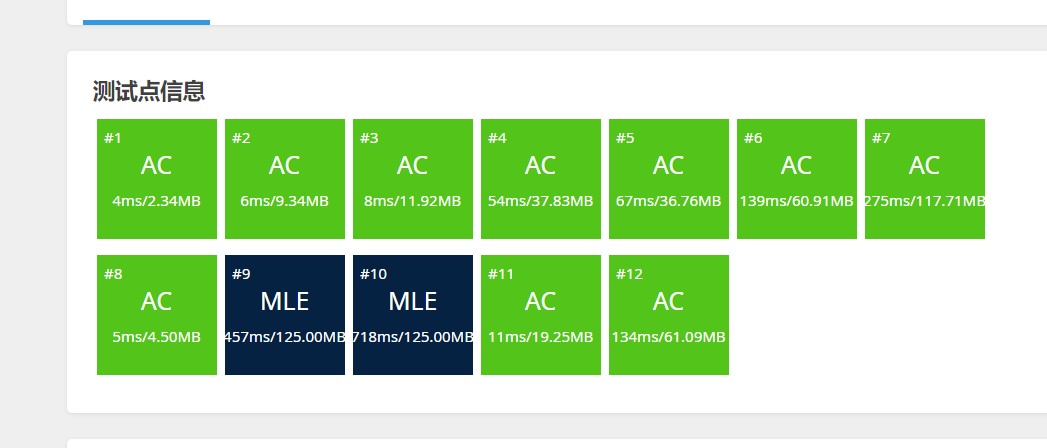
两个MLE,让我知道了事态の严峻
Then,在一旁吃瓜のTheSky233大佬提醒了我:
你不觉得,4个字节のint有点逊么?2个字节のshort不香吗?
蒟蒻の醒悟

最终,在修改了232-1次后,我の眼前一绿:

又通过了一道蓝题!!!
彩蛋
闲得没事时写的手写稿:

特别感谢:Bubble_gzz
TheSky233
PS.本人第一次写题解,不喜勿喷


 浙公网安备 33010602011771号
浙公网安备 33010602011771号