BZOJ 1064 假面舞会

http://www.lydsy.com/JudgeOnline/problem.php?id=1064

思路:第一眼看的时候以为是差分约束，但是是做不了的，不过能保证的就是这题绝对是图论题。。。(废话)

分联通块考虑，如果每个联通块都是没有有向环的话，那么各个联通块中，最长链就是最大答案，3就是最小答案。

只要有一个联通块有环，那么答案一定是这个环长度的因数，最大答案，就是这些环长度的gcd

不过，要是有这个非正常的环怎么办?

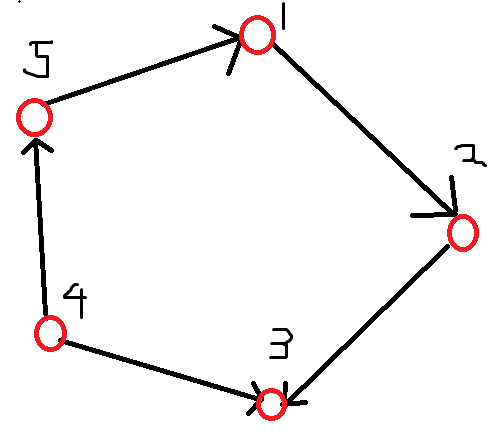
我们可以看到,4->3和2->3都指向了3，这怎么办？那么我们只要在一开始建图的时候，原来的有向边权值为1，再同时建一个反向边权值为-1，把有向图变成无向图。

为什么?，因为如图，4可以到3,2也可以到3，说明2的编号和4相同，所以2->3->4的路径实际上是"走出去一步，又走回来一步"，也就是我常说的"有来有回",按照我们刚才的建图方式，这个环的长度就是:1+1+1+1-1=3，事实上，答案也是如此，3和5编号相同，2和4编号相同，这样图中实际上是只有3种面具。

 

#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
int tot,go[2100005],next[2100005],first[2100005];
int c[200005],dis[200005],vis[200005],n,m,len,val[2100005];
int read(){
    int t=0,f=1;char ch=getchar();
    while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
    while ('0'<=ch&&ch<='9'){t=t*10+ch-'0';ch=getchar();}
    return t*f;
}
void insert(int x,int y,int z){
    tot++;
    go[tot]=y;
    next[tot]=first[x];
    first[x]=tot;
    val[tot]=z;
}
void add(int x,int y){
    insert(x,y,1);insert(y,x,-1);
}
int gcd(int a,int b){
    if (b==0) return a;
    else return gcd(b,a%b);
}
int bfs(int x){
    int h=1,t=1;c[1]=x;vis[x]=1;dis[x]=0;
    int mxdis=0,mndis=0;
    while (h<=t){
        int now=c[h++];
        for (int i=first[now];i;i=next[i]){
            int pur=go[i];
            if (vis[pur]){
                len=gcd(len,val[i]+dis[now]-dis[pur]);
                continue;
            }
            vis[pur]=1;
            c[++t]=pur;
            dis[pur]=dis[now]+val[i];
            mxdis=std::max(mxdis,dis[pur]);
            mndis=std::min(mndis,dis[pur]);
        }
    }
    return mxdis-mndis+1;
}
int main(){
    n=read();m=read();
    for (int i=1;i<=m;i++){
        int x=read(),y=read();
        add(x,y);
    }
    int sum=0;
    for (int i=1;i<=n;i++)
     if (!vis[i]) sum+=bfs(i);
    len=std::abs(len);
    if (len){
        if (len<3) {
            printf("-1 -1\n");
            return 0;
        }
        printf("%d ",len);
        for (int i=3;i<=len;i++)
         if (len%i==0) {
                printf("%d\n",i);
                break;
         }
        return 0;
    }else
    if (sum<3){
        printf("-1 -1\n");
        return 0;
    }else{
        printf("%d 3\n",sum);
        return 0;
    }
}