算法学习日记(二)---递归(上)
一、基本概念
递归,就是在运行的过程中调用自己。一个函数调用其自身,就是递归。
二、作用
1、代替多重循环
2、解决本来就是递归定义的问题
3、将问题分解为规模更小的子问题进行求解
三、递归过程
以下列递归函数为例:
public static int Factorial(int n){
if(n == 0)
return 1;
else
return n*Factorial(n-1);
}
以为Factorial(4)例,函数执行用栈表示如下:

Factorial(4)执行过程如下:
开始:Factorial(4) --> 4*Factorial(3) --> 3*Factorial(2) --> 2*Factorial(1) --> 1*Factorial(0) -->1*Factorial(0)返回 1*1 --> 2*Factorial(1)返回 2*1 --> 3*Factorial(2)返回 3*2 --> 4*Factorial(3)返回 4*6 --> 返回最终结果24.
四、例题
1、汉诺塔
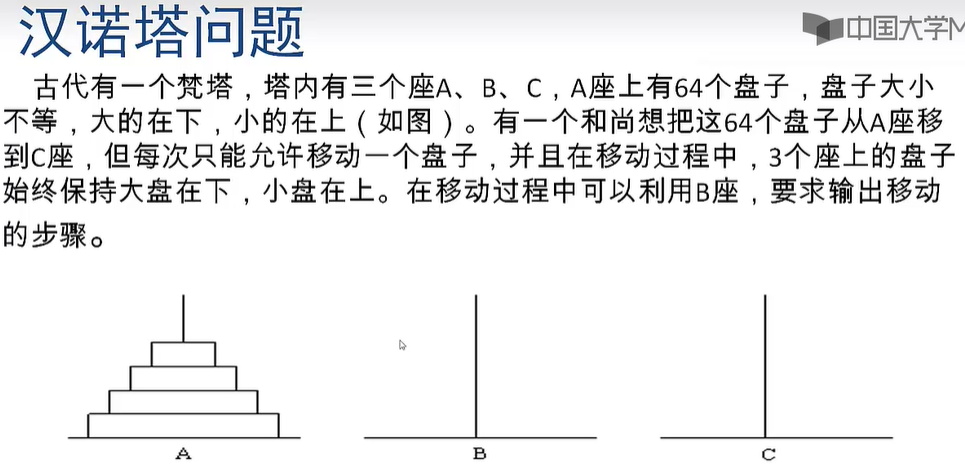
解题思路:
移动盘子过程如下:
(1)从A移动n-1个盘子到B;
(2)从A移动第n个盘子到C;
(3)从B移动n-1个盘子到C;
使用递归实现,
递归程序出口为n<=1;
题解代码:
public static void Hanoi(int n,char src,char mid,char dest){
if (n == 1){
//只需移动一个盘子
System.out.println(src+"->"+dest);
return;
}
Hanoi(n-1,src,dest,mid); //(1)先将n-1个盘子从src移动到mid
System.out.println(src+"->"+dest);//(2)在将一个盘子从src移动到dest
Hanoi(n-1,mid,src,dest); //(3)最后将n-1个个盘子从mid移动到dest
return;
}
以四个盘子为例,测试:
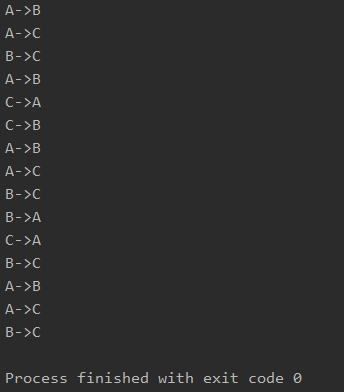
2、N皇后问题


皇后不会相互攻击的条件:即任意两个皇后都不能处于同一行、同一列或同一斜线上。
解题思路:
如果用枚举法,N皇后需要穷举NN种情况,到8皇后需要尝试88=16,777,216种情况,数量太过庞大,显然穷举法不是一种很好的解法,浪费了太多的计算资源在各种无用功上面。
对于N皇后问题,递归法是一种不错的解法,思路如下:
当我们选择了第一个皇后的位置之后,与其处于同行同列同斜线的位置便都无法被选择,第二个皇后只能放在未被第一个皇后所辐射到的位置上,接着放置第三个皇后,同样不能放在被前两个皇后辐射到的位置上,第四个皇后同样不能放在被前三个皇后辐射的位置上......若放置第N个皇后的时候,已经没有位置可选,则回退,重新放置N-1个皇后的位置。
使用递归回溯,每一次寻找下一个皇后作为递归过程,递归程序出口为每遍历完N行后。
题解代码:代码分成三个部分,第一部分寻找位置摆放皇后(find_Queen),第二部分检查该位置是否可以摆放(check),第三部分打印摆法(print)。
public class Ex_3 {
//摆放皇后
public static void find_Queen(int row,int N,int[][]Queen){
if (row > N-1){
print_queen(Queen,N);
return;
}
for (int column = 0;column < N;column++){
if (check(Queen,row,column,N)){
Queen[row][column] = 1;
//找下一个皇后
find_Queen(row+1,N,Queen);
}
//位置不符,重新找上一个皇后
Queen[row][column] = 0;
}
}
//检查是否有位置
public static boolean check(int[][] Queen,int row,int column,int N){
//检查列
for (int i = 0;i < row;i++)
if (Queen[i][column] == 1)
return false;
//检查主对角线
for (int i = row-1,j = column-1;i >= 0 && j >= 0;i--,j--)
if (Queen[i][j] == 1)
return false;
//检查副对角线
for (int i = row-1,j = column+1;i < N && i >= 0 && j < N && j >= 0;i--,j++)
if (Queen[i][j] == 1)
return false;
return true;
}
//打印皇后
public static void print_queen(int[][] Queen,int N){
for (int[] arr:Queen) {
for (int a : arr) {
System.out.print((a == 1 ? "●" : "○")+" ");
}
System.out.println();
}
System.out.println("--------");
Queen = null;
Queen = new int[N][N];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("请输入N");
int N = sc.nextInt();
int[][]Queen = new int[N][N];
find_Queen(0,N,Queen);
}
}
测试如下:
4皇后:
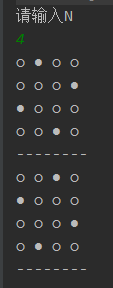
8皇后(部分):

3、逆波兰表达式



注:实际逆波兰表达式是运算符在后面,这里以题目为准
递归终止条件为:最终返回的值是一个数
每次递归即为求一次二元运算,先读取运算符,然后读取两个逆波兰表达式,如果逆波兰表达式不是一个值,继续递归一次二元运算。
题解代码:
public class Ex_4 {
private static String[] s;
private static int index = -1;
public static double exp(){
index++;
switch (s[index]){
case "+": return exp() + exp();
case "-": return exp() - exp();
case "*": return exp() * exp();
case "/": return exp() / exp();
default: return Double.valueOf(s[index]);
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
s = new String[20];
s = sc.nextLine().split(" ");
System.out.println(exp());
}
}
测试:
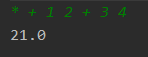



 浙公网安备 33010602011771号
浙公网安备 33010602011771号