ST表

前置知识：对数及换底公式^[1]

简介

ST 表是一种可以做到 \(\mathcal{O}(n\log n)\) 预处理 \(\mathcal{O}(1)\) 查询 RMQ 问题的数据结构。
RMQ 问题（Range Maximum/Minimum Query）即为求区间最大/小值的问题。

模板：P3865 【模板】ST 表

本题中，我们有 \(m\) 次询问，每次需求出 \([l,r]\) 的最大值。
暴力做法就是每次读入区间后搜扫一遍，显然会超时。
题目中明确指出查询复杂度应为 \(\mathcal{O}(1)\)，所以我们要使用 \(ST\) 表。

思想

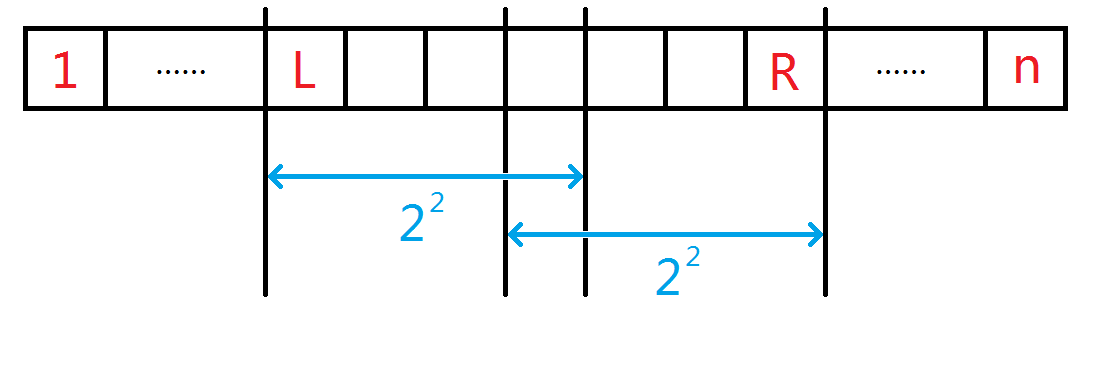
\(ST\) 表基于倍增的思想，也就是说，我们需要预处理出每个点 \(i\) 向后 \(2^j-1\) 范围（即从 \(i\) 开始的 \(2^j\) 个数）内的最大值（记为\(f_{i,j}\)）。而处理答案时，我们发现 \(\forall\,l,r(l\le r)\)，总 \(\exist\,k，[i,i+2^k-1]\bigcup\,[j-2^k+1,j] = [i,j]\)，且这个 \(k\) 满足 \(2^k\le r-l+1 < 2^{k+1}\)，即 \(k=\left\lfloor\log_{2}{(r-l+1)}\right\rfloor\)。所以，我们就可以使用 \(f\) 数组表示任意区间内元素的最大值了。

代码

• 预处理
  预处理部分，我们预处理出 \(f\) 数组，显然 \(f_{i,j}=\begin{cases}a_i&j=0\\\max(f_{i,j-1},f_{i+2^{j-1}\;,\;j-1})&otherwise\end{cases}\)，即将 \([i,i+2^j-1]\) 区间内的最大值分为 \([i,i+2^{j-1}-1]\) 和 \([i+2^{j-1},i+2^j-1]\) 两个区间来二分计算。
• 查询
  查询部分，我们根据 \(k=\left\lfloor\log_{2}{r-l+1}\right\rfloor\) 计算出 \(k\) 直接求值即可，\(k\) 可以预处理出来（\(\left\lfloor\log_{2}{r-l+1}\right\rfloor = (int) \dfrac{\ln(r-l+1)}{\ln2} = (int) \dfrac{\log(r-l+1)}{\log(2)}\)，此处 \(\ln\) 指自然对数，\(log(x)\) 指 cmath 库中的函数，默认以 \(e\) 为底）。

代码

#include<iostream>
#include<cstdio>
#include<cmath>
#define maxn 100005
using namespace std;
int n,m,a[maxn],l,r;
int f[maxn][20],k[maxn];
void set(){
	for(int i=1;i<=n;i++) { f[i][0]=a[i]; k[i]=log(i)/log(2);}
	for(int dis=1;dis<=log(n)/log(2)+1;dis++)
		for(int i=1;i+(1<<dis)-1<=n;i++) 
			f[i][dis]=max(f[i][dis-1],f[i+(1<<(dis-1))][dis-1]);
	return;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	set();
	for(int i=1;i<=m;i++){
		scanf("%d%d",&l,&r);
		printf("%d\n",max(f[l][k[r-l+1]],f[r-(1<<k[r-l+1])+1][k[r-l+1]]));
	}
	return 0;
}

---

1. 对数：若 \(a^x = N(a>0,a\neq 1)\)，则称 \(x\) 为以 \(a\) 为底 \(N\) 的对数，记作 \(x=\log_{a}{N}\)。
   换底公式：\(\log_{a}{b} = \dfrac{\log_{c}{b}}{\log_{c}{a}}(a,c>0,a,c\neq1,b>0)\)
   使用换底公式的原因是 C++ 自带的 \(\log\) 函数以 \(e\) 为底（虽然好像有以 2 为底的 \(log2\) 函数）

   ↩︎