数论分块

引入：UVA11526 H(n)

假设我们要求 \(\sum\limits_{i=1}^{n}{\left\lfloor\dfrac{n}{i}\right\rfloor}\) （n 为常数）的值，应该怎么办呢？
显然，我们可以枚举，在 \(\mathcal{O}(n)\) 复杂度内得到答案，但是，如果题目数据很大，应该如何计算呢？

数论分块

如图，假设 \(n=10\)，令 \(f(x)=\left\lfloor\dfrac{n}{x}\right\rfloor\)，作出图像，取 \(x=1\sim n\) 时图像上的点，\(\sum\limits_{i=1}^{n}{\left\lfloor\dfrac{n}{i}\right\rfloor}\) 即为这些点纵坐标之和。

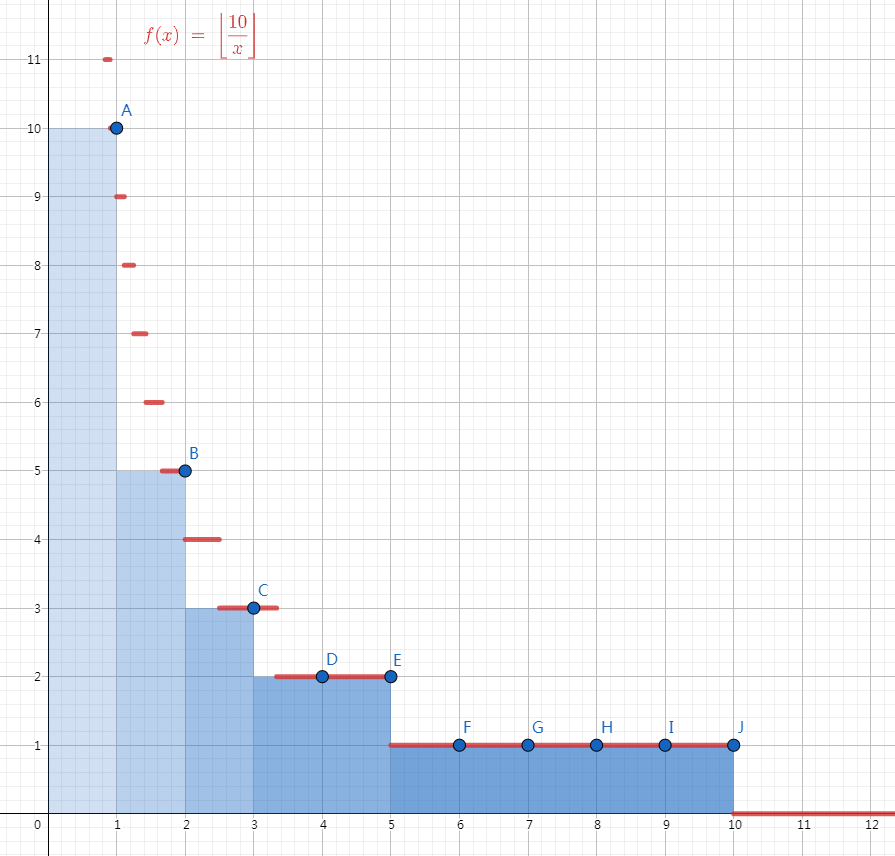
我们发现，在一定范围内，\(\left\lfloor\dfrac{n}{x}\right\rfloor\) 的图像是一段直线，于是我们可以考虑分块：将 \(\left\lfloor\dfrac{n}{i}\right\rfloor\) 相同的分为一块，则在 n=10 时我们将图分为 5 块，如上图，假设一块的左右端点为 \([l_i,r_i]\)，则这一块的答案为 \((r_i-l_i+1)\times\left\lfloor\dfrac{n}{l}\right\rfloor\)。也就是说，我们要求的式子可以发生转化：

\[\sum\limits_{i=1}^{n}{\left\lfloor\dfrac{n}{i}\right\rfloor} = \sum\limits_{i}{(r_i-l_i+1)*\left\lfloor\dfrac{n}{l}\right\rfloor} \]

于是，我们问题变成了如何求每次的 \(r_i\)。
现在给出结论：i 所在块的右端点为 \(\left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor\)，即满足 \(\left\lfloor\dfrac{n}{i}\right\rfloor=\left\lfloor\dfrac{n}{j}\right\rfloor\) 的 j 最大为 \(\left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor\)。证明如下：

• 引理：对于所有使得 \(\left\lfloor\dfrac{n}{x}\right\rfloor\) 相等的 x 的集合一定是一段连续的整数区间 [l,r]。
  证明：
  假设不是一段连续的区间，那么一定有至少一个 \(t\in(l,r)\) 使得 \(\left\lfloor\dfrac{n}{l}\right\rfloor=\left\lfloor\dfrac{n}{r}\right\rfloor\) 且 \(\left\lfloor\dfrac{n}{l}\right\rfloor\neq\left\lfloor\dfrac{n}{t}\right\rfloor\)
  \(\because t > l\quad\therefore\left\lfloor\dfrac{n}{t}\right\rfloor\le\left\lfloor\dfrac{n}{l}\right\rfloor\)
  又 \(\because t < r\quad\therefore\left\lfloor\dfrac{n}{t}\right\rfloor\ge\left\lfloor\dfrac{n}{r}\right\rfloor\)
  而 \(\left\lfloor\dfrac{n}{l}\right\rfloor=\left\lfloor\dfrac{n}{r}\right\rfloor\) 且 \(\left\lfloor\dfrac{n}{l}\right\rfloor\neq\left\lfloor\dfrac{n}{t}\right\rfloor\)，与上述结论矛盾，该假设不成立。
  \(\therefore\;\)对于所有使得 \(\left\lfloor\dfrac{n}{x}\right\rfloor\) 相等的 x 的集合一定是一段连续的整数区间 [l,r]。
• 引理2：若 \(\left\lfloor\dfrac{n}{i}\right\rfloor = k\)，则 \(n=ki+p\ (0\le p<i)\)
  证明：
  又向下取整的定义：\(\dfrac{n}{i} = \left\lfloor\dfrac{n}{i}\right\rfloor + r\ (0\le r < 1)\)
  即 \(\dfrac{n}{i} = k + r\ (0\le r < 1)\)
  则 \(n = ki + ri\ (0\le r < 1)\)
  即 \(n = ki + p\ (0\le p<i)\)
• 证明 Part1：证明 \(\left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor\) 与 \(i\) 在一块内，即 \(\left\lfloor\dfrac{n}{i}\right\rfloor=\left\lfloor\dfrac{n}{\left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor}\right\rfloor\)。
  证明：
  令 \(j = \left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor\)，\(\left\lfloor\dfrac{n}{i}\right\rfloor = k\)。
  \(\because j = \left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor = \left\lfloor\dfrac{n}{k}\right\rfloor\quad\therefore n = kj + p\ (0\le p < j)\)（引理 2）
  \(\therefore j = \dfrac{n-p}{k}\ (0\le p < j)\quad\therefore \dfrac{n}{j} = \dfrac{nk}{n-p}\ge\dfrac{nk}{n} = k\ (0\le p < j)\)，即 \(\dfrac{n}{j}\ge k\)
  若 \(\dfrac{n}{j}\ge k+1\)，则 \(\therefore n\ge kj+j\quad\therefore kj\le n-j\quad\)
  又 \(\because kj = n-p\ (0\le p < j)\)，与上述假设不符，故该假设错误。
  \(\therefore k\le \dfrac{n}{j} < k+1\quad\therefore\left\lfloor\dfrac{n}{j}\right\rfloor = k\)，即 \(\left\lfloor\dfrac{n}{i}\right\rfloor=\left\lfloor\dfrac{n}{\left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor}\right\rfloor = k\)。
• 证明 Part2：证明 \(j=\left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor\) 最大
  证明：
  证明 \(j=\left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor\) 最大即证明 \(i\le j\)；
  \(i=\left\lfloor i\right\rfloor = \left\lfloor\dfrac{n}{\frac{n}{i}}\right\rfloor\le\left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor = j\)，得证。

至此，我们就完成了数论分块的证明。
对于给定的 n，在 \(i\in[1,\left\lfloor\sqrt{n}\right\rfloor]\) 时，\(\left\lfloor\dfrac{n}{i}\right\rfloor\) 最多只有 \(\left\lfloor\sqrt{n}\right\rfloor\) 种取值，而 \(i\in(\left\lfloor\sqrt{n}\right\rfloor,n]\) 时，显然最多也只有 \(\left\lfloor\sqrt{n}\right\rfloor\) 种取值，则至多 \(2\left\lfloor\sqrt{n}\right\rfloor\) 种取值，最终复杂度在 \(\mathcal{O}(\sqrt{n})\)。

题目

例题1：UVA11526 H(n)

根据刚刚的结论模拟即可。
代码不知道对不对

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
ll T,n;
ll H(int n){
	ll ans=0;
	for(ll l=1;l<=n;){
		ll r=n/(n/l);
		ans+=(r-l+1)*(n/l);
		l=r+1;
	}
	return ans;
}
int main(){
	scanf("%lld",&T);
	while(T--){
		scanf("%lld",&n);
		printf("%lld\n",H(n));
	}
	return 0;
}

例题2：P2261 [CQOI2007]余数求和

\[\begin{aligned} G(n,k)&=\sum\limits_{i=1}^{n}{k \bmod i}\\ &=\sum\limits_{i=1}^{n}{(k-\left\lfloor\dfrac{k}{i}\right\rfloor\times i)}\\ &=nk-\sum\limits_{i=1}^{n}{\left\lfloor\dfrac{k}{i}\right\rfloor\times i}\\ &=nk-\sum\limits_{i}{(\left\lfloor\dfrac{k}{l_i}\right\rfloor\times\sum\limits_{j=l_i}^{r_i}{j})}\\ &=nk-\sum\limits_{i}{(\left\lfloor\dfrac{k}{l_i}\right\rfloor\times\dfrac{(l_i+r_i)\times(r_i-l_i+1)}{2})} \end{aligned} \]

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
ll T,n,k;
ll ans=0;
int main(){
	scanf("%lld%lld",&n,&k);
	for(ll l=1;l<=n;){
		ll r=(k/l)?min(k/(k/l),n):n;
		ans+=(r-l+1)*(l+r)/2*(k/l);
		l=r+1;
	}
	printf("%lld",n*k-ans);
	return 0;
}