Educational Codeforces Round 122 题解
A. Div. 7
数学 \(\color{white}.\) 暴力
大意
给定整数 n,改变最少的数码使得它变成 7 的倍数,输出任意一解。
思路
不难想到,由于\(x\bmod7\)的结果有且只有 7 种,所以在连续 10 个数中至少有 1 个数被 7 整除。所以,我们一定可以只改变最后一位数码,使得得到的数被 7 整除。枚举即可。
代码
#include<iostream>
#include<cstdio>
using namespace std;
int T,n;
int main(){
scanf("%d",&T);
while(T--){
scanf("%d",&n);
if(n%7==0) printf("%d\n",n);//已经被7整除
else if((n/10)==((n-n%7)/10)) printf("%d\n",n-n%7);//比它小的7的倍数只用改变1位数码
else printf("%d\n",n-n%7+7);//比它大的7的倍数只用改变1位数码
}
return 0;
}
B. Minority
字符串 \(\color{white}.\) 贪心
大意
给定 1 个 01 串,一个子串的价值是子串中较少的字符的个数(若 0 和 1 的个数相同则价值为 0)。输出所有子串的价值的最大值。
思路
显然,选择整个字符串的价值最大。但是如果整个字符串的 0 和 1 数量相同就不能选择整个字符串,此时我们考虑选择除了头(或者尾),此时价值最大,整个串中 0 或 1 的数量减 1。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 200005
using namespace std;
int T;
char a[maxn];
int main(){
scanf("%d",&T);
while(T--){
int zero=0,one=0;
cin>>a;
for(int i=0;i<strlen(a);i++){
if(a[i]=='0') zero++;
else one++;
}
if(zero==one) printf("%d\n",zero-1);
else printf("%d\n",(zero<one?zero:one));
}
return 0;
}
C. Kill the Monster
模拟 \(\color{white}.\) 数学
大意
一个游戏中,若我方角色的生命值为 \(h_C\),攻击力为 \(d_C\);对手角色的生命值为 \(h_M\),攻击力为 \(d_M\),双方进行一场战斗时,过程如下:
- 我方攻击对方,对方生命值减少 \(d_C\);
- 对方攻击我方,我方生命值减少 \(d_M\);
- 我方攻击对方,对方生命值减少 \(d_C\);
- 对方攻击我方,我方生命值减少 \(d_M\);
- ……
重复上述过程直到有一方生命值为 0 或负数,那一方就输了。
现在我方角色生命值为 \(h_C\),攻击力为 \(d_C\);对手角色的生命值为 \(h_M\),攻击力为 \(d_M\)。且我方角色有 k 枚金币,每枚金币能永久提升 w 点战斗力或 a 点生命值。求我方能否打败对方。
思路
首先我们分析战斗的过程:显然我方击败对方需要 \(t_C=\left\lceil\dfrac{h_M}{d_C}\right\rceil\) 次攻击,对方击败我方需要 \(t_M=\left\lceil\dfrac{h_C}{d_M}\right\rceil\) 次攻击。所以,若 \(t_C\le t_M\),我方获胜;若 \(t_C > t_M\),对方获胜。
然后我们发现题目中这句话:The sum of k over all test cases does not exceed 2*10^5.,也就是 \(\sum k\le 10^5\),k 的值很小,所以我们可以暴力枚举有多少金币用来提升攻击力,剩下的用来提升生命值(显然金币全部用了最好),用上述方法判断就行。
记得开 long long。
代码
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
ll T;
ll hc,dc,hm,dm,k,w,a;
int main(){
scanf("%lld",&T);
while(T--){
scanf("%lld%lld%lld%lld%lld%lld%lld",&hc,&dc,&hm,&dm,&k,&w,&a);
hc-=a;dc+=(k+1)*w;
bool flag=0;
for(ll i=0;i<=k;i++){
hc+=a;dc-=w;//枚举
if((hm/dc+(hm%dc?1:0))<=(hc/dm+(hc%dm?1:0))){
printf("YES\n");
flag=1;
break;
}
}
if(!flag) printf("NO\n");
}
return 0;
}
D. Make Them Equal
BFS \(\color{white}.\) DP \(\color{white}.\) 背包 \(\color{white}.\) 贪心
大意
有一长度为 n 的数组 a,初始每个元素均为 1。可以进行最多 k 次操作,每次操作能选择 \(i\in[1,n]\) 和 \(x\in \N^*\),使得 \(a_i = a_i + \left\lfloor\dfrac{a_i}{x}\right\rfloor\)。当 \(a_i = b_i\) 时,就能得到 \(c_i\) 的金币。求能得到金币的最大值。
思路
首先我们可以预处理出从 1 到 \(i\) 最少需要多少次操作(记为 \(dis_i\))。此时可以用 BFS 或 DP。这里使用 DP 做法。开始时令 \(dis_i = \begin{cases}0&i = 1\\ \infty&otherwise\end{cases}\)。之后暴力枚举 i,更新\(dis_j = \min(dis_i + 1,dis_j),j=i+\left\lfloor\dfrac{i}{x}\right\rfloor,x\in[1,i]\)(因为 \(x>i\)时,\(\left\lfloor\dfrac{i}{x}\right\rfloor=0\),相当于浪费了一次操作)。
此时题目就变成了:有 n 个数,k 次操作,使用 \(dis_{b[i]}\) 次操作可以获得 \(c_i\) 的金币,求获得金币的最大值。这就是最标准的 01 背包问题,套模板即可。
但是,此时复杂度为 \(O(tnk)\),理论上会 TLE(但是我交上去并没有),此时就需要进行优化。注意到 dis 数组的最大值只有 12,所以最多只需要 \(12*n\) 次操作就可以拿到所有金币,所以若 \(k\ge 12*n\),直接输出 \(\sum\limits_{i\in[1,n]}{c_i}\) 即可,或者像我一样将 k 赋值为 \(12*n\)。
总用时:\(43.70s\rightarrow 831ms\);单测试点最大用时:\(1.72s\rightarrow46ms\)
代码
- 优化前
#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 1005
#define maxk 1000005
#define inf 1e5
using namespace std;
int t,n,k;
int b[maxn],c[maxn],dis[maxn];
int f[maxk];
int main(){
for(int i=1;i<=1000;i++) dis[i]=inf;dis[1]=0;
for(int i=1;i<=1000;i++){
for(int j=1;j<=i;j++){
dis[i+i/j]=min(dis[i+i/j],dis[i]+1);
}
}
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&b[i]);
for(int i=1;i<=n;i++) scanf("%d",&c[i]);
memset(f,0,sizeof(f));
for(int i=1;i<=n;i++){
for(int j=k;j>=dis[b[i]];j--){
f[j]=max(f[j],f[j-dis[b[i]]]+c[i]);
}
}
printf("%d\n",f[k]);
}
return 0;
}
- 优化后
#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 1005
#define maxk 1000005
#define inf 1e5
using namespace std;
int t,n,k;
int b[maxn],c[maxn],dis[maxn];
int f[maxk];
int main(){
for(int i=1;i<=1000;i++) dis[i]=inf;dis[1]=0;
for(int i=1;i<=1000;i++){
for(int j=1;j<=i;j++){
dis[i+i/j]=min(dis[i+i/j],dis[i]+1);
}
}
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&k);
k=min(12*n,k);
for(int i=1;i<=n;i++) scanf("%d",&b[i]);
for(int i=1;i<=n;i++) scanf("%d",&c[i]);
memset(f,0,sizeof(f));
for(int i=1;i<=n;i++){
for(int j=k;j>=dis[b[i]];j--){
f[j]=max(f[j],f[j-dis[b[i]]]+c[i]);
}
}
printf("%d\n",f[k]);
}
return 0;
}
E. Spanning Tree Queries
数学 \(\color{white}.\) 最小生成树 \(\color{white}.\) 二分查找 \(\color{white}.\) 图论 \(\color{white}.\) 排序
大意
有一有 n 个节点和 m 条边的加权连通无向图。有 k 次询问,每次给出一个整数 \(q_i\),求所有生成树中 \(\sum\limits_{j=1}^{ n-1}|w_j-q_i|\)(\(w_j\) 为生成树各边的权值)的最小值。输出各次询问答案的异或和。
思路
我们先思考暴力的思路:也就是每次读入时计算每条边的权值,然后 Kruskal 即可,但是这样显然复杂度太高。于是我们思考,可不可以少进行几次算法呢?
我们发现,对于固定的 \(w_1\) 与 \(w_2\),改变 q 的值时,\(|w_1-q|\) 和 \(|w_2-q|\) 的大小关系不总是会改变。比如说,我们取 \(w_1 = -3,w_2 = 1\) 进行模拟,画出 \(y=|x-q|\) 的函数图像,在 x=-3 和 x=1 时取函数上的点 A 和 B。我们发现有 \(\begin{cases}|w_1-q|<|w_2-q|&q\in(-\infty,-1)\\|w_1-q|=|w_2-q|&q=-1\\|w_1-q|>|w_2-q|&q\in(-1,+\infty)\end{cases}\)(如下图)。由此,我们可以推出,\(\forall w_1,w_2(w_1 < w_2),\begin{cases}|w_1-q|<|w_2-q|&q\in(-\infty,\dfrac{w_1+w_2}{2})\\|w_1-q|=|w_2-q|&q=\dfrac{w_1+w_2}{2}\\|w_1-q|>|w_2-q|&q\in(\dfrac{w_1+w_2}{2},+\infty)\end{cases}\)。
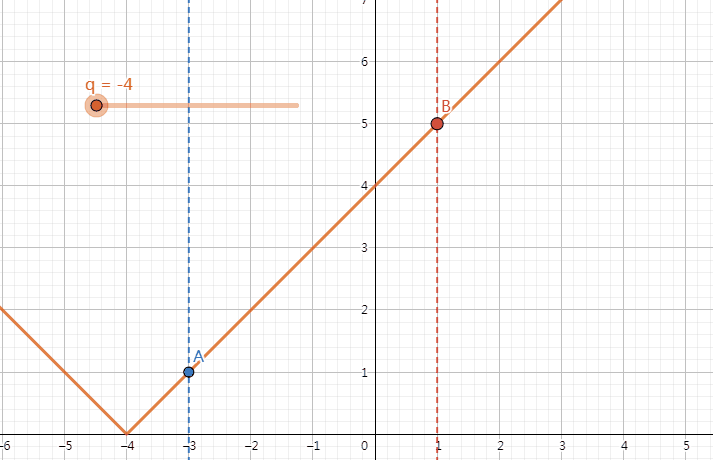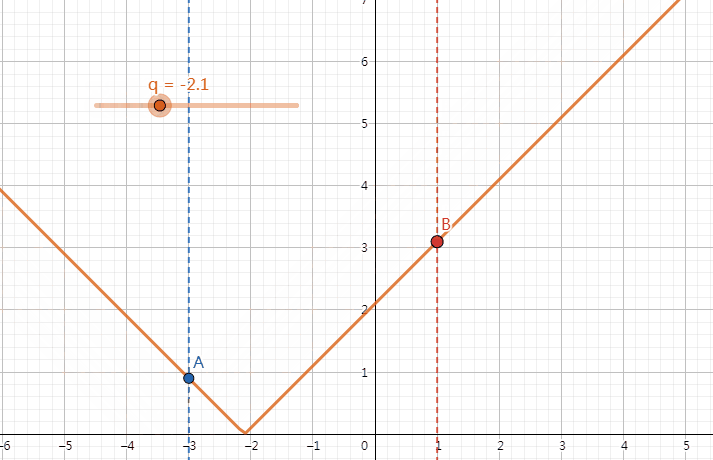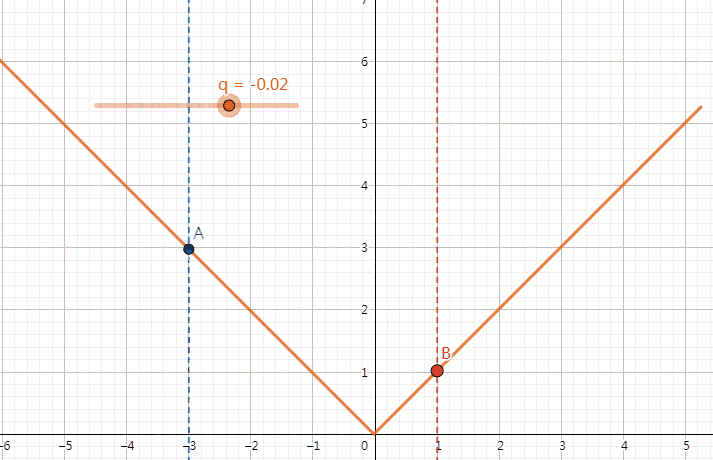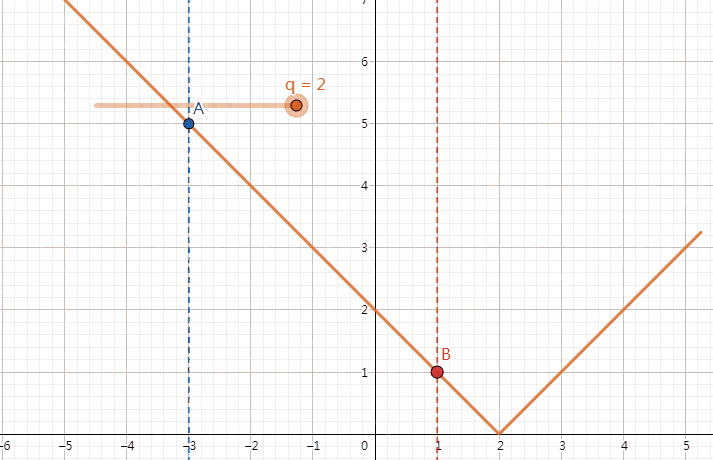
同时我们注意到,在一定范围内,q 改变时,边权的大小关系是一定的,最终结果与 q 的变化量是呈一次函数关系(因为 q+1 时,所有 \(|w_i-q|\) 对应 +1 或 -1)。因此,我们按照所有的 \(w_i\) 和所有的 \(\dfrac{w_i+w_j}{2}\) 把数轴零点分段,并计算出改变 q 时最终结果的增减量,最后输入 q 时二分查找其所在段,根据增减量处理出答案即可。
-
Q:为什么所有的 \(w_i\) 要算作零点?
-
A:如下图,我们发现,在 \((-\infty,w_i]\) 和 \([w_i,+\infty)\) 上,\(y=|w_i-q|\) 的增减性并不相同,所以为了不影响答案计算(见 \(Q\&A\ 4\)),我们将 \(w_i\) 也纳入零点中。
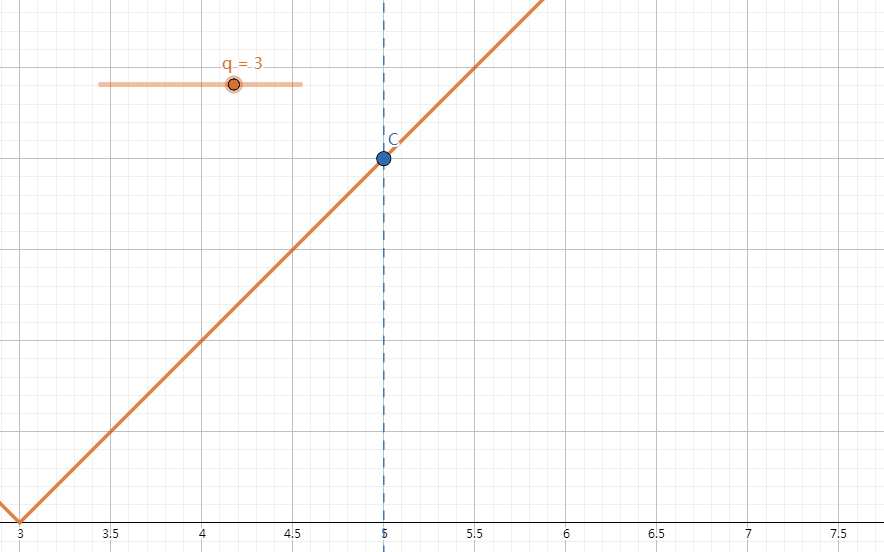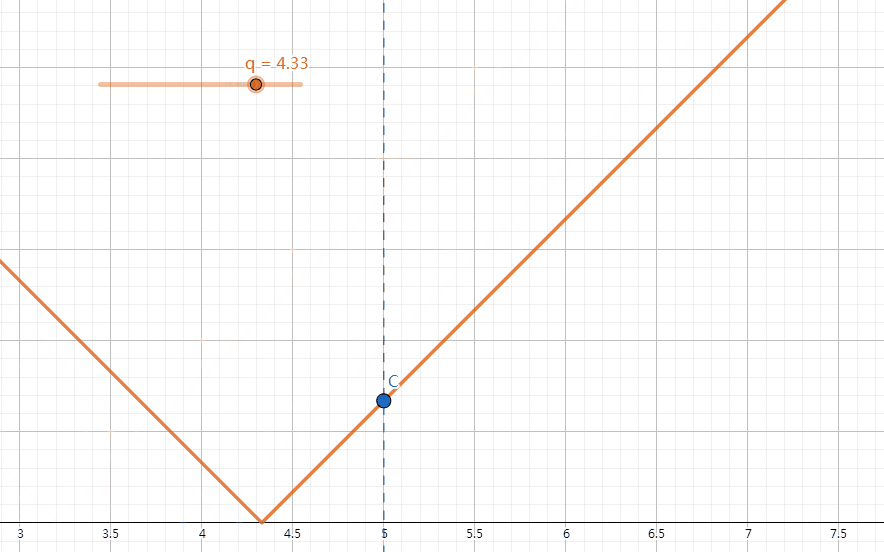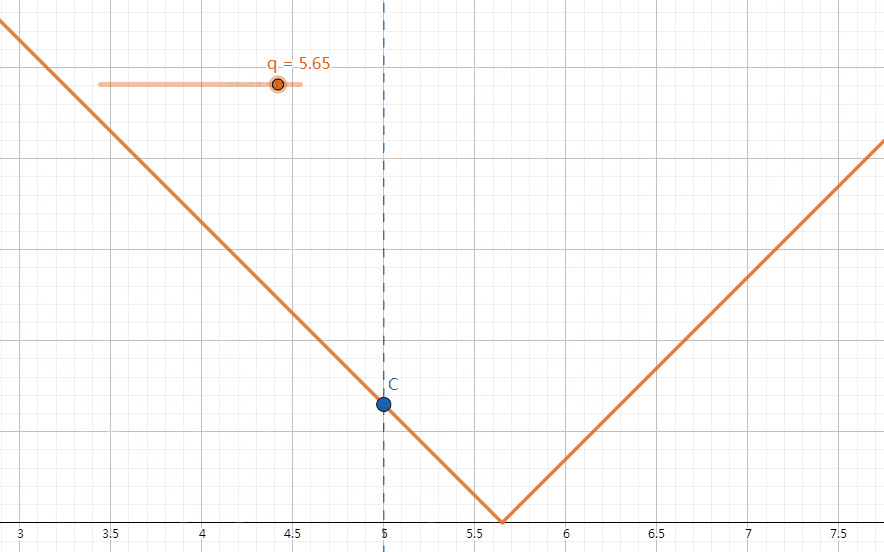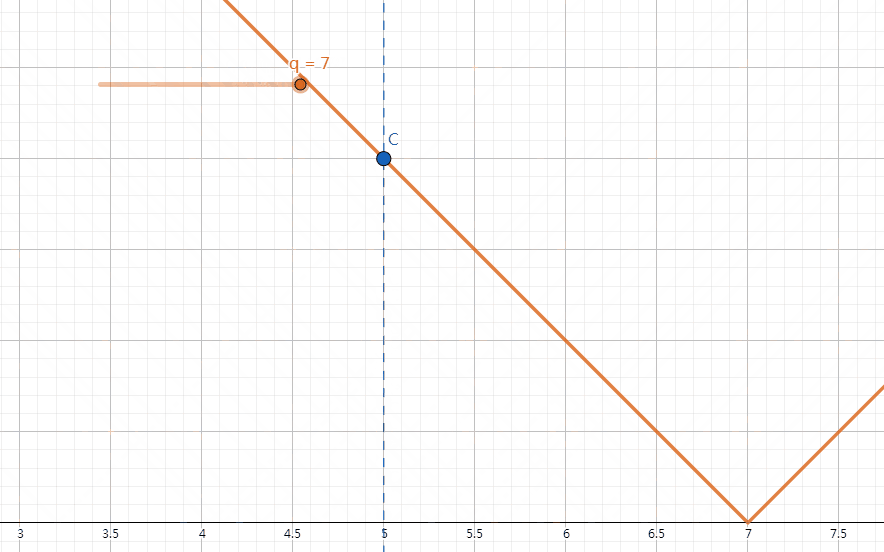
-
Q:如何计算 q 增加时有多少的 \(|w_i-q|\) 会增加?
-
A:如上图,当 \(w_i<q\) 时,\(|w_i-q|\) 随 q 增加而增大,反之亦然。所以我们只需要统计多少 \(w_i<q\) 即可。
-
Q:为什么排序这么排?
-
A:首先,第一关键字是 \(|w_i-q|\),升序排序,这是显然的。第二关键字是 \(w_i\),降序排列,使得MST选到的边多为 \(w_i>q\) 的,使得最终答案最小(原因见 \(Q\&A\ 2\And4\))。
-
Q:结果怎么算?
-
A:首先,假设二分出来的零点为 res,该零点处的 MST 答案为 \(mst_{res}.cost\),由于最终结果与 q 的变化量是一次函数关系,所以最终结果 \(=mst_{res}.cost+(\Delta q\times up-\Delta q\times(n-1-up))\)(up 为随 q 增加而增加的 \(|w_i-q|\) 数量,又由于生成树一共是 n-1 条边,固有 (n-1-up) 条边的 \(|w_i-q|\) 随 q 增加而减小)。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#define ll long long
#define maxn 55
#define maxm 305
using namespace std;
ll n,m,u[maxm],v[maxm],w[maxm],p,k,aa,bb,cc,q;
struct node{
ll from,to,dis,oridis;//两个端点、|w[i]-q|和原来的权值
}a[maxm];
struct msts{
ll cost,up;//统计零点的MST价值和q增加时有多少|w[i]-q|会增加
}mst[maxm*maxm];
ll ld[maxm*maxm],len=0;//零点
ll f[maxn];
ll aabs(ll x) {return x<0?-x:x;}
bool cmp(node aaa,node bbb) {if(aaa.dis==bbb.dis) return aaa.oridis>bbb.oridis;else return aaa.dis<bbb.dis;}
void clear() {for(ll i=1;i<=n;i++) f[i]=i;}
ll ffind(ll x) {if(f[x]==x) return x;else return f[x]=ffind(f[x]);}
ll bisearch(ll q){//二分查找所属区间
ll l=1,r=len,res=0,mid=0;
while(l<=r){
mid=(l+r)/2;
if(q<ld[mid]) r=mid-1;else {res=mid;l=mid+1;}
}
return res;
}
int main(){
//输入图的点和边
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=m;i++) scanf("%lld%lld%lld",&u[i],&v[i],&w[i]);
//处理所有零点
ld[++len]=0;
for(ll i=1;i<=m;i++){
for(ll j=i;j<=m;j++){
ld[++len]=(w[i]+w[j])/2+((w[i]+w[j])%2);//将所有端点存入数组
}
}
sort(ld+1,ld+1+len); len=unique(ld+1,ld+1+len)-ld-1;//排序+去重
//处理所有零点的MST权值和
for(ll i=1;i<=len;i++){
for(ll j=1;j<=m;j++){
a[j]=(node){u[j],v[j],aabs(w[j]-ld[i]),w[j]};
}
sort(a+1,a+1+m,cmp);
clear();
for(ll j=1;j<=m;j++){
ll r1=ffind(a[j].from),r2=ffind(a[j].to);
if(r1!=r2) {f[r2]=r1;mst[i].cost+=a[j].dis;if(a[j].oridis<=ld[i]) mst[i].up++;}
}
}
//读入并处理答案
scanf("%lld%lld%lld%lld%lld",&p,&k,&aa,&bb,&cc);
ll res,ans=0;
for(ll i=1;i<=k;i++){
if(i<=p) scanf("%lld",&q);else q=(q*aa+bb)%cc;
res=bisearch(q);//二分
ans^=(mst[res].cost+(q-ld[res])*(mst[res].up-(n-1-mst[res].up)));//答案
// printf("%d ",(mst[res].cost+(q-ld[res])*(mst[res].up-(n-1-mst[res].up))));
}
printf("%lld",ans);
return 0;
}
F. Perfect Matching
???
大意
给定一棵树,其中包含 n 个顶点(用 \(1\sim n\) 编号)和 n-1 条边(用 \(1\sim n-1\) 编号)。初始时只有节点 1 被激活。
有若干次询问,分为以下 3 种:
- 1 \(v\):激活节点 \(v\),此时确保与 \(v\) 相邻的点至少有一个被激活。输出所有被激活的点构成的一个完美匹配中边的编号之和(任意一个即可)。
- 2:此询问紧跟第 1 种询问且最多只有 10 次。升序输出所有被激活的点构成的一个完美匹配中的边的编号,必须确保输出的边的编号总和就是上一次询问输出的值。
- 3:结束程序。
本题强制在线。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号