A*算法

A*寻路算法

引入

假设你身处一座迷宫，要从起点穿过障碍到达终点，像上图一样，想要快速找到一条最短路径该如何做呢？
DFS？显然太耗时间。BFS？有太多点不必遍历。
所以，我们可以引入A*算法来解决这一问题。

概述

A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。 ----摘自 百度百科

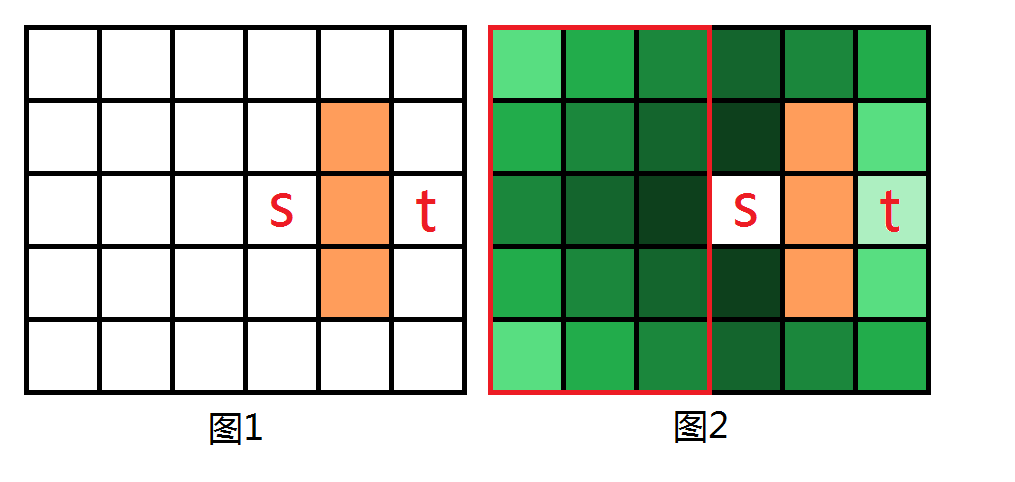
如下图1，若要搜索s到t的最短路径（只能上下左右走），用BFS的话，如图2，会搜索大量的没用格子（如红框框起来的），原因是什么呢？我们发现，是因为BFS会以自身为中心，无条件向四周蔓延。所以，我们想，能否加上若干条件，让BFS总向终点的方向搜呢？

在A* 算法中，f数组维护了“从初始状态经由状态n到目标状态的最小代价估计”，即上述的“条件”，计算方法为：\(f_{i,j}=g_{i,j}+h_{i,j}\)。其中，g数组存的是“在状态空间中从初始状态到状态n的最小代价”，h数组存了“从状态n到目标状态的路径的最小估计代价”。说人话，g存的是从起点到该点的代价，h存的是该点到终点的预计代价，f就是g+h，即综合代价。显然f越小，它在最短路径上的可能性越大，我们就要选择它继续遍历。
于是，我们得到了A* 算法的大致框架：在BFS中插入f数组预估代价，选择合适点进行搜索。

详解

准备阶段

在正式讲解之前，我们先明确f,g,h的计算方法及一些函数及变量。g是起点到该点的代价，我们可以搜索时维护步数；h是该点到终点的代价，我们有以下方式计算：曼哈顿距离、对角距离、欧几里得距离。这里只能上下左右移动，故选择曼哈顿距离来当做代价h；f数组就是g,h两数组相加。
再就是选点的过程，我们每次遍历都选择在队列里的（参照BFS）、f最小的（参照A* ）点进行遍历，这就要求我们选的存放点的数据结构能够增减点、维护最值，这里我选了set（其实优先队列priority_queue等也行）。
还有搜索中，我们要存放哪些点遍历过而哪些没有，我选用两个数组open（存在set中的点）和close（遍历过了，不用再管）存放，在下文中分别用绿色和蓝色边框表示。

开始搜索

首先，我们肯定是把起点s放入set，同时设置open[s]=1。取set中f最小的点（此时为s），设置close为1，open为0（相当于把这个点固定了，不再更新，此时其f,g,h值显然是最优的）搜相邻的可走的方格，更新它们的f,g,h值，并把它们加入队列set中。之后依次取f最小的点重复上述过程直到到了终点即可。

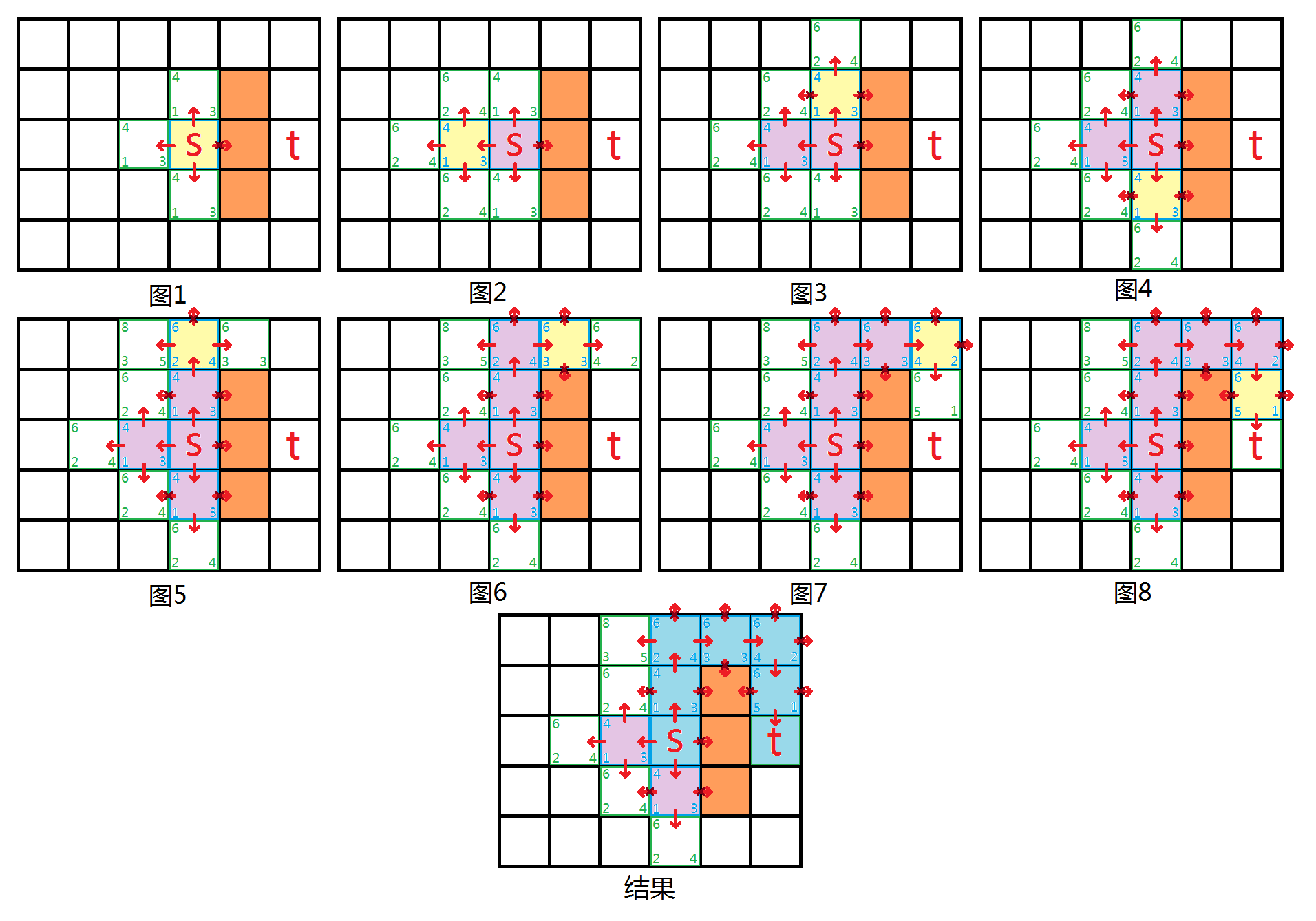
如图，底色橙色的是障碍物。绿色边框的是open中的点，蓝色的是close中的点。close中，底色淡紫色的是搜过的点，淡黄色的是在搜的点。每个点左下方的是g，右下方的是h，左上方的是f。底色淡蓝色的是最终的路径。
让我们模拟亿下。如图1，首先，拿出open中f最小的点，此时为起点s，将其设为close，并从s开始向四周搜，并将四周加入open中，更新f,g,h值。然后，从open中拿出f纸最小的点，这里s左边、上面、下面的点都满足要求，图2,3,4依次搜了这些点周围的点。之后，open中f最小为6，如图5，f一样时我们一般选最后加进来的点搜，于是依次有了图5,6,7,8，图8中到了终点。

回溯路径

图8中成功到了终点（即终点t进入了open），这时，我们如何输出路径呢？只要从终点开始沿来时的箭头一路退回去就好了。为了在程序中直接输出路径，我们可以从终点开始搜起点（我是这么做的），最后沿箭头从起点回溯到终点的路径就是从起点到终点的最短路径。

总结

所以，A* 算法的主要流程就是：

1. 将起点s加入open
2. 重复以下过程：
   • 找出open中f最小的点，将其从open转移至close中
   • 遍历其四周的方格，若能更新就更新
   • 直到open空了或者终点t进入了open就结束
3. 回溯输出路径

代码

#include<iostream>
#include<cstdio>
#include<set>
#define maxn 105
using namespace std;
int n,s1,t1,s2,t2;
int a[maxn][maxn];
int dx[5]={1,-1,0,0},dy[5]={0,0,1,-1};
bool open[maxn][maxn],close[maxn][maxn];
struct node{
	int f,g,h,x,y,fax,fay;
	//f,g,h含义如文中所述;x,y是该点坐标;fax,fay是父节点坐标 
	bool operator<(const node& xx) const {return f<xx.f;}//重载>和< 
	bool operator>(const node& xx) const {return f>xx.f;}
//	bool operator==(const node& xx) const{
//		return (f==xx.f&&g==xx.g&&h==xx.h&&x==xx.x&&y==xx.y&&fax==xx.fax&&fay==xx.fay);
//	}
//	bool operator!=(const node& xx) const{
//		return !(f==xx.f&&g==xx.g&&h==xx.h&&x==xx.x&&y==xx.y&&fax==xx.fax&&fay==xx.fay);
//	}
}s[maxn][maxn];
multiset<node> openlist;//队列 
int abs(int x) {return x<0?-x:x;}
int dis(int px1,int py1,int px2,int py2) {return abs(px1-px2)+abs(py1-py2);}//曼哈顿距离预估到终点的价值 
void astar(){
	s[s1][t1]=(node){dis(s1,t1,s2,t2),0,dis(s1,t1,s2,t2),s1,t1,-1,-1};//把起点加入队列 
	open[s1][t1]=1;openlist.insert(s[s1][t1]);
	while(openlist.size()!=0&&!open[s2][t2]){//重复直到搜到终点或把能搜的点都搜完了 
		int topx=(*openlist.begin()).x,topy=(*openlist.begin()).y;openlist.erase(openlist.begin());
		//取队首点的坐标 
		open[topx][topy]=0;close[topx][topy]=1;//从open转移到close中 
		for(int i=0;i<4;i++){//遍历四周的点 
			int newx=topx+dx[i],newy=topy+dy[i];
			if(a[newx][newy]==1||close[newx][newy]==1||newx<=0||newx>n||newy<=0||newy>n) continue;
			//不符合条件(是障碍物或搜过了或超范围) 
			if(!open[newx][newy]){//若没搜过则加入队中 
				open[newx][newy]=1;
				s[newx][newy]=(node){0,s[topx][topy].g+1,dis(newx,newy,s2,t2),newx,newy,topx,topy};
				s[newx][newy].f=s[newx][newy].g+s[newx][newy].h;
				openlist.insert(s[newx][newy]);
			}else{
				if(s[topx][topy].g+1<s[newx][newy].g){//搜过但路径更优也更新 
					openlist.erase(s[newx][newy]);
					s[newx][newy]=(node){0,s[topx][topy].g+1,dis(newx,newy,s2,t2),newx,newy,topx,topy};
					s[newx][newy].f=s[newx][newy].g+s[newx][newy].h;
					openlist.insert(s[newx][newy]);
				}
			}
		}
	}
	if(s[s2][t2].g>0){//若终点搜过了 
		int fx=s2,fy=t2,fxx=s2;
		printf("%d\nThe Path is: ",s[s2][t2].g);
		while(s[fx][fy].fax!=-1){//向前回溯输出路径 
			printf("(%d,%d)->",s[fx][fy].x,s[fx][fy].y);
			fxx=fx;fx=s[fx][fy].fax;fy=s[fxx][fy].fay;
		}
		printf("(%d,%d)-->End.",s[fx][fy].x,s[fx][fy].y);
	}else printf("-1");//终点没被搜则无解 
}
int main(){
	scanf("%d",&n);scanf("%d%d%d%d",&s1,&t1,&s2,&t2);//(s1,t1)是起点,(s2,t2)是终点 
	swap(s1,s2);swap(t1,t2);//互换起点和终点以便输出路径 
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			scanf("%d",&a[i][j]);
	astar();//计算 
	return 0;
}
/*
01网格图,从(s1,t1)到(s2,t2),1为障碍,只能上下左右走,输出最短路径.
*/
/*
6 6 1 6 5
0 0 0 1 0 0
0 1 0 0 0 0
0 1 0 1 0 1
0 1 0 1 0 0
0 1 0 0 1 0
0 1 0 1 0 0
10 8 3 2 8
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 1 0 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 1 0 0 0 0
*/