树状数组
树状数组
简介
树状数组和线段树具有相似的功能,但他俩毕竟还有一些区别:树状数组能有的操作,线段树一定有;线段树有的操作,树状数组不一定有。但是树状数组的代码要比线段树短,思维更清晰,速度也更快,在解决一些单点修改的问题时,树状数组是不二之选。--选自\(OI-WIKI\)
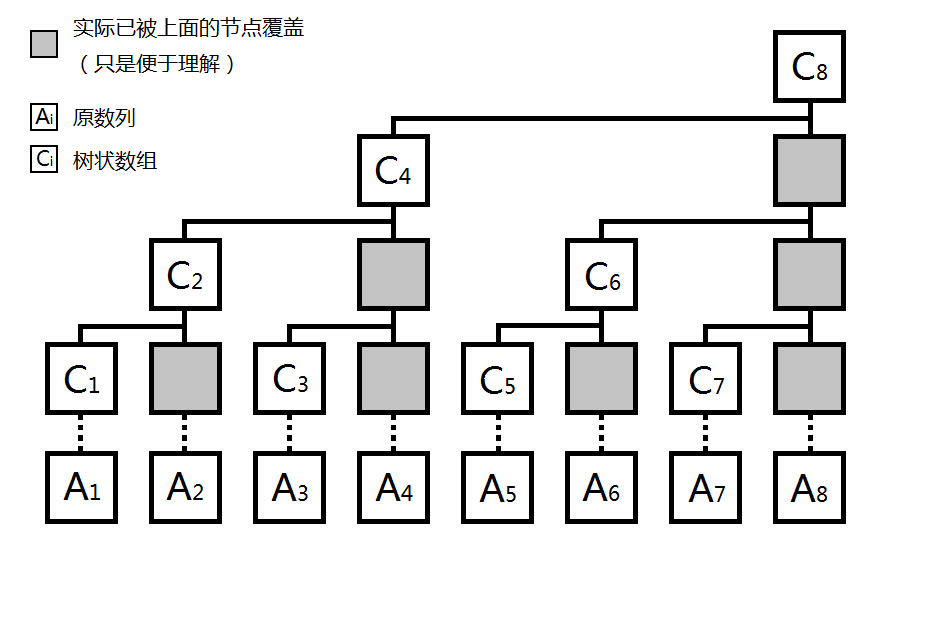
如图,\(a\)数组为原序列,\(c\)数组为树状数组,可以得到以下规律:
\(c_1=a_1\)
\(c_2=a_1+a_2\)
\(c_3=a_3\)
\(c_4=a_1+a_2+a_3+a_4\)
\(c_5=a_5\)
\(c_6=a_5+a_6\)
\(c_7=a_7\)
\(c_8=a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8\)
…
看上去没有什么规律,但是我们将下标转化为二进制以后:
\(c_{(0001)_2}=a_{(0001)_2}\)
\(c_{(0010)_2}=a_{(0001)_2}+a_{(0010)_2}\)
\(c_{(0011)_2}=a_{(0011)_2}\)
\(c_{(0100)_2}=a_{(0001)_2}+a_{(0010)_2}+a_{(0011)_2}+a_{(0100)_2}\)
\(c_{(0101)_2}=a_{(0101)_2}\)
\(c_{(0110)_2}=a_{(0101)_2}+a_{(0110)_2}\)
\(c_{(0111)_2}=a_{(0111)_2}\)
\(c_{(1000)_2}=a_{(0001)_2}+a_{(0010)_2}+a_{(0011)_2}+a_{(0100)_2}+a_{(0101)_2}+a_{(0110)_2}+a_{(0111)_2}+a_{(1000)_2}\)
这时可能就能发现有规律了,我们先引入定义:
定义:一个数\(i\)的二进制中最低位的\(1\)的位置称为\(i\)的\(lowbit\),如\(lowbit((10010110)_2)=(00000010)_2=2\),同理\(lowbit(5)=1,lowbit(6)=2,lowbit(8)=8\),也就是说,\(lowbit(i)=\min\limits_{k\in \N,2^k\mid x}{2^k}\)
那么,我们可以发现,\(c_i=\sum\limits_{x=i-lowbit(i)+1}^{i}a_x\)
\(lowbit\)的求法有很多,最常用的是:\(lowbit(i)=i\&(-i)\)
因为负数用补码存储,即将这个数的二进制取反并加\(1\),如\(10\)的二进制为\(1010\),取反得到反码\(0101\),加\(1\)得到补码\(0110\),此时\((1010)\&(0110)=0010=(2)_{10}=lowbit(10)\)。那么,对于所有的\(i\),其反码与原码相反,\(+1\)后会使最低位的原码\(1\)处的值变成\(1\),故按位与后得到\(lowbit(i)\)
- 代码
int lowbit(int x){
return x&(-x);
}
单点修改 + 区间查询
单点修改
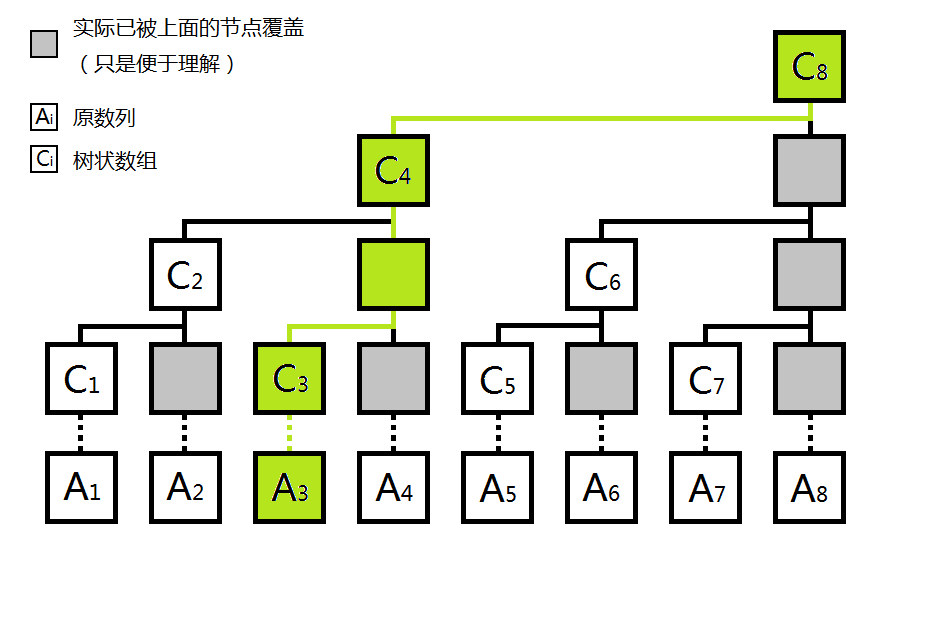
如图,假设我们要修改\(a_3\)的值,那么相应改变的有\(c_3,c_4,c_8\),我们发现\(3+lowbit(3)=4,4+lowbit(4)=8\),所以我们得到,改变\(a_i\)的值就要改变\(c_{x_1},c_{x_2},…,c_{x_n}(x_1=i,x_j=x_{j-1}+lowbit(x_{j-1}),x_j\in[1,n])\)
- 代码
void pluss(int dir,int num){ //a[dir]加上num
for(int i=dir;i<=n;i+=lowbit(i)){
c[i]+=num;
}
}
区间查询
相应的,我们可能要查询\([1,i]\)区间的值的和(后文无特殊说明外,本部分中\([l,r]\)表示\(\sum\limits_{i=l}^{r}{a_i}\)),类比前缀和,\([l,r]\)等于\([1,r]-[1,l-1]\)
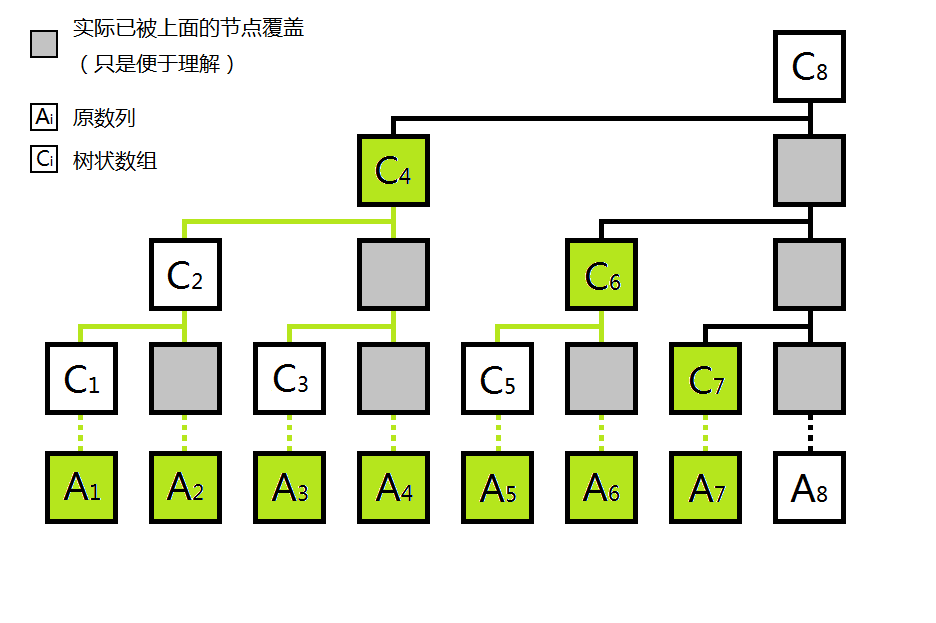
假如我们要求\([1,7]\),我们相当于是求\([1,4]+[5,6]+[7,7]\),即\(c_4+c_6+c_7\),注意到\(6=7-lowbit(7),4=6-lowbit(6)\),类比修改我们得到求区间\([1,i]\)内的值的和\([1,i]=c_{x_1}+c_{x_2}+…+c_{x_n}(x_1=i,x_j=x_{j-1}-lowbit(x_{j-1}),x_j\in[1,n])\)
- 代码
int search(int dir){
int ans=0;
for(int i=dir;i>=1;i-=lowbit(i)){
ans+=c[i];
}
return ans;
}
模板#1:P3374
- 代码
/*
c[1]=a[1]
c[2]=a[1]+a[2]
c[3]=a[3]
c[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=a[5]+a[6]
c[7]=a[7]
c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
...
c[n]=a[n-k+1]+a[n-k+2]+...+a[n] (k=lowbit(n))
sumn=c[n]+c[n-k1]+c[(n-k1)-k2]+...(ki=lowbit(n-k1-k2-...-k(i-1)))
a[n]包含于c[n+k1],c[n+k1+k2],...(ki=lowbit(n+k1+k2+...+k(i-1)))
*/
#include<iostream>
#include<cstdio>
#define maxn 500005
using namespace std;
int n,m,opt,x,y,c[maxn];
int lowbit(int x){
return x&(-x);
}
void pluss(int dir,int num){
for(int i=dir;i<=n;i+=lowbit(i)){
c[i]+=num;
}
}
int search(int dir){
int ans=0;
for(int i=dir;i>=1;i-=lowbit(i)){
ans+=c[i];
}
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&x);
pluss(i,x);
}
while(m--){
scanf("%d%d%d",&opt,&x,&y);
if(opt==1){
pluss(x,y);
}else{
printf("%d\n",search(y)-search(x-1));
}
}
return 0;
}
区间修改 + 单点查询
区间修改
此时我们引入差分,将区间修改转化为单点修改。
定义差分数组\(d\):\(d_i=a_i-a_{i-1}(i\in[1,n])\)
比如说\(a\)数组为{\(1,5,4,2,3\)},则差分数组\(d\)为{\(1,4,-1,-2,1\)}
此时若将\([2,4]\)区间内的值加\(2\),则改变后的\(a\)为{\(1,7,6,4,3\)},\(d\)为{\(1,6,-1,-2,-1\)}
此时可以发现,将\(a\)中\([2,4]\)的值加了\(2\)让\(d\)的变化为:\(d_2+2,d_5-2\),其余不变。类比一下,我们可以得出,将\([l,r]\)的值加\(k\),\(d\)数组的变化为:\(d_l+k,d_{r+1}-k\),其余不变
证明也很简单,将\([l,r]\)的值加\(k\),则\(d_l\)的值从\(a_l-a_{l-1}\)变成了\((a_l+k)-a_{l-1}\),增加了\(k\);\(d_{r+1}\)的值从\(a_{r+1}-a_r\)变成了\(a_{r+1}-(a_r+k)\),减小了\(k\);而\(\forall x\in[l+1,r]\),值从\(a_x-a_{x-1}\)变成了\((a_x+k)-(a_{x-1}+k)\),不变。
- 代码
//此时用树状数组维护差分数组d
void pluss(int dir,int num){
for(int i=dir;i<=n;i+=lowbit(i)){
d[i]+=num;
}
}
…
scanf("%d",&opt);
if(opt==1){
scanf("%d%d%d",&x,&y,&z);
pluss(x,z);
pluss(y+1,-z);
}
单点查询
由于有了差分数组,那么单点查询就非常简单了,因为\(d_i=a_i-a_{i-1}\),所以\(a_i=(a_i-a_{i-1})+(a_{i-1}-a_{i-2})+…+(a_2-a_1)+(a_1-a_0)=d_i+d_{i-1}+…+d_1\),即\(a_i=\sum\limits_{j=1}^{i}{d_j}\)
于是我们就可以用刚刚的区间查询查\([1,i]\)的值的和来求出\(a_i\)了(树状数组维护的是差分数组\(d\)!)
- 代码
int search(int dir){
int ans=0;
for(int i=dir;i>=1;i-=lowbit(i)){
ans+=d[i];
}
return ans;
}
…
scanf("%d",&opt);
if(opt==1){
…
}else{
scanf("%d",&x);
printf("%d\n",search(x));
}
模板#2:P3368
- 代码
/*
差分 d[i]=a[i]-a[i-1]
a[i]=d[1]+d[2]+...+d[i]
*/
#include<iostream>
#include<cstdio>
#define maxn 500005
using namespace std;
int n,m,opt,x,y,z,d[maxn],pre;
int lowbit(int x){
return x&(-x);
}
void pluss(int dir,int num){
for(int i=dir;i<=n;i+=lowbit(i)){
d[i]+=num;
}
}
int search(int dir){
int ans=0;
for(int i=dir;i>=1;i-=lowbit(i)){
ans+=d[i];
}
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&x);
pluss(i,x-pre);
pre=x;
}
while(m--){
scanf("%d",&opt);
if(opt==1){
scanf("%d%d%d",&x,&y,&z);
pluss(x,z);
pluss(y+1,-z);
}else{
scanf("%d",&x);
printf("%d\n",search(x));
}
}
return 0;
}
区间修改 + 区间查询
这是线段树最烦的部分,但树状数组还是轻松解决
此时,我们顺着刚刚的思路,因为要求\([1,n]\)即\(\sum\limits_{i=1}^{n}{a_i}\)的值(同上\([l,r]\)可以用\([1,r]-[1,l-1]\)求),我们先将其变形:
我们可以发现,在这个式子中\(d_1\)被加了\(n\)次,\(d_2\)被加了\((n-1)\)次,…,\(d_x\)被加了\((n-x+1)\)次,故:
所以,我们可以用树状数组维护\(\sum\limits_{i-1}^{n}{d_i}\)和\(\sum\limits_{i-1}^{n}{(d_i\times i)}\),不妨令其分别为\(sum1\)和\(sum2\),就得到了区间修改与区间查询的方法:
区间修改
同上,\(sum1\)的修改同“区间修改 + 单点查询”中数组\(d\)的修改;
\(sum2\)的修改即乘上对应的\(i\)即可
- 代码
void pluss(ll dir,ll num){
for(int i=dir;i<=n;i+=lowbit(i)){
sum1[i]+=num;
sum2[i]+=num*dir;
}
}
…
scanf("%lld",&opt);
if(opt==1){
scanf("%lld%lld%lld",&x,&y,&z);
pluss(x,z);
pluss(y+1,-z);
}
区间查询
\([1,n]\)的值的和即为\((n+1)\times\sum\limits_{i-1}^{n}{sum1_i}-\sum\limits_{i-1}^{n}{sum2_i}\)
\([l,r]\)的值的和即为\([1,r]-[1,l-1]\)
- 代码
ll search(ll dir){
ll ans=0;
for(ll i=dir;i>=1;i-=lowbit(i)){
ans+=(dir+1)*sum1[i]-sum2[i];
}
return ans;
}
…
scanf("%lld",&opt);
if(opt==1){
…
}else{
scanf("%lld%lld",&x,&y);
printf("%lld\n",search(y)-search(x-1));
}
模板#3:P3372
- 代码
/*
sum1 维护 d[i]
sum2 维护 d[i]*i
*/
#include<iostream>
#include<cstdio>
#define maxn 500005
#define ll long long
using namespace std;
ll n,m,opt,x,y,z,sum1[maxn],sum2[maxn],pre;
ll lowbit(ll x){
return x&(-x);
}
void pluss(ll dir,ll num){
for(int i=dir;i<=n;i+=lowbit(i)){
sum1[i]+=num;
sum2[i]+=num*dir;
}
}
ll search(ll dir){
ll ans=0;
for(ll i=dir;i>=1;i-=lowbit(i)){
ans+=(dir+1)*sum1[i]-sum2[i];
}
return ans;
}
int main(){
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=n;i++){
scanf("%lld",&x);
pluss(i,x-pre);
pre=x;
}
while(m--){
scanf("%lld",&opt);
if(opt==1){
scanf("%lld%lld%lld",&x,&y,&z);
pluss(x,z);
pluss(y+1,-z);
}else{
scanf("%lld%lld",&x,&y);
printf("%lld\n",search(y)-search(x-1));
}
}
return 0;
}
注:两数据结构在模板题\(P3372\)的时空比较
带有\(lazytag\)懒标优化的线段树:\(378ms\ 12.98MB\)
上述区间修改与查询的树状数组:\(163ms\ 7.00MB\)
完结撒花!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号