网络流24题 - 4
题目顺序按照洛谷“\(\color{#13C2C2}{网络流24题}\)”标签按难度排序。
题目的字体颜色为洛谷此题难度的颜色。
本人的题单: 网络流24题
P3254 \(\color{#9D3DCF}{圆桌问题}\)
题目大意
有\(m\)个单位,第\(i\)个单位派出了\(c_i\)名代表参加会议。会议共有\(n\)张圆桌,第\(i\)张圆桌最多容纳\(r_i\)人。要求每个圆桌的代表不能有来自于同一个单位的,求是否有可行方案,若有,输出任意一种。
思路
很直观地想到建立超级源点\(s\)与超级汇点\(t\),将\(s\)连向每个单位,边权为单位的人数,表示提供初始人数;每张桌子连向\(t\),边权为桌子最多容纳的人数;每个单位与每张桌子都有连边,边权为\(1\),意思是每个单位只能有最多\(1\)个人去某张圆桌(有超过一个人的话就不符合题意)。此时跑最大流,若得到的最大流等于总人数,那么说明能坐得下,否则坐不下。
细节
- 先输入单位数再输入圆桌数,且输出的是每个单位的人坐在哪些圆桌而不是每个圆桌坐了哪些单位的人。(\(\color{rgb(231,76,60)}{WA}\ \ On\ \ Test2\))
代码
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 205
#define maxm 5005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int n,m,s,t,rtot=0;
int rin[maxn],tin[maxn];
int head[maxn],tt=1;
struct node{
int to,dis,nex;
}a[maxm*2];
void add(int from,int to,int dis){
a[++tt].to=to;a[tt].dis=dis;a[tt].nex=head[from];head[from]=tt;
a[++tt].to=from;a[tt].dis=0;a[tt].nex=head[to];head[to]=tt;
}
bool vis[maxn];
int dep[maxn],cur[maxn];
bool bfs(){
for(int i=0;i<=t;i++){
vis[i]=0;
dep[i]=inf;
cur[i]=head[i];
}
queue<int> q;
vis[s]=1;
q.push(s);
dep[s]=0;
while(!q.empty()){
int top=q.front();
q.pop();
for(int i=head[top];i;i=a[i].nex){
if(dep[top]+1<dep[a[i].to]&&a[i].dis){
dep[a[i].to]=dep[top]+1;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
return dep[t]!=dep[0];
}
ll ans=0;
int dfs(int x,int minn){
if(x==t){
ans+=minn;
return minn;
}
int use=0;
for(int i=cur[x];i;i=a[i].nex){
cur[x]=i;
if(dep[a[i].to]==dep[x]+1&&a[i].dis){
int search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(bfs()){
dfs(s,inf);
}
}
void output(){
if(ans>=rtot){//==就可以了,因为最大流不会超过总人数(因为从源点出发的边权和就是总人数)
printf("1\n");
}else{
printf("0");
return;
}
for(int i=1;i<=m;i++){
for(int j=head[i];j;j=a[j].nex){
if(a[j].to>=m+1&&a[j].to<=m+n&&!a[j].dis){
printf("%d ",a[j].to-m);
}
}
printf("\n");
}
}
int main(){
scanf("%d%d",&m,&n);
s=m+n+1;
t=s+1;
for(int i=1;i<=m;i++){
scanf("%d",&rin[i]);
rtot+=rin[i];//记录总人数
}
for(int i=1;i<=n;i++){
scanf("%d",&tin[i]);
}
for(int i=1;i<=m;i++){//可以在读入时建边,不必要像这样另外写循环
add(s,i,rin[i]);//源点连单位,提供初始人数
for(int j=1;j<=n;j++){
add(i,j+m,1);//单位连每张圆桌,且每个单位最多1人坐
if(i==m){//不一定用m,只是为了防止建了很多次边
add(j+m,t,tin[j]);//圆桌连汇点,权值为最大容纳人数
}
}
}
dinic();//跑最大流
output();
return 0;
}
P4012 \(\color{#9D3DCF}{深海机器人问题}\)
题目大意
有一\((P+1)*(Q+1)\)的网格,左下角坐标为\((0,0)\),右上角坐标为\((Q,P)\),每条边上有一个物品,边权为其价值。现在有\(a\)个出生点,每个点\((x_i,y_i)\)都有\(k_i\)只机器人;还有\(b\)个撤离点,每个撤离点\((x_i,y_i)\)可以撤走(拿走)\(r_i\)只机器人。每个机器人只能从自己所在的出生点出发,沿网格线向右或上两个方向运动到任意一个撤离点离开,路过某条边时可以拿走这条边上的物品,每件物品只能拿一次,求能拿到物品的权值和最大值。下图为样例,答案为\(42\),路线如蓝色部分。
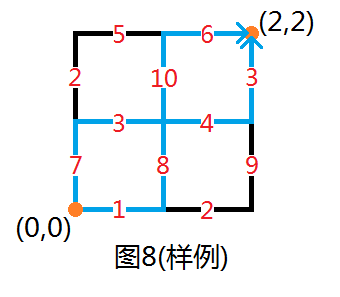
思路
显然这是道多源多汇的题目,我们可以用最大费用最大流完成:建立超级源点\(s\)连接每一个出生点\(i\),权值为\(c_i\),表示给这个出生点\(c_i\)的流量(\(1\)流量表示\(1\)个机器人),\(0\)的费用;建立超级汇点\(t\),所有撤离点都与它相连,且第\(i\)个撤离点的权值为\(r_i\),费用为\(0\),表示最多撤离\(r_i\)的机器人。对于网格中的每一个点\((i,j)\),机器人能从其走到\((i+1,j)\)和\((i,j+1)\),故连边。下面解决每件物品只能取\(1\)次的问题:我们将\((i,j)\)连两条边至\((i,j+1)\)(\((i+1,j)\)同理),一条\(f=1,c=val\)(\(val\)为物品价值),表示只能有\(1\)只机器人通过,并累加\(val\)的费用(即捡起物品);另一条边\(f=\infty,c=0\),表示其它机器人可以通过,但是不加费用。这样就解决了每条边只能捡\(1\)次的问题了。
关于点的编号,我是将所有点从下至上,从左至右编号\(1\sim (P+1)(Q+1)\)的。
细节
- 题目中说的“a行和b行输入时横纵坐标要反过来”。(\(\color{rgb(231,76,60)}{WA}\ \ On\ \ Test2\))
- 连边时点的编号注意表示清楚。
代码
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 5005
#define maxm 50005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int numbe,numde,p,q,s,t,xx,numro,dirx,diry;
int head[maxn],tt=1;
struct node{
int to,dis,cost,nex;
}a[maxm*2];
void add(int from,int to,int dis,int cost){
a[++tt].to=to;a[tt].dis=dis;a[tt].cost=cost;a[tt].nex=head[from];head[from]=tt;
a[++tt].to=from;a[tt].dis=0;a[tt].cost=-cost;a[tt].nex=head[to];head[to]=tt;
}
bool vis[maxn];
int costs[maxn];
bool spfa(){
memset(vis,0,sizeof(vis));
memset(costs,0x3f,sizeof(costs));
queue<int> q;
vis[s]=1;
q.push(s);
costs[s]=0;
while(!q.empty()){
int top=q.front();
q.pop();
vis[top]=0;
for(int i=head[top];i;i=a[i].nex){
if(costs[top]+a[i].cost<costs[a[i].to]&&a[i].dis){
costs[a[i].to]=costs[top]+a[i].cost;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
if(costs[t]==costs[0]){
return 0;
}
return 1;
}
ll ans=0,anscost=0;
int dfs(int x,int minn){
if(x==t){
vis[t]=1;
ans+=minn;
return minn;
}
int use=0;
vis[x]=1;
for(int i=head[x];i;i=a[i].nex){
if((!vis[a[i].to]||a[i].to==t)&&costs[a[i].to]==costs[x]+a[i].cost&&a[i].dis){
int search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
anscost+=(a[i].cost*search);
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(spfa()){
do{
memset(vis,0,sizeof(vis));
dfs(s,inf);
}while(vis[t]);
}
printf("%lld",-1*anscost);
}
int main(){
scanf("%d%d%d%d",&numbe,&numde,&p,&q);
s=(p+1)*(q+1)+1;
t=s+1;
for(int i=1;i<=p+1;i++){
for(int j=1;j<=q;j++){
scanf("%d",&xx);
add((i-1)*(q+1)+j,(i-1)*(q+1)+j+1,1,-xx);//向右边的点连边
add((i-1)*(q+1)+j,(i-1)*(q+1)+j+1,inf,0);
}
}
for(int i=1;i<=q+1;i++){
for(int j=1;j<=p;j++){
scanf("%d",&xx);
add((j-1)*(q+1)+i,j*(q+1)+i,1,-xx);//向上面的点连边
add((j-1)*(q+1)+i,j*(q+1)+i,inf,0);
}
}
for(int i=1;i<=numbe;i++){
scanf("%d%d%d",&numro,&diry,&dirx);//源点向出生点连边
add(s,diry*(q+1)+dirx+1,numro,0);
}
for(int i=1;i<=numde;i++){
scanf("%d%d%d",&numro,&diry,&dirx);//撤离点向汇点连边
add(diry*(q+1)+dirx+1,t,numro,0);
}
dinic();
return 0;
}
P2763 \(\color{#9D3DCF}{试题库问题}\)
题目大意
有\(n\)道题和\(k\)种题目类型,每道题属于其中的若干类。现要出一张试卷,每类题目要若干道,题目不能重复出,给出一种可行的试题配置方案。
思路
建立超级源点和超级汇点,\(s\)连每一道题目,提供初始\(1\)的流量,因为每道题最多只能被选一次。每道题向其包含的类型连边,每个类型向\(t\)连边,权值为该类型需题数,跑最大流即可。
细节
无
代码
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 20005
#define maxm 50005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int n,k,s,t,sumxx,xx;
int task[maxn];
int head[maxn],tt=1;
struct node{
int to,dis,nex;
}a[maxm*2];
void add(int from,int to,int dis){
a[++tt].to=to;a[tt].dis=dis;a[tt].nex=head[from];head[from]=tt;
a[++tt].to=from;a[tt].dis=0;a[tt].nex=head[to];head[to]=tt;
}
bool vis[maxn];
int dep[maxn],cur[maxn];
bool bfs(){
for(int i=0;i<=t;i++){
vis[i]=0;
dep[i]=inf;
cur[i]=head[i];
}
queue<int> q;
vis[s]=1;
q.push(s);
dep[s]=0;
while(!q.empty()){
int top=q.front();
q.pop();
for(int i=head[top];i;i=a[i].nex){
if(dep[top]+1<dep[a[i].to]&&a[i].dis){
dep[a[i].to]=dep[top]+1;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
return dep[t]!=dep[0];
}
ll ans=0;
int dfs(int x,int minn){
if(x==t){
ans+=minn;
return minn;
}
int use=0;
for(int i=cur[x];i;i=a[i].nex){
cur[x]=i;
if(dep[a[i].to]==dep[x]+1&&a[i].dis){
int search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(bfs()){
dfs(s,inf);
}
}
void output(){
for(int i=1;i<=k;i++){
printf("%d:",i);
for(int j=head[i+n];j;j=a[j].nex){
if(a[j].dis==1){
printf(" %d",a[j].to);
}
}
printf("\n");
}
}
int main(){
scanf("%d%d",&k,&n);
s=n+k+1;
t=s+1;
for(int i=1;i<=n;i++){
add(s,i,1);
}
for(int i=1;i<=k;i++){
scanf("%d",&task[i]);
add(n+i,t,task[i]);
}
for(int i=1;i<=n;i++){
scanf("%d",&sumxx);
while(sumxx--){
scanf("%d",&xx);
add(i,xx+n,1);
}
}
dinic();
output();
return 0;
}
P2766 \(\color{#9D3DCF}{最长不下降子序列问题}\)
题目大意
给一个长度为\(n\)的数组\(a\),分行输出以下问题的答案:
\((1)\)最长不下降子序列长度\(s\);
\((2)\)长度为\(s\)的最长不下降子序列的个数(每个元素仅能出现一次);
\((3)\)长度为\(s\)的最长不下降子序列的个数(\(a_1\)与\(a_n\)能出现\(\infty\)次,其它只能出现一次)。
思路
- 第\((1)\)问
用\(DP\)解决即可,\(f_i\)表示前\(i\)个元素的答案,则\(f_i=\max\limits_{j=1 \&\& a_j \le a_i}^{i-1}{f_j} + 1\),最终答案就是\(\max\limits_{i=1}^{n}f_i\),记为\(s\)。 - 第\((2)\)问
用网络流解决。
建立超级源点和超级汇点\(s\)和\(t\),因为每一个点只能经过(被选取)\(1\)次,故将每个点\(i\)拆成两个点,编号为\(2\times i-1\)(入点)和\(2\times i\)(出点),连一条边权为\(1\)的边,故保证只能被选\(1\)次。之后,对于每一个点\(i\)来说,若\(f_i=1\),则将\(s\)与其之间连一条边权为\(1\)的边,因为可能可以从这个点开始找到符合要求的子序列;若\(f_i=s\),则将其与汇点连一条边权为\(1\)的边,因为其可能作为符合要求的子序列的终点。对于剩下的点,则与值比他大且\(f\)数组的值刚好大\(1\)的点相连(即点\(i\)要与所有\(a_j\ge a_i\)且\(f_j=f_i+1\)的点\(j\)项相连),最后跑最大流即可。 - 第\((3)\)问
同样的,但是此时不用重新建图,将\(s\)和\(1\)、\(n\)和\(t\)之间新建边权为\(\infty\)的边即可,因为上一问求得的答案仍要算进去,故不重新建图,直接在上一次跑完的图中跑看有没有剩下的。
细节
- 本题中是不下降子序列而不是单调递增的子序列。(\(\color{rgb(231,76,60)}{WA}\ \ On\ \ Test5\))
- \(n=1\)的情况特判。(\(\color{rgb(231,76,60)}{WA}\ \ On\ \ Test8\))
代码
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 20005
#define maxm 50005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int n,s,t,num[maxn],f[maxn];
int head[maxn],tt=1;
struct node{
int to,dis,nex;
}a[maxm*2];
void add(int from,int to,int dis){
a[++tt].to=to;a[tt].dis=dis;a[tt].nex=head[from];head[from]=tt;
a[++tt].to=from;a[tt].dis=0;a[tt].nex=head[to];head[to]=tt;
}
bool vis[maxn];
int dep[maxn],cur[maxn];
bool bfs(){
for(int i=0;i<=t;i++){
vis[i]=0;
dep[i]=inf;
cur[i]=head[i];
}
queue<int> q;
vis[s]=1;
q.push(s);
dep[s]=0;
while(!q.empty()){
int top=q.front();
q.pop();
for(int i=head[top];i;i=a[i].nex){
if(dep[top]+1<dep[a[i].to]&&a[i].dis){
dep[a[i].to]=dep[top]+1;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
return dep[t]!=dep[0];
}
int ans=0;
int dfs(int x,int minn){
if(x==t){
ans+=minn;
return minn;
}
int use=0;
for(int i=cur[x];i;i=a[i].nex){
cur[x]=i;
if(dep[a[i].to]==dep[x]+1&&a[i].dis){
int search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(bfs()){
dfs(s,inf);
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&num[i]);
}
//第(1)问
int ss=0;
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;j<i;j++){
if(num[i]>=num[j]){
f[i]=max(f[i],f[j]+1);
}
}
ss=max(ss,f[i]);
}
printf("%d\n",ss);
//第(2)问
s=n*2+1;
t=s+1;
for(int i=1;i<=n;i++){
add(2*i-1,2*i,1);
if(f[i]==1){
add(s,2*i-1,1);
}
if(f[i]==ss){
add(2*i,t,1);
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<i;j++){
if(num[j]<=num[i]&&f[j]+1==f[i]){
add(j*2,i*2-1,1);
}
}
}
dinic();
printf("%d\n",ans);
//第(3)问
if(n==1){
printf("1");
return 0;
}
add(s,1,inf);
add(1,2,inf);
if(f[n]==ss){
add(2*n-1,2*n,inf);
add(2*n,t,inf);
}
dinic();
printf("%d",ans);
return 0;
}
/*
4
4 3 2 1
1
1
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号