网络流24题 - 1

~~题目顺序按照洛谷“$\color{#13C2C2}{网络流24题}$”标签按难度排序。~~
~~题目的字体颜色为洛谷此题难度的颜色。~~
~~本人的题单：~~ 网络流24题

P4011 $\color{#3498DB}{孤岛营救问题}$

题目大意

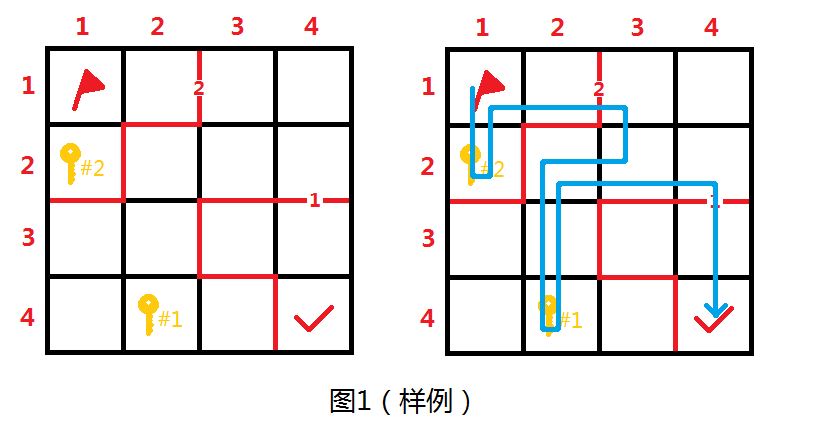
有一$n\times m$的迷宫，要从左上角$(1,1)$走到右下角$(n,m)$。迷宫内有墙（如下图纯红色部分）、门（下图有数字的红色部分，数字为钥匙编号）和钥匙（下图橙黄色部分，旁边数字为钥匙编号）。通过门必须有对应编号的钥匙，如下图要从$(1,2)$到$(1,3)$，一定要先去$(2,1)$拿$2$号钥匙。求到终点的最小步数（下图为$14$，路线为右图蓝色部分）。

思路

显然迷宫类的题第一时间就会想到$BFS$。~~不知道这题和下面的$P2761$等题为什么在网络流$24$题中。~~
我们从$(1,1)$开始爆搜，搜过一个点$(i,j)$就把$vis_{i,j}$更新为$1$，下次就不会来搜了。
但是，以图$1$为例，如果我们从$(1,1)$开始按上述方法搜，就会出现问题：先把$vis_{1,1}$设为$1$，假设从$(1,1)$先搜到$(1,2)$，$(1,2)$入队，队列中有$(1,2)$；$(1,1)$再搜到$(2,1)$，$(2,1)$入队，此处钥匙编号更新为$2$，队列中有$(1,2),(2,1)$（$(2,1)$有钥匙$2$），$(1,1)$搜完。把队首$vis_{1,2}$设为$1$，从$(1,2)$开始搜，搜$(1,3)$，但是没有钥匙过不去（此时$(1,2)$是没有钥匙的），搜完。把队首$vis_{2,1}$设为$1$，从$(2,1)$开始搜，搜到$(1,1)$，但是$vis_{1,1}=1$，搜过了，不搜，搜索结束。此时队列为空，输出$-1$表示无解。
但是，这种情况显然是有解的，为什么不能搜到呢？注意到搜到$(2,1)$拿到钥匙后由于$vis_{1,1}=1$，表示$(1,1)$被搜过，所以没有往下搜。换句话说，为什么这里可以从$(2,1)$向已经“搜过”的$(1,1)$继续搜呢？显然是因为我们在$(2,1)$拿到了钥匙，状态改变了，所以可以继续往下搜。所以，我们的$vis$数组要新开一维，记录有哪些钥匙（因为这题的$n,m,p\le 10$，所以开三维不会炸），当且仅当这个点搜过，且被搜的时候身上的钥匙和现在一样多才没有必要继续搜，即因为我们若身上多了钥匙，原来走过的地方可以再走一次，因为可能有原来开不开的门现在开得开了。
至于钥匙的存储就可以用状压了，用$2^i$即$1<<i$表示我们有了第$i$把钥匙，把所有的数按位或起来就表示我们有了哪些钥匙，到门的时候只要判
断$keys$&$(1<<door)$（$keys$为存钥匙的数，$door$表示需要的钥匙）是否为$1$就能判断能不能把门打开了。

细节

把$1$左移$i$位即为$2^i$，代码里为$1<<i$而不是$i<<1$。（$\color{rgb(231,76,60)}{WA}\ \ On\ \ Test3$）
一把编号为$i$的钥匙可以开多扇编号为$i$的门。~~这个一般不会犯错，因为没人想给自己增加码量。~~
一格里可能会有多把钥匙。~~这个很多人注意不到。~~（$\color{rgb(231,76,60)}{WA}\ \ On\ \ Test4$）

代码

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 55
using namespace std;
int n,m,p,k,bx1,by1,bx2,by2,g;
int key[maxn][maxn],barrier[maxn][maxn][maxn][maxn];
//key记录钥匙，key[i][j]记录(i,j)有哪些钥匙  barrier记录墙&门，墙记为p+1，门记为其编号
bool vis[maxn][maxn][1<<15];
struct node{
	int x,y;
	int keys;//存储有哪些钥匙
	int step;//步数
};
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};
bool flag=0;//记录是否有解
void bfs(){
	queue<node> q;
	node top,np;//top为队首,np为top可以到的上下左右四个点
	top.x=1;
	top.y=1;//开始把(1,1)入队
	top.keys=0;//没有钥匙
	top.step=0;//步数为0
	q.push(top);
	while(!q.empty()){
		top=q.front();
		q.pop();
		if(top.x==n&&top.y==m){//最先到(n,m)时的步数一定最小
			printf("%d",top.step);//输出并返回
			flag=1;
			return;
		}
		for(int i=0;i<4;i++){
			np.x=top.x+dx[i];
			np.y=top.y+dy[i];
			np.keys=top.keys;
			np.step=top.step+1;
			if(np.x<=0||np.x>n||np.y<=0||np.y>m){//出图 
				continue;
			}else if(barrier[top.x][top.y][np.x][np.y]==p+1){//有墙 
				continue;
			}else if(barrier[top.x][top.y][np.x][np.y]!=0){//有门 
				if((1<<barrier[top.x][top.y][np.x][np.y])&np.keys){//有钥匙,即可以过去 
					if(key[np.x][np.y]){//当前格有钥匙 
						np.keys|=key[np.x][np.y];
					}
					if(!vis[np.x][np.y][np.keys]){
						vis[np.x][np.y][np.keys]=1;
						q.push(np);
					} 
				}else{
					continue;
				} 
			}else{
				if(key[np.x][np.y]){//当前格有钥匙 
					np.keys|=key[np.x][np.y];
				}
				if(!vis[np.x][np.y][np.keys]){
					vis[np.x][np.y][np.keys]=1;
					q.push(np);
				} 
			}
		}
	}
}
int main(){
	scanf("%d%d%d",&n,&m,&p);
	scanf("%d",&k);
	for(int i=1;i<=k;i++){
		scanf("%d%d%d%d%d",&bx1,&by1,&bx2,&by2,&g);
		if(g==0){
			barrier[bx1][by1][bx2][by2]=p+1;//有墙则设为p+1
			barrier[bx2][by2][bx1][by1]=p+1;
		}else{
			barrier[bx1][by1][bx2][by2]=g;
			barrier[bx2][by2][bx1][by1]=g;
		}
	}
	scanf("%d",&k);
	for(int i=1;i<=k;i++){
		scanf("%d%d%d",&bx1,&by1,&g);
		key[bx1][by1]|=(1<<g);//把钥匙或起来,不能直接更新,因为一个点可能有多把钥匙
	}
	bfs();
	if(!flag){
		printf("-1");//无解输出-1
	}
	return 0;
}

P2756 $\color{#3498DB}{飞行员配对方案问题}$

题目大意

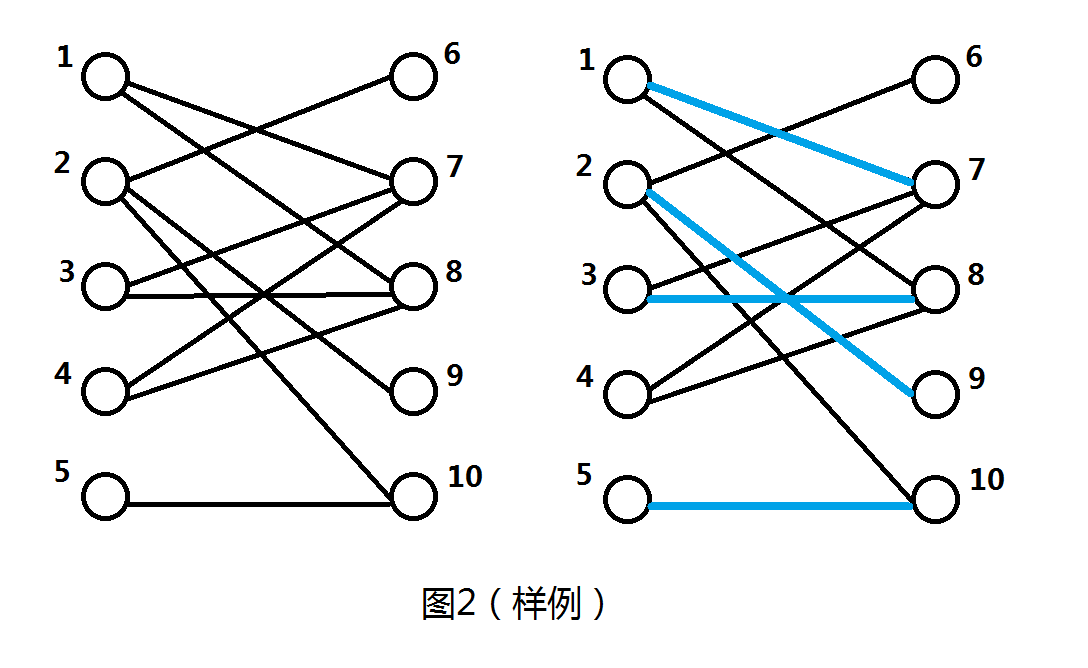
有两个点集，分别有$m$和$n-m$个点，两个点集的点互相之间有边，同一个点集内部的点没有边。现在要选出若干对点，每个点只能被选$1$次且每对点之间有边。求最大对数（图$2$右边的蓝色部分为最大方案之一）。

思路

其实就是二分图最大匹配。直接用匈牙利或者最大流跑即可。

细节

要输出其中一种方案。~~虽然看过题应该都不会错。~~
输入时依次输入$m$和$n$，是左边点集的点数和总点数，不是左右两边的点数。（$\color{rgb(231,76,60)}{WA}\ \ On\ \ Test4$）

代码

匈牙利

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 100
using namespace std;
int n,m,u,v;
int g[maxn][maxn];
int book[maxn],match[maxn];
int ans;
bool hungary(int x){
	for(int i=(n-m+1);i<=n;i++){
		if(g[x][i]&&!book[i]){
			book[i]=1;
			if(!match[i]||hungary(match[i])){
				match[i]=x;
				return 1;
			}
		}
	}
	return 0;
}
int main(){
	scanf("%d%d",&m,&n);
	for(int i=1;;i++){
		scanf("%d%d",&u,&v);
		if(u==-1&&v==-1){
			break;
		}
		g[u][v]=g[v][u]=1;
	}
	for(int i=1;i<=m;i++){
		memset(book,0,sizeof(book));
		if(hungary(i)){
			ans++;
		}
	}
	printf("%d\n",ans);
	for(int i=(n-m+1);i<=n;i++){
		if(match[i]){
			printf("%d %d\n",match[i],i);
		}
	}
	return 0;
}

最大流

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 5500
#define inf 1e8
using namespace std;
int n,m,e,s,t,u,v;
int head[maxn],tt=1;
struct node{
	int to,dis,nex;
}a[maxn];
void add(int from,int to,int dis){
	a[++tt].to=to;
	a[tt].dis=dis;
	a[tt].nex=head[from];
	head[from]=tt;
}
bool vis[maxn];
int dep[maxn],cur[maxn];
bool bfs(){
	for(int i=0;i<=t;i++){
		vis[i]=0;
		dep[i]=inf;
		cur[i]=head[i];
	}
	queue<int> q;
	vis[s]=1;
	q.push(s);
	dep[s]=0;
	while(!q.empty()){
		int top=q.front();
		q.pop();
		for(int i=head[top];i;i=a[i].nex){
			if(dep[top]+1<dep[a[i].to]&&a[i].dis){
				dep[a[i].to]=dep[top]+1;
				if(!vis[a[i].to]){
					vis[a[i].to]=1;
					q.push(a[i].to);
				}
			}
		}
	}
	if(dep[t]==dep[0]){
		return 0;
	}
	return 1;
}
int ans=0;
int dfs(int x,int minn){
	if(x==t){
		ans+=minn;
		return minn;
	}
	int use=0;
	for(int i=cur[x];i;i=a[i].nex){
		cur[x]=i;
		if(dep[a[i].to]==dep[x]+1&&a[i].dis){
			int search=dfs(a[i].to,min(minn-use,a[i].dis));
			if(search>0){
				use+=search;
				a[i].dis-=search;
				a[i^1].dis+=search;
				if(use==minn){
					break;
				}
			}
		}
	}
	return use;
}
void dinic(){
	while(bfs()){
		dfs(s,inf);
	}
	printf("%d\n",ans);
	for(int i=2;i<=tt;i+=2){
		if(a[i].to==t||a[i^1].to==t||a[i].to==s||a[i^1].to==s){
			continue;
		}
		if(!a[i].dis){
			printf("%d %d\n",a[i].to,a[i^1].to);
		}
	}
}
int main(){
	scanf("%d%d",&m,&n);
	for(int i=1;;i++){
		scanf("%d%d",&u,&v);
		if(u==-1&&v==-1){
			break;
		}
		add(u,v,1);
		add(v,u,0);
	}
	s=n+1;
	t=n+2;
	for(int i=1;i<=m;i++){
		add(s,i,1);
		add(i,s,0);
	}
	for(int i=m+1;i<=n;i++){
		add(i,t,1);
		add(t,i,0);
	}
	dinic();
	return 0;
}

P2761 $\color{#3498DB}{软件补丁问题}$

题目大意

某软件有$n$种$bug$（~~明明是特性~~），现有$m$种补丁，第$i$种补丁必须在有$B1_i$种$bug$且没有$B2_i$种$bug$时才能运行，效果是去除$F1_i$种$bug$但会新增$F2_i$种$bug$（$B,F$均为集合，即条件中均为多种$bug$），且会消耗$T_i$的时间。求去除所有$bug$所需的最短时间，无解输出$0$。

思路

~~这是一道最短路+状压的题。~~

最短路？
因为求时间最小值，我们可以把现在有哪些$bug$看作节点，把某补丁所需时间看做连接使用该补丁前后的两点之间的边的边权，这样，从起点（$n$种$bug$）到终点（没有$bug$）的最短路的边权和即为最短时间。
状压？
因为最多$20$种$bug$，我们考虑用状压存储$bug(s)$，即有第$i$种$bug$就把状态或上$1<<(i-1)$，如某时刻的状态为$(38)_{10}=(100110)_2$，表示此时有第$2,3,6$种$bug$。

现在考虑状态的变化。开始时，有全部$n$种$bug$，即状态为$\begin{matrix}（\underbrace{11\cdots1}）_2\\n个1\end{matrix}=(2^n-1)_{10}$，到结束时，没有一种$bug$，即状态为$0$。
对于每个补丁$i$，我们令$$cond1_i=\or_{j=1\And \And B1_{i_j}}{(1<<(B1_{i_j}-1))},cond2_i=\or_{j=1\And \And B2_{i_j}}{(1<<(B2_{i_j}-1))}$$ $$resu1_i=\or_{j=1\And \And F1_{i_j}}{(1<<(F1_{i_j}-1))},resu2_i=\or_{j=1\And \And F2_{i_j}}{(1<<(F2_{i_j}-1))}$$
其实就是把$B1_i,B2_i,F1_i,F2_i$四个数组的数（按上面高亮部分的方法）全部状压成一个数存进$cond1_i,cond2_i,resu1_i,resu2_i$中。比如第$i$个补丁需要有第$1,3,4$种错误而不能有第$2,5$种错误，那么$cond1_i=(1101)_2=(13)_{10},cond2_i=(10010)_2=(18)_{10}$。
那么如何判断某状态$x$下一个补丁能否使用、以及使用后的状态是什么呢？若一个补丁$i$能使用，则$cond1_i$的每一个是$1$的位$x$也为$1$，$cond2_i$的每一个是$1$的位$x$均不为$1$，因此应该满足$(x\and cond1_i)==cond1_i\And\And (x\and cond2_i)==0$。使用该补丁过后，$resu1_i$的每一个是$1$的位$x$均不为$1$，$resu2_i$的每一个是$1$的位$x$均为$1$，即使用补丁后的状态$y=(x\or resu1_1\or resu2_i)\oplus resu1_i$。
剩下的$SPFA$板子即可。

细节

这题的读入需要特别注意。
数组要开够。

代码

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 1<<21
using namespace std;
int n,m;
char x;
int t[maxn],cond1[maxn],cond2[maxn],resu1[maxn],resu2[maxn];
int ti[maxn],vis[maxn];
void spfa(){
	memset(ti,0x7f,sizeof(ti));
	queue<int> q;
	ti[(1<<n)-1]=0;
	q.push((1<<n)-1);//初始状态入队
	while(!q.empty()){
		int top=q.front();
                vis[top]=0;//队头出队
		q.pop();
		for(int i=1;i<=m;i++){
			if(((top&cond1[i])==cond1[i])&&((top&cond2[i])==0)){//能使用补丁i 
				int news=(((top|resu1[i])^resu1[i])|resu2[i]);//使用后状态 
				if(ti[top]+t[i]<ti[news]){//时间更短则更新
					ti[news]=ti[top]+t[i];
					if(!vis[news]){//不在队中则入队
						vis[news]=1;
						q.push(news);
					}
				}
			}
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d",&t[i]);
		scanf("%1c",&x);//筛掉空格 
		for(int j=1;j<=n;j++){
			scanf("%1c",&x);
			if(x=='+'){//要有的bug 
				cond1[i]|=(1<<(j-1));
			}else if(x=='-'){//不能有的bug 
				cond2[i]|=(1<<(j-1));
			}
		}
		scanf("%1c",&x);
		for(int j=1;j<=n;j++){
			scanf("%1c",&x);
			if(x=='-'){//能修复的bug 
				resu1[i]|=(1<<(j-1)); 
			}else if(x=='+'){//要新增的bug 
				resu2[i]|=(1<<(j-1));
			}
		}
	}
	spfa();
	if(ti[0]==2139062143){//无法到0则无解
		printf("0");
	}else{
		printf("%d",ti[0]);
	}
	return 0;
}
/*
3 3
1 000 00-
1 00- 0-+
2 0-- -++
*/

P4016 $\color{#3498DB}{负载平衡问题}$

题目大意

一个环上有$n$个仓库，仓库$i$初始有$a_i$个单位的货物。相邻两个仓库可以互相输送货物，输送$1$个单位的货物的代价是$1$，求让每个仓库货物相同的最小代价。

思路

本题有两种做法。

数学

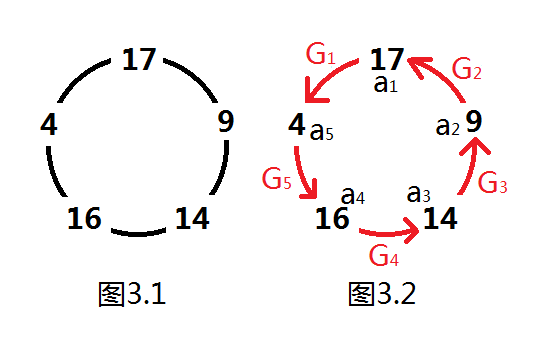
设第$i$个仓库一开始有$a_i$的货物，给逆时针方向下一个仓库$G_i$的货物。
运完之后，各仓库的容量一样，显然为$\overline{x}$，所以有以下式子：
$\begin{cases}a_1-G_1+G_2=\overline{x}\\a_2-G_2+G_3=\overline{x}\\a_3-G_3+G_4=\overline{x}\\…\\a_i-G_i+G_{i+1}=\overline{x}\end{cases}$
以$G_2$为例，变形一下，得到$G_2=\overline{x}+G_1-a_1$，则有以下式子：
$\begin{cases}G_1=G_1\\G_2=\overline{x}+G_1-a_1\\G_3=\overline{x}+G_2-a_2\\…\\G_i=\overline{x}+G_{i-1}-a_{i-1}\end{cases}$
以$G_2$为例，换元，得到$G_2=\overline{x}+G_1-a_1$；以$G_3$为例，换元，得到$G_3=2\overline{x}+G_1-(a_1+a_2)$，则有以下式子：
$\begin{cases}G_1=G_1\\G_2=\overline{x}+G_1-a_1\\G_3=2\overline{x}+G_1-(a_1+a_2)\\…\\G_i=i·\overline{x}+G_1-(\sum\limits_{j=1}^{i-1}{a_j})\end{cases}$
令$F_i=\sum\limits_{j=1}^{i-1}{a_j}-(i-1)·\overline{x}$，则上述式子变成：
$\begin{cases}G_1=G_1-F_1\\G_2=G_1-F_2\\G_3=G_1-F_3\\…\\G_i=G_1-F_i\end{cases}$
又因为答案$ans=\sum\limits_{i=1}^{n}{|G_i|}$，所以展开，$ans=|G_1-F_1|+|G_1-F_2|+|G_1-F_3|+…+|G_1-F_n|$
这个式子是不是很熟悉？它的几何意义是数轴上一点$G_1$到$n$个点$F_1,F_2,…,F_n$的距离的和。显然不管$n$取多少时，当$G_1$取它们的中位数$\overline{F}$时式子总取最大。所以计算出$F_1\sim F_n$排序，取中位数，模拟即可。
那么，如何算出$F_i$呢？我们注意到，$F_{i-1}=\sum\limits_{j=1}^{i-2}{a_j}-(i-1)·\overline{x},F_i=\sum\limits_{j=1}^{i-1}{a_j}-i·\overline{x}$，两式相减得到$F_i=F_{i-1}-\overline{x}+a_{i-1}$。
最小费用最大流

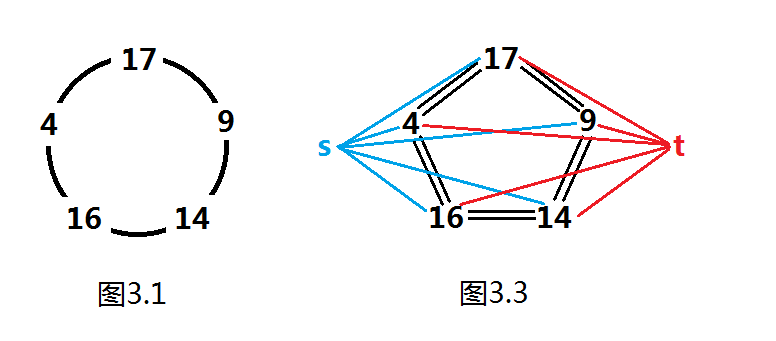
考虑到本题在网络流$24$题中，还是决定写一下网络流做法。
首先是建点，建立超级源点和超级汇点。
然后是建边，超级源点和超级汇点肯定要连接所有点，而且因为相邻两点间可以互相运送，所以相邻的两点间也要建立两条边。
之后是边权，以源点为起点的边的边权为$a_i$，$i$为边的终点，因为要把起始的水给点；以汇点为终点的边的边权为$\overline{x}$，因为最后每个点的水量都应是$\overline{x}$；两点间的边容量为$+\infty$，因为无论多少水都应该可以流。
再就是费用，源点与汇点的边的边权为$0$，因为水往这里流不计任何代价。相邻两仓库间边权为$1$，运送$1$单位的货物要有$1$的代价。
最后是答案，用$EK/Dinic$跑最小费用最大流得到的就是最后答案。

细节

没啥细节，板子别错

代码

数学

点击查看代码

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define maxn 105
using namespace std;
int n;
int a[maxn],tot;
int f[maxn];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		tot+=a[i];
	}
	f[1]=a[1]-(tot/n);
	for(int i=2;i<=n;i++){
		f[i]=f[i-1]+a[i-1]-(tot/n);
	}
	sort(f+1,f+1+n);
	int minn=(n%2?f[(n+1)/2]:(f[n/2]+f[(n+1)/2])/2),ans=0;
	for(int i=1;i<=n;i++){
		ans+=abs(minn-f[i]);
	}
	printf("%d",ans);
	return 0;
}

最小费用最大流

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 5005
#define maxm 50005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int n,s,t,num[maxn],tot;
int head[maxn],tt=1;
struct node{
	int to,dis,cost,nex;
}a[maxm*2];
void add(int from,int to,int dis,int cost){
	a[++tt].to=to;
	a[tt].dis=dis;
	a[tt].cost=cost;
	a[tt].nex=head[from];
	head[from]=tt;
}
bool vis[maxn];
int costs[maxn];
bool spfa(){
	memset(vis,0,sizeof(vis));
	memset(costs,0x3f,sizeof(costs));
	queue<int> q;
	vis[s]=1;
	q.push(s);
	costs[s]=0;
	while(!q.empty()){
		int top=q.front();
		q.pop();
		vis[top]=0;
		for(int i=head[top];i;i=a[i].nex){
			if(costs[top]+a[i].cost<costs[a[i].to]&&a[i].dis){
				costs[a[i].to]=costs[top]+a[i].cost;
				if(!vis[a[i].to]){
					vis[a[i].to]=1;
					q.push(a[i].to);
				}
			}
		}
	}
	if(costs[t]==costs[0]){
		return 0;
	}
	return 1;
}
ll ans=0,anscost=0;
int dfs(int x,int minn){
	if(x==t){
		vis[t]=1;
		ans+=minn;
		return minn;
	}
	int use=0;
	vis[x]=1;
	for(int i=head[x];i;i=a[i].nex){
		if((!vis[a[i].to]||a[i].to==t)&&costs[a[i].to]==costs[x]+a[i].cost&&a[i].dis){
			int search=dfs(a[i].to,min(minn-use,a[i].dis));
			if(search>0){
				use+=search;
				anscost+=(a[i].cost*search);
				a[i].dis-=search;
				a[i^1].dis+=search;
				if(use==minn){
					break;
				}
			}
		}
	}
	return use;
}
void dinic(){
	while(spfa()){
		vis[t]=1;
		while(vis[t]){
			memset(vis,0,sizeof(vis));
			dfs(s,inf);
		}
	}
	printf("%lld",anscost);
}
int main(){
	scanf("%d",&n);
	s=n+1;//超级源点 
	t=n+2;//超级汇点 
	for(int i=1;i<=n;i++){
		scanf("%d",&num[i]);
		tot+=num[i];
	}
	for(int i=1;i<n;i++){//建边(不要忘了反向边)
		add(i,i+1,inf,1);//与下一个点
		add(i+1,i,0,-1);
		add(i+1,i,inf,1);//下一点与它
		add(i,i+1,0,-1);
		add(s,i,num[i],0);//与源点相连
		add(i,s,0,0);
		add(i,t,tot/n,0);//与汇点相连
		add(t,i,0,0);
	}
	add(n,1,inf,1);
	add(1,n,0,-1);
	add(1,n,inf,1);
	add(n,1,0,-1);
	add(s,n,num[n],0);
	add(n,s,0,0);
	add(n,t,tot/n,0);
	add(t,n,0,0);
	dinic();//Dinic板子
	return 0;
}

$To\ be\ continued…$

posted @ 2021-08-23 11:06 qzhwlzy 阅读(83) 评论(0) 收藏举报

刷新页面返回顶部

preparing

qzhwlzy

网络流24题 - 1

P4011 \(\color{#3498DB}{孤岛营救问题}\)

题目大意

思路

细节

代码

P2756 \(\color{#3498DB}{飞行员配对方案问题}\)

题目大意

思路

细节

代码

P2761 \(\color{#3498DB}{软件补丁问题}\)

题目大意

思路

细节

代码

P4016 \(\color{#3498DB}{负载平衡问题}\)

题目大意

思路

细节

代码

公告