手撕深度学习之CUDA矩阵乘法（下篇）：从Block Tiling到Warp Tiling，四步优化实现性能近90%的飞跃

本文首发于本人微信公众号，文章链接：https://mp.weixin.qq.com/s/ThIoGBxvF-L0eH-Z8Kk5vQ

摘要

本文是CUDA矩阵乘法系列文章的下篇，主要介绍了4种CUDA矩阵乘法内核的实现及其优化来源，并以一个内核为例详细展示了编写复杂矩阵乘法内核的方法和技巧。

最终本文展示了一种达到 cuBlas性能87% 的实现。

前言

本文是CUDA矩阵乘法系列文章的下篇。前两篇文章分别介绍3种简单的CUDA矩阵乘法Kernel实现，以及Nsight Compute这一强大工具的使用。

本文将接着上篇，继续介绍4种更为高效的Kernel实现，以及其优化的来源。

V4: 1D Block Tiling

在V3里面，我们Cache-Blocking的方式减少了GMEM的访问次数，从而提升了性能。

注意到，在V3里面每个线程只负责计算C里的一个元素，但是对于C中的每一列，它们要用到的B中的数据都是相同的，如下图所示：

T1和T2会访问B中的同一列

这一类“非必要”的内存访问正是我们的实现和理论性能差距这么大的元凶：

因为在最理想的情况下，只需要读取一次B矩阵就能够得到完成矩阵乘法所需要的全部信息，但是实际实现时我们却重复读取了多次。

那么应该如何避免这一问题呢？这就要用到之前我们在介绍并行规约算法的文章中提到的算法级联的技巧了。

也就是让一个线程计算多个C的值，来尽量复用每个线程读到寄存器里的信息，最终减少整体的内存访问数量。

在V4里面，我们先尝试在行这个维度进行扩展，即让一个线程计算C中的某一列的多个元素，如下图所示（这里用不用的背景色区分了每个线程需要负责计算的C的元素）：

实现细节

这一想法理解起来非常简单，但是实现起来是比较烧脑的。

即使是在理解了这个Kernel的基本思想的前提下，直接去看参考文章的作者的代码大概率也会被一堆不明所以的循环整的一脸懵逼。

所以我认为，记录一下写出实现代码的方法是很有必要的。接下来会是一个手把手的教程，教你如何无痛写出复杂的矩阵乘法Kernel实现。

（Tips：下面的内容会有些烧脑和抽象，建议在阅读的同时尝试自己动手实现一下，可以考虑使用本文配套的开源代码

https://github.com/QZero233/CudaMM

把其中namespace V4里面的部分删掉之后自己动手实现一下，这份源码里配备了正确性检查功能和性能测试功能，可以帮助大家确认自己实现的Kernel的正确性与质量）

首先把焦点集中到输出矩阵C上，我们需要明确每个线程需要计算的C的位置，还是如上图所示，这里我们有3个常量：

ROW_BLOCK_SIZE表示一个Block（线程块）负责计算的C的行数，COL_BLOCK_SIZE表示列数，TILE_ROW_SIZE表示每个线程在列方向上需要计算的C的元素数量。

接下来再把焦点放到每个线程上，我们可以由此计算出这个线程所在的Block负责的C的左上角的坐标：

outTopLeftX = blockIdx.x * ROW_BLOCK_SIZE
outTopLeftY = blockIdx.y * COL_BLOCK_SIZE

同时还可以计算出这个线程在Block内的坐标

threadX = threadIdx.x / COL_BLOCK_SIZE
threadY = threadIdx.x % COL_BLOCK_SIZE

这时候，我们就已经知道：

• 这个线程要计算TILE_ROW_SIZE个C
• 它们的列坐标（Y）都是outTopLeftY + threadY
• 它们的行坐标（X）处于 [outTopLeftX + threadX , outTopLeftX + threadX + TILE_ROW_SIZE) 这个区间

在有了上述信息后，我们就已经可以根据坐标读取A和B中对应的行和列从而进行计算了。

但是为了更好的性能表现，我们还需要结合V3里的优化技巧，把行和列的一部分加载到SMEM（共享内存）中。

在开始实现这一结合之前，还需要介绍一个小技巧：

后面会涉及到很多根据坐标读取数组元素的操作，坐标到下标的转换本身并不复杂，只需要使用公式 x * col_num + y 即可。

但是如果把坐标本身的计算也放在了下标计算中，那这个表达式就会变得很难理解，例如参考文章作者这里的的代码：

regM[wSubRowIdx * TM + i] =As[(dotIdx * BM) + warpRow * WM + wSubRowIdx * WSUBM + threadRowInWarp * TM + i];

我们可以用C++的lambda表达式做一个自己的语法糖，来让坐标到下标的转换更可读，如下所示：

__device__ inline uint32_t idx(uint32_t x, uint32_t y, uint32_t row_num, uint32_t col_num) {
        return x * col_num + y;
}

// 用lambda表达式计算二维坐标对应的下标
const auto aIdx = uint32_t x, uint32_t y {
    return idx(x, y, M, N);
};
const auto bIdx = uint32_t x, uint32_t y {
    return idx(x, y, N, P);
};

// 使用示例：访问A的(2,3)
float x = A[aIdx(2, 3)];

这里是不用担心性能问题的，这里的lambda表达式很轻，编译器会自动把这些表达式内联，不会编译成函数调用。

OK，继续回到我们的主线任务。先简单回顾一下V3里面我们是怎么做的：

如上图所示，我们以K_STEP为滑动窗口的大小，每次加载K_STEP列的A和K_STEP行的B，计算完成中间结果后把滑动窗口向后移动，直到完成计算。

所以具体到每个线程而言，需要在每个滑动窗口内按顺序完成这样两件事：

第一步，把对应的A和B中的元素加载到SMEM中；第二步，使用SMEM完成自己应负责的计算。

对于第一步，由于我们设置的ROW_BLOCK_SIZE=COL_BLOCK_SIZE=64, TILE_ROW_SIZE=8, K_STEP=8

所以每个Block内会有(ROW_BLOCK_SIZE * COL_BLOCK_SIZE) / TILE_ROW_SIZE = 512个线程

这恰好和As的元素个数 ROW_BLOCK_SIZE * K_STEP，以及Bs的元素个数 K_STEP * COL_BLOCK_SIZE 相同

所以每个线程只需要加载一个元素到As与Bs里即可完成任务。

那么接下来就很简单了，根据threadIdx计算当前线程需要把数据加载到As和Bs的哪个位置，然后再以outTopLeft的坐标为偏移量完成加载即可，代码如下所示：

// 加载As和Bs

// 这里As的大小为 ROW_BLOCK_SIZE * K_STEP，线程数量为 (ROW_BLOCK_SIZE / ROW_TILE_SIZE) * COL_BLOCK_SIZE
// 两者应该恰好相等，否则无法把As装载完成
// 如果相等，就能通过编排的方式完成装载
assert((ROW_BLOCK_SIZE * K_STEP) == ((ROW_BLOCK_SIZE / TILE_ROW_SIZE) * COL_BLOCK_SIZE)); //会常量展开的，不影响性能
// 这里计算每个线程负责装载到As的哪个位置
const uint32_t asLoadX = threadIdx.x / K_STEP;
const uint32_t asLoadY = threadIdx.x % K_STEP;
// 该线程负责搬运 A[outTopLeftX + asLoadX][k + asLoadY] -> As[asLoadX][asLoadY]
As[asIdx(asLoadX, asLoadY)] = a[aIdx(outTopLeftX + asLoadX, k + asLoadY)];

// Bs同理
assert((K_STEP * COL_BLOCK_SIZE) == ((ROW_BLOCK_SIZE / TILE_ROW_SIZE) * COL_BLOCK_SIZE));
const uint32_t bsLoadX = threadIdx.x / COL_BLOCK_SIZE;
const uint32_t bsLoadY = threadIdx.x % COL_BLOCK_SIZE;
// 这里搬运 B[k + bsLoadX][outTopLeftY + bsLoadY] -> Bs[bsLoadX][bsLoadY]
Bs[bsIdx(bsLoadX, bsLoadY)] = b[bIdx(k + bsLoadX, outTopLeftY + bsLoadY)];

对于第二步，一个最直接的方法就是循环TILE_ROW_SIZE次，每次计算一个元素，这种实现当然是可行的。

但是我们注意到，我们的计算实际只需要用到Bs中同一行的元素，如果每次计算都重新读取这一行，那就会造成“非必要”的内存访问，所以取而代之的，我们有下面这种只需要加载一次Bs的实现方法：

// 循环计算 tmp[tile] += As[threadX * TILE_ROW_SIZE + tile][:] * Bs[:][threadY] ，其中 tile: 0 -> ROW_TILE_SIZE
// 计算完成的 tmp[tile] 就是 OUT[x * TILE_ROW_SIZE + tile][threadY]
// 这一步可以缓存 Bs[:][threadY] 以复用
for (uint32_t i = 0; i < K_STEP; i++) {
    const scalar_t tmpB = Bs[bsIdx(i, threadY)];
    for (uint32_t tile = 0; tile < TILE_ROW_SIZE; tile++) {
        tmp[tile] += As[asIdx(threadX * TILE_ROW_SIZE + tile, i)] * tmpB;
    }
}

至此，Kernel的主体就已经完成了，最后只剩下了把中间结果写入到C里面。

由于之前已经计算出了每个线程负责的C的坐标，所以只需要按部就班地进行一个写回即可，代码如下所示：

// 写回结果
for (uint32_t tile = 0; tile < TILE_ROW_SIZE; tile++) {
    out[outIdx(outTopLeftX + threadX * TILE_ROW_SIZE + tile, outTopLeftY + threadY)] = tmp[tile];
}

（一个题外话：这里稍微改动一下就可以变成标准的GEMM了）

实验结果

如下图所示：

性能是V3版本的2倍多，目前已经达到cuBlas的34%了。

优化来源分析

V4为什么会比V3更快呢？

答案是SMEM的访问次数减少了，这里我们可以做一个计算来分析一下：

在一个K_STEP内，两者写SMEM的次数是相同的，但是读SMEM次数不同。

在V3里，每个线程会读2 * BLOCK_SIZE次，一共有1024个线程，所以读取次数为65536次；

而在V4里，每个线程读 K_STEP + K_STEP * TILE_ROW_SIZE次，一共有512个线程，所以总共的读取次数为36864次，几乎是V3的一半了，所以这里性能翻倍也是符合预期的。

Nsight Compute展示的数据也能佐证这一计算：
这是V3的：

而这是V4的：

而究其根本，这一优化是在向最理想的内存读取次数靠拢：即总共只完整读取一次矩阵A和B。

V5: 2D Block Tiling

在V5里面，我们更进一步，让一个线程负责的区域从一个一维的列变成一个二维的区域。如下图所示：

实现方式也和V4大同小异。在加载到SMEM那一步中，由于设定发生了变化，计算之后发现需要每个线程加载多个元素到SMEM中。

在计算结果的那一步中，参考文章作者提出了一种类似的技巧来复用As和Bs中的行与列，如下所示：

// 这里经过优化，把SMEM访问次数从 TILE_ROW_SIZE * TILE_COL_SIZE * K_STEP
// 变为了 K_STEP * (TILE_ROW_SIZE + TILE_COL_SIZE)
// 能这么做的本质原因在于，计算OUT中的元素时，是存在复用的，比如(0, 0)和(0, 1)会共用As的第0行
// 这里巧妙构造之后将这个复用实现了
// 但是我这边实测下来，下面这个实现比上面的要慢接近50%
for (uint32_t i = 0; i < K_STEP; i++) {
    for (uint32_t tile_row = 0; tile_row < TILE_ROW_SIZE; tile_row++) {
        a_reg[tile_row] = As[asIdx(threadX * TILE_ROW_SIZE + tile_row, i)];
    }

    for (uint32_t tile_col = 0; tile_col < TILE_COL_SIZE; tile_col++) {
        b_reg[tile_col] = Bs[bsIdx(i, threadY * TILE_COL_SIZE + tile_col)];
    }

    for (uint32_t tile_row = 0; tile_row < TILE_ROW_SIZE; tile_row++) {
        for (uint32_t tile_col = 0; tile_col < TILE_ROW_SIZE; tile_col++) {
            tmp[tile_row * TILE_COL_SIZE + tile_col] += a_reg[tile_row] * b_reg[tile_col];
        }
    }
}

实验结果

按照参考文章作者的思路实现后，结果如下，发现并没有带来多少优化。

但是很诡异的是，我尝试了另外一种实现，把基于regs的优化替换成了更直观的方式，如下所示：

// 计算OUT
for (uint32_t tile_row = 0; tile_row < TILE_ROW_SIZE; tile_row++) {
    for (uint32_t tile_col = 0; tile_col < TILE_COL_SIZE; tile_col++) {
        for (uint32_t i = 0; i < K_STEP; i++) {
            tmp[tile_row * TILE_COL_SIZE + tile_col] += As[asIdx(threadX * TILE_ROW_SIZE + tile_row, i)] * Bs[bsIdx(i, threadY * TILE_COL_SIZE + tile_col)];
        }
    }
}

诡异的是，此时性能直接翻倍了，如下所示：

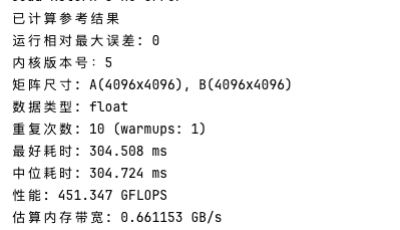
诡异现象成因

这一现象是Bank Conflict引起的

因为在当前的布局下，一个Warp里，threadX会有16种取值，而TILE_ROW_SIZE这个stride的取值是8

这就导致了在访问As时会发生Bank Conflict，这一点在上一篇文章中有详细分析过，这里就不再赘述了。

V6: Vectorize

在V6里面，我们会使用向量化这一内存访问模式来进一步优化内存访问。

向量化在基于CPU的计算加速中也是一个常用的技巧，其原理是：如果我们要访问的内存区域是连续的4个字节，那么就可以通过一条指令同时完成4个字节的访存（例如SASS里的LDS.128指令）。

在代码实现中，我们使用float4这个数据类型来表示4字节的向量化操作

下面这段代码展示了float4的基本用法：可以访问其每个分量，也可以直接一整个地进行赋值操作

float4 tmp =
    reinterpret_cast<float4 *>(&A[innerRowA * K + innerColA * 4])[0];
As[(innerColA * 4 + 0) * BM + innerRowA] = tmp.x;
As[(innerColA * 4 + 1) * BM + innerRowA] = tmp.y;
As[(innerColA * 4 + 2) * BM + innerRowA] = tmp.z;
As[(innerColA * 4 + 3) * BM + innerRowA] = tmp.w;

reinterpret_cast<float4 *>(&Bs[innerRowB * BN + innerColB * 4])[0] =
    reinterpret_cast<float4 *>(&B[innerRowB * N + innerColB * 4])[0];

需要注意的是，使用reinterpret_cast把地址转成float4时，需要保证地址是16字节对齐的。

这里的具体实现和V5也是大同小异，唯一的区别就是加载时使用量向量化技巧，所以每个线程处理的元素数量变成了4个，完整实现代码可以参考GitHub上的源码，这里不再赘述了。

实验结果

参考文章作者在这里同样使用了regs来做优化，但是同样的，这里测下来发现引入regs优化后会更慢。

这里同样也是Bank Conflict带来的问题，Nsight Compute可以验证这一点：

而且可以发现，参考文章作者的Kernel 6也有同样的问题

下面是没有使用regs版本的性能数据：

此时性能数据已经达到了cuBlas的71%

这个例子说明了，Kernel内存访问模式是一个需要权衡的东西，有时候减少了内存访问次数，但是带来了Bank Conflict，最终的性能还是会下降的。

V10: Warp Tiling

参考文章作者直接跳过了Kernel 7, Kernel 8，而Kernel 9是用了Auto-tuning，这里就直接跳过了，直接进入Kernel 10。

对于V10，参考文章作者并没有解释的很清楚，这使得我在看完之后疑惑了很久，不知道这一优化的来源是什么。

V10相较于V6的不同之处在于：V10改变了Block里Warp的排布方式，如下图所示：

图里每个方格代表一个线程，相同背景色的方格组成一个Warp

（注：每个线程实际会负责计算多个C的值，这里相当于是把这多个值“压缩”到了一格内）

假设V6一个Block里有128个线程，也就是4个Warp，那么每个Warp以及其内部的线程负责的区域就如上图所示。

而在V10中，这一分布被改为了如下图所示的分布：

但是这一变化是如何带来性能提升的呢？参考文章作者并没有指明这一点，AI也没能给出答案。

最后在Nsight Compute的帮助下，这个问题的答案得到了揭晓：这一优化的根本原因是：Bank Conflict数量减少了。

正如我们在中篇里提到的，在V10里面，threadY有8种取值，TILE_COL_SIZE为4，这就避免了在访问Bs时的Bank Conflict；

而在V6里面，threadY的取值有16种，且TILE_COL_SIZE为8，这就不可避免地会出现Bank Conflict。

V10的具体实现依然是有一定难度的，大体上也可以参考V4的实现来完成，这里就不对具体实现展开赘述了。

实验结果

此时已经达到了cuBlas的87%

总结

对于《How to Optimize a CUDA Matmul Kernel for cuBLAS-like Performance: a Worklog》的学习记录到这里也就结束了。

在这个过程中，我们学到了CUDA内存访问的优化方法，初识了Nsight Compute这一强大工具，同时也练习了复杂CUDA算子的实现，最终我们实现了一个性能达到cuBlas 87%的矩阵乘法Kernel。

但是实现一个能够在生产环境使用的GEMM算子并非易事，这需要在保证正确性的前提下，针对各种不同的形状进行针对性的优化，这是一个工程量极大同时也非常具有挑战性的工作。

在写这篇文章的前几天，NVIDIA刚发布了cuTile，使用这一新技术可以让我们以更低的复杂度调用Tensor Core来实现更高性能的矩阵乘法；与之类似的还有Triton DSL等基于Python的高性能算子框架。

现如今，使用Python做算子开发成为了一种新的潮流范式，相关的技术支持也在向这一方向靠拢，后续我也会往这个方向继续深挖。

最后再次感谢《How to Optimize a CUDA Matmul Kernel for cuBLAS-like Performance: a Worklog》作者SiBoehm大佬的知识开源，这篇文章的配图非常简明精美，推荐大家阅读学习。