作业5_矩阵的逆与线性方程组的通解

1. 用本文件后面的程序在求下列方程组的解的同时求出系数矩阵的逆矩阵和系数矩阵行列式。

（1）

 

 

 

参考解为：

x =(11.5,-1.5,-4.,0.,-2.)^T

（2）

 

 

 

参考解为：

 

 

 

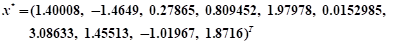
2. 试思考如何编写程序求下面方程组的解

 

 

 

 

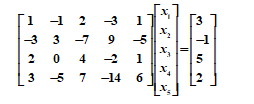
//========  gauss.txt中的数据 =========

 

 

/*

算例1

5

 1  -1   2  -3   1   3

-3   3  -7   9  -5  -1

 2   0   4  -2   1   5

 3  -5   7  -14  6   2

 4  -4   10 -10  2   8

*/

/* 算例2

 

10

 4  2  -3  -1   2   1   0  0  0  0   5

 8  6  -5  -3   6   5   0  1  0  0  12

 4  2  -2  -1   3   2  -1  0  3  1   3

 0 -2   1   5  -1   3  -1  1  9  4   2

-4  2   6  -1   6   7  -3  3  2  3   3

 8  6  -1   3   7  17   2  6 -3  5  46

 0  2  -1   3  -4   2   5  3  0  1  13

16 10 -11  -9  17  34   2 -1  2  2  38

 4  6   2  -7  13   9   2  0 12  4  19

 0  0  -1   8  -3  -24 -8  6  3 -1 -21

*/

 

 

//=======================================================

//==== 求解线性方程组同时求系数矩阵的行列式和逆矩阵解====

//=======================================================

#include<stdio.h>

#include<math.h>

void main()

{

       double a[15][15], x[15], temp, mt[15][15], c[15][15];

       double det = 1, b[15][15]={0};       // 增加两个变量, det :存放行列的值,

                                            // b[][]:存放逆矩阵,所有元素均设为0

       int i, j, k, n, flag;

       FILE *f;

       f = fopen ("d:\\gauss.txt", "r");   

       fscanf(f, "%d", &n);                 // 读入议程组的阶数

 

       puts("方程组的增广矩阵为：");

 

       for (i=1; i<=n; i++)                 // 读入议程组的增广矩阵的数据

       {

              for(j=1; j<=n+1; j++)

              {

                     fscanf(f, "%lf", &a[i][j]);

                     mt[i][j] = a[i][j];         // 备份

                     printf("%7.3lf", a[i][j]);  //  输出增广矩阵的值

              }

              puts("");

       }

       fclose(f);                      //   a[][] |  b[][]= E

                                       //   E     |  a^(-1)

       for(i=1; i<=n; i++)             

              b[i][i] = 1;   // b[][]初始时为单位矩阵,即对角线上的元素都设为1

                          // b[][]与a[][]做相同的行变换

 

       puts("");

 

       for (k=1; k<=n; k++)

       {

                        //找主无素

              flag = k;

              temp = fabs(a[k][k]);

              for(i=k+1; i<=n; i++)

              {

                     if(fabs(a[i][k]) > temp)

                     {

                            temp = fabs(a[i][k]);

                            flag = i;

                     }

              }

 

              if (flag != k)         // 找到的主元素如果不是a[k][k]， 交换行

              {

                     det = det * (-1);  // 换一次行，行列式的值改变一次符号

                     for (j=1; j<=n+1; j++) // 交换第k行和第flag行

                     {

                            temp=a[k][j];         // 对a[][]进行变换，消元

                            a[k][j] = a[flag][j];

                            a[flag][j] = temp;

                                      // 矩阵 b[][] 做相同的行变换

                            temp=b[k][j];

                            b[k][j] = b[flag][j];

                            b[flag][j] = temp;

                     }

              }

              //消元

              temp = a[k][k];

              det = det * temp;  // 化为三角阵后，对角线上元素的乘积为行列式的值

                                 // 主元素的积即为行列式的值

              for (j=1;j<=n+1; j++ )   // 第k行除以主元素

              {

                     a[k][j] /= temp;  

                     b[k][j] /= temp;     // 矩阵 b[][] 做相同的行变换                 

 

              }

 

              for(i=k+1; i<=n; i++)

              {

                     temp = a[i][k];

                     for(j=1; j<=n+1; j++)

                     {

                            a[i][j] = a[i][j] - temp * a[k][j];

                                                  // 矩阵 b[][] 做相同的行变换   

                            b[i][j] = b[i][j] - temp * b[k][j];

                     }

              }

       }                          //  回代即可得方程组的解

                                  //  行列式已得

       puts("方程组的增广矩阵化为上三角阵：");

 

       for (i=1; i<=n; i++)            // 输出增广矩阵的最终形式,

       {

              for(j=1; j<=n+1; j++)

                     printf("%7.3lf", a[i][j]);

              puts("");

       }

 

 

  

    puts("");

       for (k=n; k>=1; k--)    // 在上三角矩阵的基础上将系数矩阵化为单位矩阵

       {

              for (i=k-1; i>=1; i--)

              {

                     temp = a[i][k];

                     for (j=1; j<=n+1; j++)

                     {

                            a[i][j] = a[i][j] - a[k][j] * temp;

                            b[i][j] = b[i][j] - b[k][j] * temp;  // 矩阵 b[][] 做相同的行变换                         

                     }

              }

       }

 

       puts("方程组的增广矩阵最终变为：");

 

       for (i=1; i<=n; i++)            // 输出增广矩阵的最终形式,

       {

              for(j=1; j<=n+1; j++)

                     printf("%7.3lf", a[i][j]);

              puts("");

       }

 

       puts("上面矩阵最后一列即为方程组的解：");

 

 

       puts("");

 

       printf("系数矩阵的行列式为：  det(A) = %10.3f \n \n", det);  // 输出行列式的值

 

       puts("系数矩阵的逆矩阵为："); // 输出系数矩阵的逆矩阵

 

       for (i=1; i<=n; i++)

       {

              for(j=1; j<=n; j++)

                     printf("%7.3lf", b[i][j]);

              puts("");

       }

 

       puts("\n检验逆矩阵的正确性：\n"); // 输出系数矩阵的逆矩阵

       for(i=1; i<=n; i++)

              for(j=1; j<=n; j++)

              {

                     temp = 0;

                     for(k=1; k<=n; k++)

                            temp += mt[i][k]*b[k][j];  // mt[][] 原系数矩阵

                     c[i][j] = temp;

              }

 

       for (i=1; i<=n; i++)

       {

              for(j=1; j<=n; j++)

                     printf("%7.3lf", c[i][j]);

              puts("");

       }

}