Lagrange插值法的实现——C\Java\Python

Lagrange 插值法

 

一、问题

对于给定的一元函数  的 个节点值 。试用Lagrange公式求其插值多项式或分段三次Lagrange插值多项式。 数据如下：

（1）

xi	0.4	0.55	0.65	0.80	0.95	1.05
yi	0.41075	0.57815	0.69675	0.90	1.00	1.25382

 

求五次Lagrange多项式L₅(x) ，和分段线性插值多项式，计算f(0.96),f(0.99)

 

 

 

　　　　　　　　

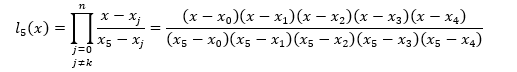
L₅(x)=y₀l₀(x)+y₁l₁(x)+y₂l₂(x)+y₃l₃(x)+y₄l₄(x)+y₅l₅(x)

 

　　　　　　　　　　　　　　　　　　　　　　　　　其中:y0=0.41075,y1=0.57815,y2=0.69675,y3=0.90,y4=1.00,y5=1.25382

 

 

 

 

f(0.96)=1.010051 ,f(0.99)=1.054230

（2）

xi	1	2	3	4	5	6	7
yi	0.368	0.135	0.050	0.018	0.007	0.002	0.001

 试构造Language多项式L6(x),计算f(1.8)的值.(提示:f(1.8≈0.164762）

 

 

 

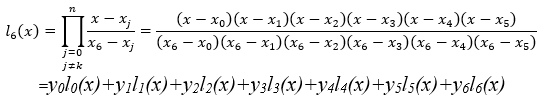
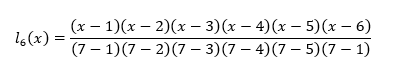
其余与Language多项式L5(x)类似，不多重复

 

二、方法简介

                1、 利用Lagrange插值公式

 

 

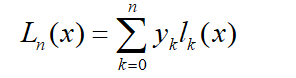
编写出插值多项式程序. 上式中 为插值基函数，

 

 

 

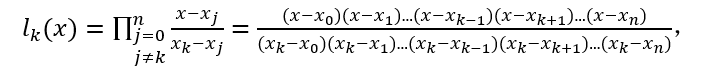
 它满足:

　　　　　　　　

 

 

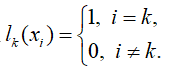
   2、 给出插值多项式或分段线性插值多项式的表达式；

 3、 结合解线性方程组的高斯消法，解下面的线性方程组确定多项式的系数，并对比插值所得结果的异同

 

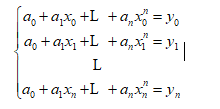
C代码:

//==================================================
#include<stdio.h>
#include<stdlib.h>
#define N 6
double xi[] = {0.4, 0.55, 0.65, 0.80, 0.95, 1.05};    
            //全局变量
double yi[] = {0.41075, 0.57815, 0.69675, 0.90, 1.00, 1.25382};

void main()
{
	double lagrange(double x);
	double x, y;
	FILE *file;
	file = fopen("d:\\data.txt", "w");
	for (x=0.4; x<=1.05; x = x + 0.01)
	{
		y = lagrange(x);
		printf("x = %f, y = %f\n", x, y);
		fprintf(file, "{%f, %f},", x, y);
	}
	fclose(file);
}

double lagrange(double x)
{
	int j, k;
	double y = 0, t, fenzi, fenmu;
	for (k = 0; k <= N-1; k++)
	{
		fenzi = 1;
		fenmu = 1;
		for (j=0; j<=N-1; j++)
		{
			if (j != k)
			{
				fenzi = fenzi * (x - xi[j]);
				fenmu = fenmu * (xi[k] - xi[j]);
			}
		}
		t = yi[k] * fenzi / fenmu;
		y = y + t;
	}
	return y;
}
 //-----------------------------------------------------------

 Java：

import java.util.Scanner;

public class abc {
    public static void main(String args[]){
        Scanner reader =new Scanner(System.in);
        System.out.println("请输待处理的数据长度:");
        int N = reader.nextInt();
        double xi[] = new double[N];
        double yi[] = new double[N];
        System.out.println("请依次输入给定的插值点xi:");
        for(int i = 0;i < xi.length;i++)
        {
            xi[i] = reader.nextDouble();
        }
        System.out.println("请依次输入给定插值点对应的函数值yi:");
        for(int j = 0;j < yi.length;j++)
        {
            yi[j] = reader.nextDouble();
        }
        double x,x2;

        System.out.println("运用拉格朗日插值法解得:");
        for(x=xi[0];x<=xi[xi.length-1];x+=0.01)
        {
            Lagrange M;
            M=new Lagrange(xi,yi,x);
            System.out.printf("f(%4.2f)=%f\t",x,M.pt());
        }
        System.out.println();
        System.out.println("请输入单独求的数值数目为:");
        int Num = reader.nextInt();
        System.out.println("要求的x值为:");
        double x3[]=new double[Num];
        for(int i=0;i<Num;i++){
            x3[i] = reader.nextDouble();
        }
        for(int j=0;j<Num;j++){
            double Num_x=x3[j];
            Lagrange L = new Lagrange(xi,yi,Num_x);
            System.out.println("f("+Num_x+")="+L.pt());
        }
    }
}

class Lagrange{
    int j,k,m,n;
    double fz,fm,x,y =0,t,A[],B[];
    Lagrange(double a[],double b[],double c) {
        m = a.length;
        n = b.length;
        x = c;
        A = a;
        B = b;
    }
    double pt(){
        for(k=0;k<m;k++){
            fz=1;
            fm=1;
            for(j=0;j<n;j++){
                if(j!=k)
                {
                    fz=fz*(x-A[j]);
                    fm=fm*(A[k]-A[j]);
                }
            }
            t = B[k]*fz/fm;
            y = y+t;
        }
        return y;
    }
}

 

 待续...