栈

1. 栈的概念及实现

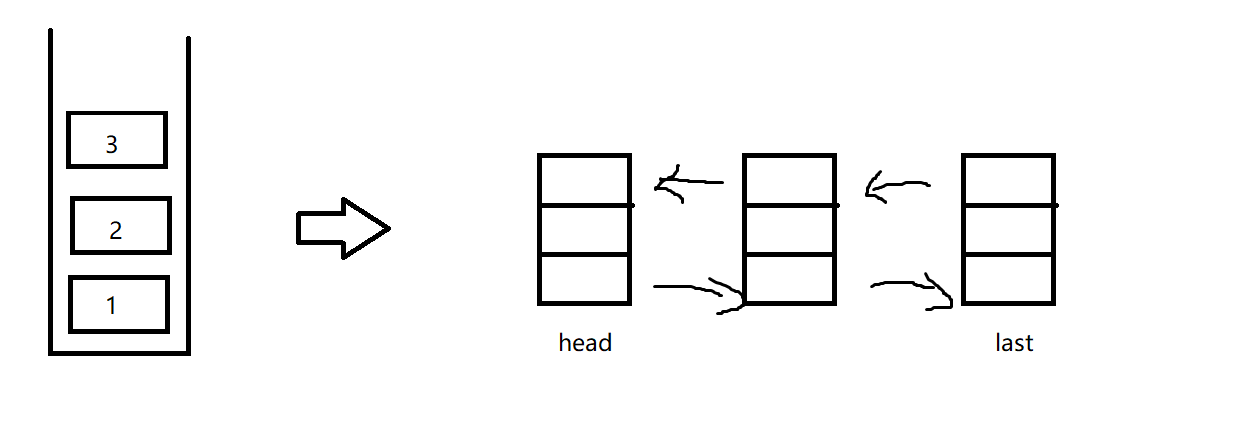
栈是一种先进后出的数据结构，先进后出是指最先入栈的数据最后出栈，最后入栈的数据最先出栈, 如下图

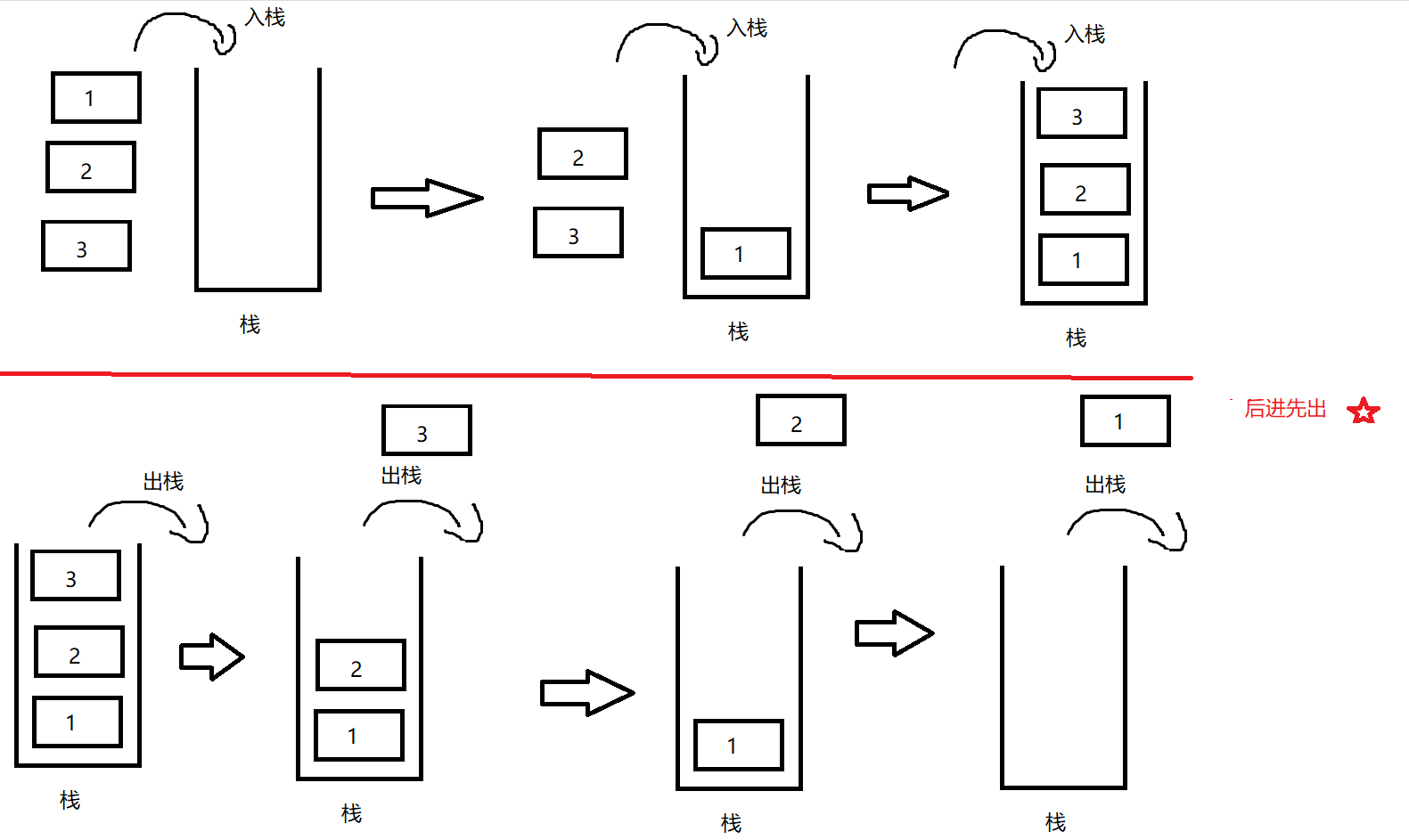
栈的实现:

https://github.com/znxcmakhsd/DS/tree/main/12-18/MyStack

这个栈的实现底层用数组存储数据

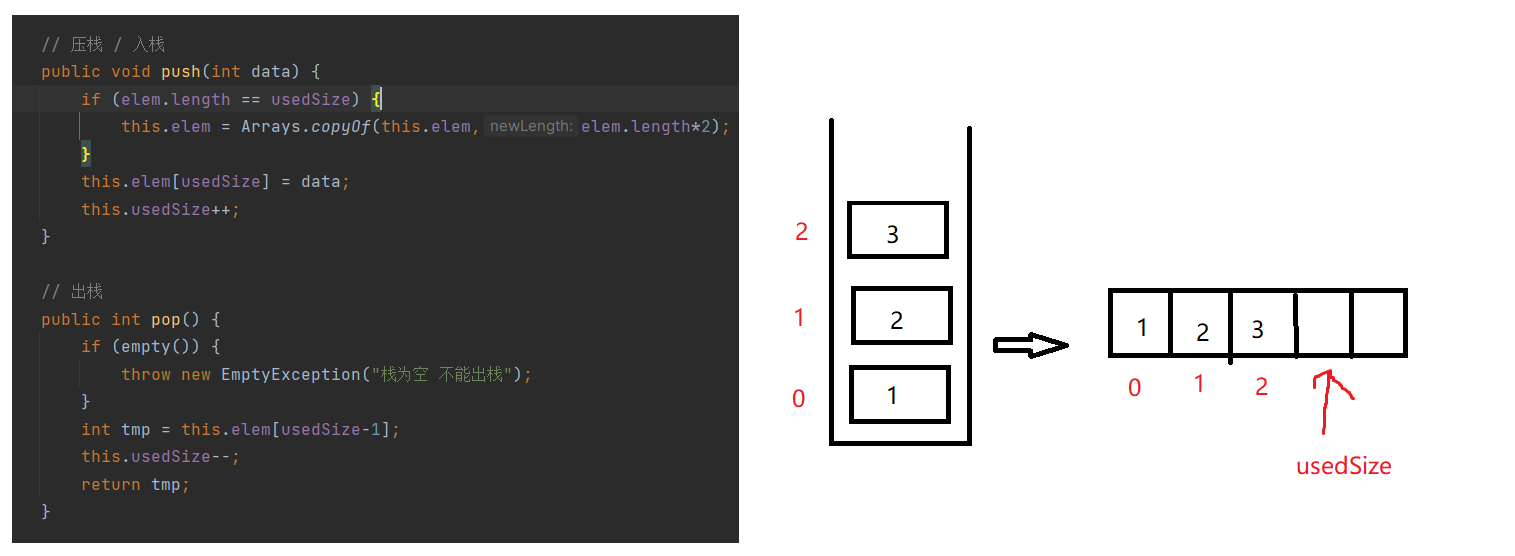
栈也可以用单链表或者是双向链表实现

如果用单链表实现栈，栈的入栈和出栈操作必须是头插/头删, 原因入下

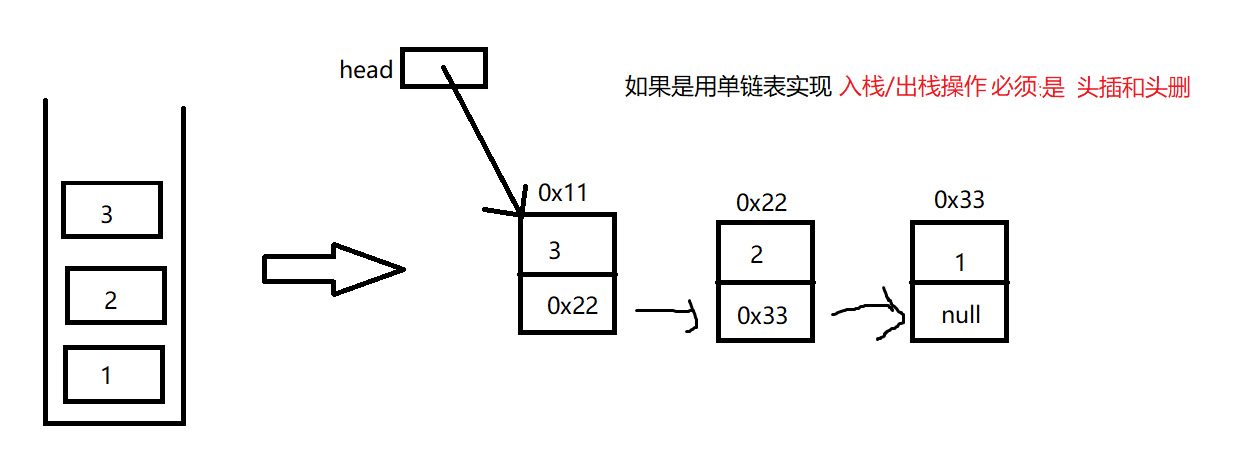
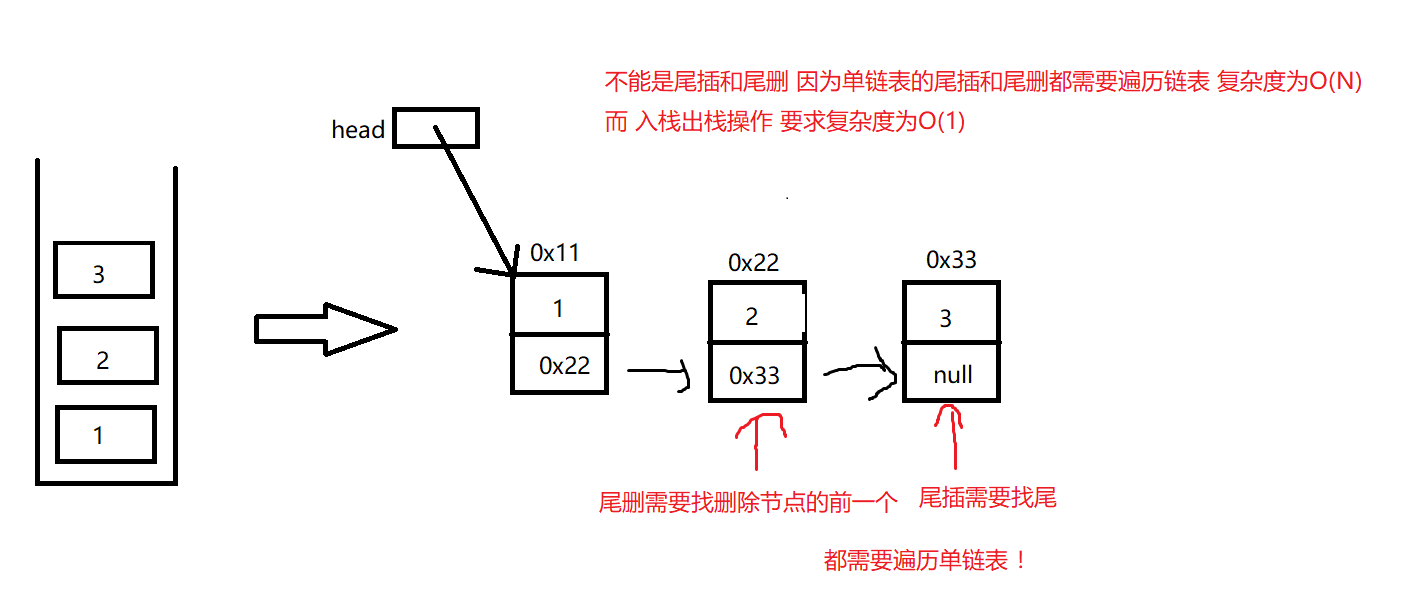
就算给单链表结构加个指向最后节点的引用 尾插可以实现入栈，但是尾删不能实现出栈。

因为尾删需要找到尾节点的前一个, last引用指向尾节点 没办法找到尾节点前面，只能遍历链表

 

如果用双向链表实现，则头插头删 / 尾插尾删都可以实现入栈和出栈操作

因为双向链表有两个引用指向头和尾, 且无论在头还是在尾插入删除数据都只需要修改指向 不需要移动数据，复杂度为O(1）

关于栈的总结:

栈是一个特殊的数据结构，它底层可以用数组或者链表存储数据，但是它组织操作数据方式必须是后进先出

2. 栈的应用

计算后缀表达式结果

什么是后缀表达式 ？

先来看什么是中缀表达式:

( (2 + 1) * 3 )

什么是后缀表达式? 如何将中缀表达式转换为 后缀表达式？

根据运算顺序添加括号，然后将中缀表达式中的运算符移到括号外面，然后去掉所有的括号

 ( (2 + 1) * 3 )   ——运算符移到括号外面 ——》 ( ( 2 1 ) + 3 ) *  ——去掉所有的括号——》 2 1 + 3 *  这个表达式就是一个后缀表达式

 

再来看一个更复杂的例子:

中缀表达式: a + b * c + (d * e + f) * g

先根据运算顺序添加括号: ( (a + (b * c)¹ )² + ( (d * e)³ + f)⁴ * g)⁵ )⁶  注意: 数字表示添加括号的顺序

将运算符移到括号外面：( (a (b c)*¹ )+² ( (de)*³ f)+⁴ g)*⁵ )+⁶

去掉所有的括号: a b c *+ de* f+ g* +

知道了什么是后缀表达式 中缀表达式如何转为后缀表达式后, 再来看如何使用栈计算后缀表达式结果 

class Solution {
    public int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();
        for (int i = 0;i < tokens.length;i++) {
            String str = tokens[i];
            if (!isOperator(str)) {
                // 如果是数字入栈
                int num = Integer.parseInt(str);
                stack.push(num);                
            }else {
                // 是运算符, 出栈计算                
                int right = stack.pop();
                int left = stack.pop();
                switch (str) {
                    case "+":
                        stack.push(left + right);
                        break;
                    case "-":
                        stack.push(left - right);
                        break;
                    case "*":
                        stack.push(left * right);
                        break;
                    case "/":
                        stack.push(left / right);
                        break;    
                }
            }
        }
        return stack.peek();
    }
    private boolean isOperator(String str) {
        if (str.equals("+") || str.equals("-") 
            || str.equals("*") || str.equals("/")) {
                return true;
            }
            return false;
    }
}

括号匹配

class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        for (int i = 0;i < s.length();i++) {
            char ch = s.charAt(i);
            // 左括号入栈
            if (ch == '(' || ch == '['  || ch == '{') {
                stack.push(ch);
            }else {
                // 不匹配情况1: 栈里没有左括号 -> )
                if (stack.empty()) {
                    return false;
                }
                // 左括号与右括号匹配，如果匹配 将左括号出栈准备下一次匹配
                char top = stack.peek();
                if (top == '(' && ch == ')' || top == '[' && ch == ']' || top == '{' && ch == '}') {
                    stack.pop();
                }else {
                    // 不匹配情况2: 左括号与右括号不匹配 -> (]
                    return false;
                }
            }
        }
        // 走到这里表示遍历完了字符串,有两种可能结果
        // 不匹配情况3: 栈里还有左括号 -> (()
        if (!stack.empty()) {
            return false;
        }
        // 遍历完了字符串 同时栈为空, 证明所有括号匹配
        return true;
    }
}

 

判断正确出栈顺序

什么是正确的出栈顺序 ?

若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（）

A: 1,4,3,2  B: 2,3,4,1   C: 3,1,4,2   D: 3,4,2,1

A: 1入 1出 2入 3入 4入 4出 3出 2出  -> 正确  

B:  1入 2入 2出 3入 3出 4入4出 1出  -> 正确  

C: 1入 2入 3入 3出  —> 错误，因为只有先出2才能出1

D: 1入 2入 3入 3出 4入 4出 2出 1出  -> 正确  

这题的解题思路 建议画图走读代码进行理解:

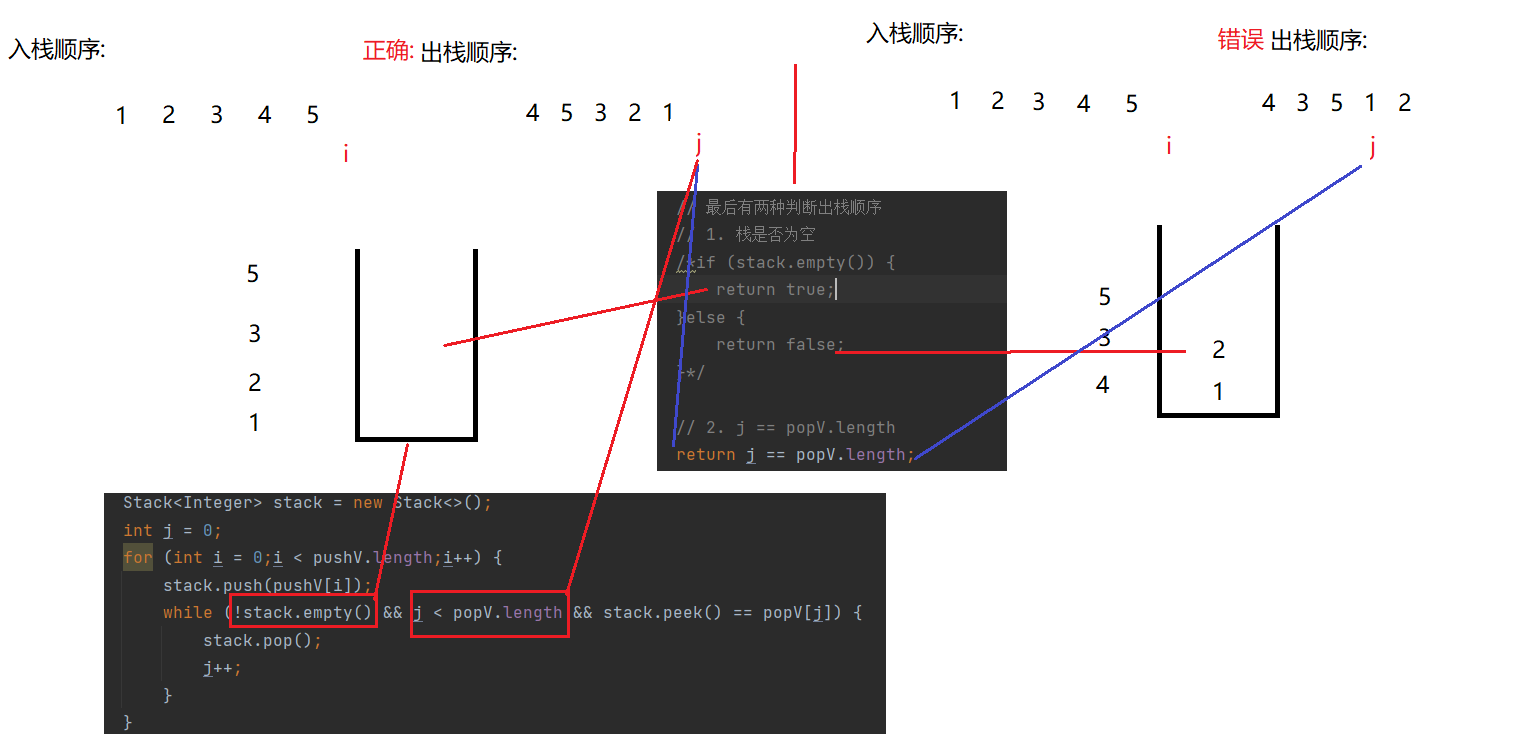
import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param pushV int整型一维数组
     * @param popV int整型一维数组
     * @return bool布尔型
     */
   public static boolean IsPopOrder (int[] pushV, int[] popV) {
        Stack<Integer> stack = new Stack<>();
        int j = 0;
        for (int i = 0;i < pushV.length;i++) {
            stack.push(pushV[i]);
            while (!stack.empty() && j < popV.length && stack.peek() == popV[j]) {
                stack.pop();
                j++;
            }
        }
        // 最后有两种判断出栈顺序
        // 1. 栈是否为空
        /*if (stack.empty()) {
            return true;
        }else {
            return false;
        }*/

        // 2. j == popV.length
        return j == popV.length;
    }
}

最小栈

所以最小栈需要用两个栈实现

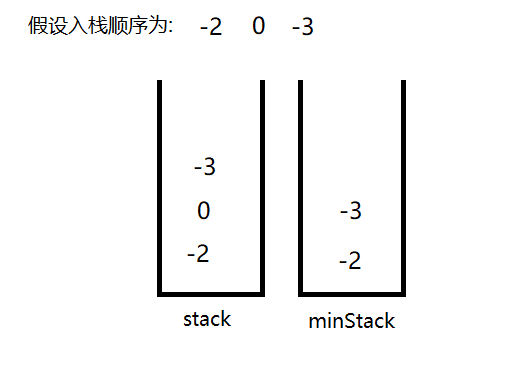
关于最小栈入栈出栈具体的实现思路，建议画图走读下面代码

package MinStack;

import java.util.Stack;

class MinStack {

    public Stack<Integer> stack = new Stack<>();
    public Stack<Integer> minStack = new Stack<>();

    public MinStack() {

    }

    public void push(int val) {
        stack.push(val);
        // 如果最小栈为空, 则直接入栈
        if (minStack.empty()) {
            minStack.push(val);
        }else {
            // 如果最小栈不为空, 比较最小栈栈顶元素与val
            // 如果val小于或者等于栈顶元素 入栈
            if (val < minStack.peek()) {
                minStack.push(val);
            }
        }
    }

    // 删除栈顶元素
    public void pop() {
        // 普通栈肯定是要出栈
        // 如果普通栈出栈的元素 与 最小栈栈顶元素一样
        // 则最小栈出栈, 因为出栈的会是最小元素
        int top = stack.pop();
        if (top == minStack.peek()) {
            minStack.pop();
        }
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */