数论进阶刷题柱
洛谷P3383 线性筛素数
线性筛,那很模板了
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1000010;//1e9+7;
ll read(){ll x;scanf("%lld",&x);return x;}
ll quick(ll a,ll b,ll mod){ll t=1;while(b){if(b&1)t=t*a%mod;b=b/2;a=a*a%mod;}return t;}
int lowbit(int x){return x&(-x);}
int pri[6000000],v[100000010],cnt;
void work()
{
cout<<pri[read()]<<'\n';
}
int main()
{
// freopen("queue.in","r",stdin);
// freopen("queue.out","w",stdout);
int n=read();
for(int i=2;i<=n;i++)
{
if(v[i]==0){
pri[++cnt]=i;
v[i]=i;
}
for(int j=1;1ll*i*pri[j]<=n&&j<=cnt&&pri[j]<=v[i];j++)
v[i*pri[j]]=i;
}
for(int t=read();t;t--)
work();
}
洛谷P4774 [NOI2018] 屠龙勇士
每次选择的剑的攻击力可以用\(multiset\)得到,设为\(b[i]\)。
接下来的任务是求\(x\)满足\(n\)个同余方程:\(b[i]*x\equiv a[i] \% p[i]\),类似于acwing 204 ,我们做\(n\)次扩欧。
具体来说,对于单个同余方程\(b[i]*x \equiv a[i]\% p[i]\),他的特解如果是\(x0\),通解为\(x0+k*{p[i]\over \gcd(p[i],b[i])}\)
那么对于多个同余方程,设\(x\)表示前\(i\)个方程的一个特解,初始值为\(0\)。设\(M\)表示前\(i\)个方程的\({p[i]\over \gcd(p[i],b[i])}\)的\(lcm\),初始值为\(1\)。前\(i\)个方程的通解即为\(x+kM\)。
已有前\(i-1\)个方程的特解,为了求前\(i\)个方程的特解,你需要求\((x+t*M)*b[i] \equiv a[i] \% p[i]\)的\(t\)的一个特解,那么\((x+t*M)\)就是前\(i\)个方程的特解。
等价于\(t*M*b[i] \equiv a[i]-x*b[i]\ \% p[i]\)。他的通解是\(t=t0+k*{p[i]\over gcd(M*b[i],p[i])}\)
做\(exgcd\)的时候有一步不得不用龟速乘或者int128,其他地方用\(ll\)即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010;//1e9+7;
ll read(){ll x;scanf("%lld",&x);return x;}
ll quick(ll a,ll b,ll mod){ll t=1;while(b){if(b&1)t=t*a%mod;b=b/2;a=a*a%mod;}return t;}
int lowbit(int x){return x&(-x);}
ll a[N],b[N],jiang[N],p[N];
multiset<ll>o;
ll exgcd(ll A,ll B,ll &x,ll &y)
{
if(B==0)
{
x=1,y=1;return A;
}
ll d=exgcd(B,A%B,x,y);
ll z=x;
x=y;y=z-y*(A/B);
return d;
}
ll ask(ll A,ll B,ll c)//1e18,1e12,1e18
{
ll x,y;
ll gcd=exgcd(A,B,x,y);
if(c%gcd)
return -1;
B=B/gcd;c=c/gcd;
x=((__int128)c*x%B+B)%B;
return x;
}
void work()
{
o.clear();
int n=read(),m=read();
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
p[i]=read();
for(int i=1;i<=n;i++)
jiang[i]=read();
for(int i=1;i<=m;i++)
o.insert(read());
ll maxx=0;//维护每个龙至少要砍多少刀
//答案要等于等于maxx
for(int i=1;i<=n;i++)
{
if(*o.begin()>a[i])//全都大于
b[i]=*o.begin();
else
{
auto t=o.upper_bound(a[i]);
t--;
b[i]=*t;
}
//砍i龙选择的剑的攻击力为b
maxx=max(maxx,(a[i]+b[i]-1)/b[i]);
o.erase(o.find(b[i]));
o.insert(jiang[i]);//把奖励的剑加上
}
ll M=1;ll x=0;
for(int i=1;i<=n;i++)
{
ll t=ask(M*b[i]%p[i],p[i],(a[i]-x*b[i])%p[i]);
if(t==-1){
cout<<"-1\n";
return ;
}
x=x+t*M;
p[i]=p[i]/__gcd(p[i],b[i]);
M=M/__gcd(M,p[i])*p[i];
x=x%M;
}
x=(x%M+M)%M;
if(x<maxx)
x=x+(maxx-x+M-1)/M*M;
cout<<(ll)x<<'\n';
}
int main()
{
for(int t=read();t;t--)
work();
}
BZOJ3884. 上帝与集合的正确用法
请看基础数论刷题柱。
洛谷P9007 最澄澈的空与海 (Hard Version)
1、\(x=(n-1)!(n-1)*{z\over z-1}\)
z-1是(n-1)!(n-1)的因数即可。
2、y=x-z*(n-1)!,因此确定z之后x和y同时确定了,答案就是\((n-1)!(n-1)\)的因子数量
求因子数量可以质因数分解,\(\prod 幂次+1\)即为所求。
对于每次询问独立处理,复杂度是\(T*1\sim n的质数数量*logn\)。
但是我们考虑先对每个n求一下答案,询问的时候o1输出即可。预处理的时候维护\((n-1)!\),然后加上\((n-1)\),得到答案,再退掉\((n-1)\)即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010,mod=998244353;
ll read(){ll x;scanf("%lld",&x);return x;}
ll quick(ll a,ll b){ll t=1;while(b){if(b&1)t=t*a%mod;b=b/2;a=a*a%mod;}return t;}
int lowbit(int x){return x&(-x);}
int pri[1000010],v[1000010],m,cnt[1000010],now,f[1000010];
void add(int x,int k)
{
while(x!=1)
{
int p=v[x];
now=now*quick(1+cnt[p],mod-2)%mod;
while(x%p==0)
{
cnt[p]+=k;
x=x/p;
}
now=now*(1ll+cnt[p])%mod;
}
}
int main()
{
for(int i=2;i<=1000000;i++)//预处理v[i]表示i的最小质因子,便于后续快速质因数分解
{
if(v[i]==0){
pri[++m]=i;
v[i]=i;
}
for(int j=1;j<=m;j++){
if(pri[j]>v[i]||pri[j]>1000000/i)
break;
v[i*pri[j]]=pri[j];
}
}
now=1;
for(int i=2;i<=1000000;i++)
{
add(i-1,1);
//此时是(i-1)!
add(i-1,1);
//此时是(i-1)!(i-1)
f[i]=now;
add(i-1,-1);
}
for(int t=read();t;t--){
int n=read();
if(n==1)
cout<<"inf\n";
else
cout<<f[n]<<'\n';
}
}
洛谷P2480 古代猪文
请看基础数论刷题柱
BZOJ2749 [HAOI2012] 洛谷P2350 外星人
请看基础数论刷题柱
洛谷P5495 Dirichlet 前缀和
看一眼式子,我会调和级数\(O(nlogn)\)!
输入\(2e7\)发现跑了\(4s\),所以换个方法。
高维前缀和之前备课过,所以,掏出高维前缀和的图:
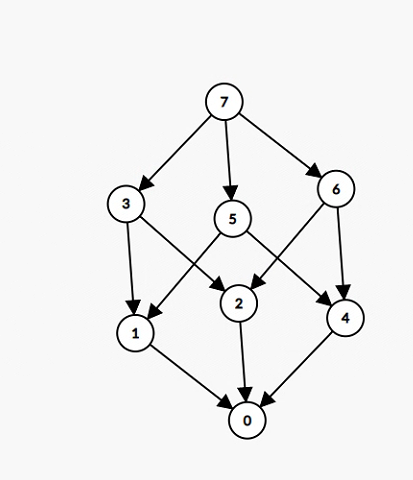
高维前缀和如果贡献是走二进制的子集可以枚举二进制的每一位进行转移。
如果走的是质数的子集也可以枚举每个质数进行转移。
具体来说,先预处理出所有质数,再枚举质数\(pri[i]\),用\(a[j]\)去更新\(a[j*pri[i]]\),即可做到正确转移。
举例\(n=10\):
刚开始每个\(a_i\)只有初始的\(a_i\)(话说这个图好像离散数学里学过,叫什么什么图)
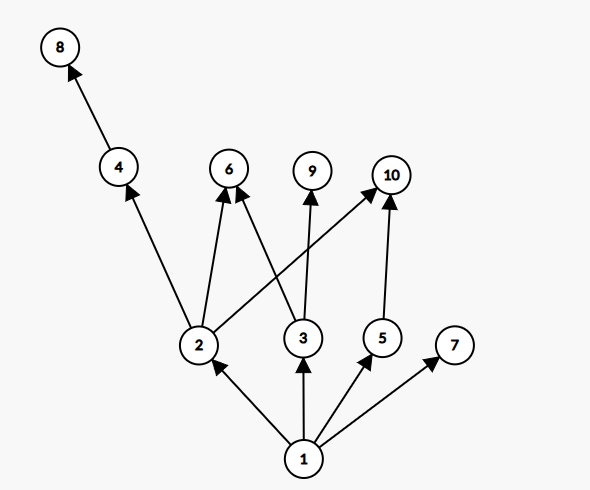
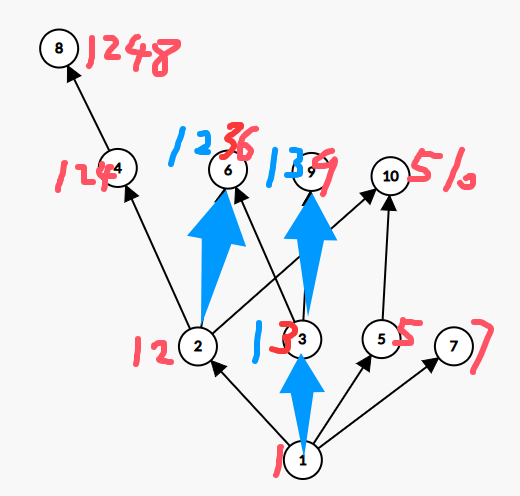
用\(2\)做一次转移后:

用\(3\)做一次转移后:
用\(5\)做一次转移后:
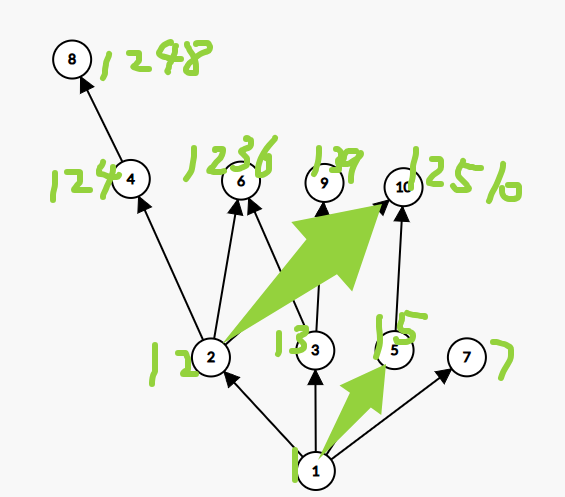
用7做转移就不画了,唯一改变了的是\(a[7]\)会变成\(a[1]+a[7]\)。
唉唉,感觉画得太好了,高手。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned int uint;
uint seed;
uint getnext(){
seed^=seed<<13;
seed^=seed>>17;
seed^=seed<<5;
return seed;
}
const int N=20000010,mod=998244353;
ll read(){ll x;scanf("%lld",&x);return x;}
ll quick(ll a,ll b){ll t=1;while(b){if(b&1)t=t*a%mod;b=b/2;a=a*a%mod;}return t;}
int lowbit(int x){return x&(-x);}
int n;
uint a[N],ans;
int v[N],pri[N],cnt;
int main()
{
n=read();
cin>>seed;
for(int i=1;i<=n;i++)
a[i]=getnext();
for(int i=2;i<=n;i++)
{
if(v[i]==0)
{
pri[++cnt]=i;
v[i]=i;
}
for(int j=1;j<=cnt;j++)
{
if(pri[j]>v[i]||pri[j]>n/i)
break;
v[i*pri[j]]=pri[j];
}
}
for(int i=1;i<=cnt;i++)
for(int j=1;j*pri[i]<=n;j++)
a[j*pri[i]]+=a[j];
for(int i=1;i<=n;i++)
ans=ans^a[i];
cout<<ans;
}
BZOJ2705 洛谷P2303 Longge的问题
请看基础数论刷题柱。
BZOJ2005 [Noi2010] 洛谷P1447 能量采集
参考于victorique的博客
看起来类似仪仗队
对于互质的xy,计算答案如何呢
考虑1~1e5的\(\sum_{i=1}^{10^5} \varphi(i)\)比较大,已经3e9了。
枚举互质的\(x,y\),答案是
\(\sum min({n\over x},{m\over y})^2\):\(min({n\over x},{m\over y})\)的含义是在\(x,y\)的延长线上的一共有几个点,贡献是平方,但是做下来比较困难。考虑换个角度,答案也可以表示为\(\sum\limits_{i\in1\sim n,j\in 1\sim m} 2*gcd(i,j)-1\)
接下来设\(n<m\)
\(ans=\sum\limits_{i=1}^n\sum\limits_{j=1}^m(2*gcd(i,j)-1)\)
\(2*\sum\limits_{i=1}^n\sum\limits_{j=1}^m gcd(i,j) -2*n*m\)
关注这个\(\sum\limits_{i=1}^n\sum\limits_{j=1}^m gcd(i,j)\)
枚举\(gcd\)的值为\(d\),他的贡献为\(gcd\)恰好为\(d\)的\(ij\)数量
=\(\sum\limits_{d=1}^nd\sum\limits_{i=1}^n \sum\limits_{j=1}^m[gcd(i,j)=d]\)
使用莫比乌斯反演,\(gcd(i,j)=d\)的数量为\(gcd\)为\(d\)的倍数的数量\(-gcd\)为\(2d\)的倍数的数量\(-gcd\)为\(3d\)的倍数的数量\(-gcd\)为\(5d\)的倍数的数量\(+gcd\)为\(6d\)的倍数的数量...,对于\(d\)的整数倍\(T\)倍,这个容斥系数是\(\mu (T\over d)\),\(gcd\)为\(T\)的倍数的数量是\({n\over T}\times {m\over T}\),\(T\)的范围是\(1\sim n \and d|T\)
\(=\sum\limits_{d=1}^nd\sum\limits_{d|T}^{n} \mu({T\over d}) {n\over T} {m\over T}\)
让\(d\)进到内部\(\sum\)里
\(=\sum\limits_{d=1}^n\sum\limits_{d|T}^{T\leq n} d \mu({T\over d}) {n\over T} {m\over T}\)
交换\(\sum\)顺序,这样T的范围是\(1\sim n\),\(d\)的范围是\(d | T\)
\(=\sum\limits_{T=1}^n\sum\limits_{d|T}d \mu({T\over d}) {n\over T} {m\over T}\)
此时\({n\over T}{m\over T}\)和d无关,可以放到外部\(\sum\)里
$=\sum\limits_{T=1}^n {n\over T} {m\over T} \sum\limits_{d|T}d \mu({T\over d}) $
根据\(\varphi=id*\mu\),\(\sum\limits_{d|T}d\mu({T\over d})\)可以变化为\(\varphi (T)\)
\(=\sum\limits_{T=1}^n {n\over T} {m\over T} \varphi(T)\)
可以\(O(n\sqrt n)\)枚举T,暴力计算欧拉函数来做,也可以预处理欧拉函数优化之。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned int uint;
uint seed;
const int N=1000110,mod=998244353;
ll read(){ll x;scanf("%lld",&x);return x;}
ll quick(ll a,ll b){ll t=1;while(b){if(b&1)t=t*a%mod;b=b/2;a=a*a%mod;}return t;}
int lowbit(int x){return x&(-x);}
int v[N],pri[N],cnt,phi[N];
ll n,m,ans;
int main()
{
n=read();m=read();
if(n>m)
swap(n,m);
phi[1]=1;
for(int i=2;i<=n;i++){
if(v[i]==0)
{
pri[++cnt]=i;
v[i]=i;
phi[i]=i-1;
}
for(int j=1;j<=cnt;j++)
{
if(pri[j]>v[i]||pri[j]>n/i)
break;
v[i*pri[j]]=pri[j];
if(i%pri[j])
phi[i*pri[j]]=phi[i]*(pri[j]-1);
else
phi[i*pri[j]]=phi[i]*pri[j];
}
}
for(int T=1;T<=n;T++)
ans=ans+(n/T)*(m/T)*phi[T];
cout<<ans*2-n*m;
}
洛谷P3911 最小公倍数之和
\(\sum\limits_{i=1}^N\sum\limits_{j=1}^Nlcm(a_i,a_j)\)
\(=\sum\limits_{i=1}^N\sum\limits_{j=1}^N{a_i*a_j\over gcd(a_i,a_j)}\)
枚举\(gcd(a_i,a_j)\)值为\(d\),则\(d\)的贡献是全体\(gcd(a_i,a_j)=d\)的\(a_i,a_j\)的乘积之和除以\(d\)。
\(=\sum\limits_{d=1}^{5e4} {1\over d}\sum\limits_{i=1}^n\sum\limits_{j=1}^m a_i*a_j[gcd(a_i,a_j)=d]\)
接下来算这个"全体\(gcd(a_i,a_j)=d\)的\(a_i,a_j\)的乘积之和"
如果直接去算,看起来乘积之和可以转换成和的乘积,但是不一定可行。比如\(2,4,6,8\),\(d=2\)的时候,答案是\(2*2+2*4+2*6+2*8+4*2+4*6+6*2+6*4+6*8+8*2+8*6\)。
看起来\(2,4,6,8\)都有涉猎,但是不一定全都在。我们用和的乘积\((2+4+6+8)*(2+4+6+8)\)得到的是\(gcd=2的倍数的a_i,a_j乘积之和\)。
我们应该用 \(gcd=d的倍数的a_i,a_j乘积之和\) 减去 \(gcd=2d的a_i,a_j乘积之和\) 减去 \(gcd=3d的a_i,a_j乘积之和\)...这个可以枚举d的整数倍进行容斥。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned int uint;
uint seed;
const int N=1000110,mod=998244353;
ll read(){ll x;scanf("%lld",&x);return x;}
ll quick(ll a,ll b){ll t=1;while(b){if(b&1)t=t*a%mod;b=b/2;a=a*a%mod;}return t;}
int lowbit(int x){return x&(-x);}
int v[N],pri[N],cnt,phi[N];
ll n,m,ans,sum[N];
int main()
{
n=read();
for(int i=1;i<=n;i++)
{
int v=read();
sum[v]+=v;
}
//此时sum[v]表示v*v的出现次数
for(int i=1;i<=50000;i++)
for(int j=i+i;j<=50000;j+=i)
sum[i]+=sum[j];//此时sum[i]表示i的倍数的数字之和
for(int i=50000;i>=1;i--)
{
sum[i]=sum[i]*sum[i];
//此时sum表示i的倍数的数字之和的平方
//也就是满足gcd(ai,aj)=i的倍数的Σai*aj
for(int j=i+i;j<=50000;j+=i)
sum[i]-=sum[j];
//容斥后,此时sum[i]表示满足gcd(ai,aj)恰好=i的Σai*aj
ans=ans+sum[i]/i;//把sum[i]/i计算到答案里
}
cout<<ans;
}
简单题
首先要学习一个前置知识:设\(S(x)=\sum\limits_{i=1}^x \sum\limits_{j=1}^x(i+j)^k\),\(F(x)=\sum\limits_{i=1}^x i^k\),\(G(x)=\sum\limits_{i=1}^nF(i)\),则有\(S(x)=G(2x)-2G(x)\)
对于质数暴力计算\(i^k\),非质数需要在线性筛里算出来\(i^k\),然后做一次前缀和得到\(f[x]\),再做一次前缀和可以得到\(g[x]\),然后减一减可以得到\(s[x]\)。
接下来和上一题很一样了,枚举那些无平方因子的\(d\),则\(gcd(i,j)=d的倍数\)的\(i,j\)的\(\sum (i+j)^k=s[n/d]*quick(d,k)\),有了\(d\)的倍数的答案,接下来枚举的\(d\)倍数容斥一下可以得到\(gcd(i,j)\)恰好\(=d\)的\(\sum (i+j)^k\),这个再乘\(d\)累加给\(ans\)即可。
为了卡常,原本应该线性筛筛出来\(f[x]=i^k\)然后开始做两次前缀和的,我的代码里没有做前缀和,让他保留\(f[x]=i^k\),这样接下来算答案的时候不需要再算\(i^k\)了。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned int uint;
uint seed;
const int N=10000010,mod=998244353;
ll read(){ll x;scanf("%lld",&x);return x;}
int quick(int a,ll b){int t=1;if(b>=mod)b=b%(mod-1)+mod-1;while(b){if(b&1)t=(ll)t*a%mod;b=b/2;a=(ll)a*a%mod;}return t;}
int v[N],pri[N],cnt,F[N],flag[N];
ll k;
int n,ans,sum[N],f[N],g[N],s[N];
int main()
{
n=read();k=read();
f[1]=1;
for(int i=2;i<=2*n;i++)
{
if(v[i]==0)
{
v[i]=i;
pri[++cnt]=i;
f[i]=quick(i,k);
}
for(int j=1;j<=cnt;j++)
{
if(pri[j]>v[i]||pri[j]>2*n/i)
break;
v[i*pri[j]]=pri[j];
f[i*pri[j]]=(ll)f[i]*f[pri[j]]%mod;
}
}
for(int i=1;i<=2*n;i++)
g[i]=(g[i-1]+f[i])%mod;
for(int i=1;i<=2*n;i++)
g[i]=(g[i-1]+g[i])%mod;
for(int i=1;i<=n;i++)
s[i]=(g[2*i]-2ll*g[i]+2*mod)%mod;
for(int i=1;i<=cnt;i++)
{
if(1ll*pri[i]*pri[i]>n)
break;
pri[i]=pri[i]*pri[i];
for(int j=pri[i];j<=n;j+=pri[i])
flag[j]=1;
}
for(int d=n;d>=1;d--)
{
F[d]=(ll)s[n/d]*f[d]%mod;//gcd是d的倍数的
for(int i=d+d;i<=n;i+=d)
F[d]=(F[d]-F[i])%mod;
if(flag[d])
continue;
//gcd恰好是d的
ans=(ans+1ll*F[d]*d)%mod;
}
cout<<(ans+mod)%mod;
}
洛谷 U581141 网格(grid)
知难而退,跳过去了
洛谷P3327 [SDOI2015] 约数个数和
\(\sum\limits_{i=1}^n \sum\limits_{j=1}^m d(i,j)\)
对于因子X,考虑质因子的分配情况:设X的质因子只在i里出现的设为x,只在j里出现的设为y,则这样的因子\(k*x*y\)有\({n\over x}{m\over y}\)个,对答案的贡献也是\({n\over x}{m\over y}\)。
\(=\sum\limits_{x=1}^n \sum\limits_{y=1}^m [gcd(x,y)=1]{n\over x}{m\over y}\)
莫比乌斯反演
设\(f(x)=\sum_{k=1}^x {x\over k}\)
提前预处理计算\(f(x)\),内部可以使用整除分块,预处理复杂度为\(O(n\sqrt n)\)。
\(g(d)=\sum\limits_{x=1}^n \sum\limits_{y=1}^m [d|gcd(x,y)]{n\over x}{m\over y}\)
\(=\sum\limits_{x=1}^n [d|x]{n\over x}\sum\limits_{y=1}^m [d|y]{m\over y}\)
\(d|gcd(x,y)\)说明x和y都是d的倍数(充分必要)
\(=(\sum\limits_{k=1}^{n/d}{n/d\over k})(\sum\limits_{k=1}^{m/d}{m/d\over k})\)
\(=f(n/d)*f(m/d)\)
\(ans=\sum\limits_{d=1}^n\mu(d)g(d)\),暴力可以做到\(O(Tn)\)。
使用整除分块,对于\(n/d,m/d\)值相同的\(d\in[l,r]\),他的\(g(d)\)值相同,可以预处理\(\mu(d)\)的前缀和来加速。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned int uint;
uint seed;
const int N=50010,mod=998244353;
ll read(){ll x;scanf("%lld",&x);return x;}
int quick(int a,ll b){int t=1;if(b>=mod)b=b%(mod-1)+mod-1;while(b){if(b&1)t=(ll)t*a%mod;b=b/2;a=(ll)a*a%mod;}return t;}
int n,m;
ll ans,f[N],mu[N];
int askmu(int x)
{
int cnt=0,maxx=sqrt(x);
for(int i=2;i<=maxx;i++)
{
if(x%i==0)
{
cnt++;
if(x/i%i==0)
return 0;
while(x%i==0)
x=x/i;
}
}
if(x!=1)
cnt++;
if(cnt%2==0)
return 1;
else
return -1;
}
ll g(int d)
{
return f[n/d]*f[m/d];
}
int main()
{
for(int x=1;x<=50000;x++)
{
for(int l=1,r;l<=x;l=r+1)
{
r=x/(x/l);
f[x]=f[x]+(r-l+1)*(x/l);
}
mu[x]=mu[x-1]+askmu(x);
}
for(int t=read();t;t--)
{
ans=0;
n=read();m=read();
if(n>m)
swap(n,m);
for(int l=1,r;l<=n&&l<=m;l=r+1)
{
r=min(n/(n/l),m/(m/l));
ans=ans+(mu[r]-mu[l-1])*g(l);
}
cout<<ans<<'\n';
}
}
杜教筛
求积性函数\(f(n)\)的前缀和\(S(n)=\sum\limits_{i=1}^n f(i)\)
找一个积性函数\(g\),狄利克雷卷积前缀和为:
\(\sum\limits_{i=1}^n(f*g)(i)\)
根据狄利克雷卷积的定义
\(=\sum\limits_{i=1}^n\sum\limits_{d|i}f(i/d)g(d)\)
交换枚举顺序
\(=\sum\limits_{d=1}^n\sum\limits_{d|i}f(i/d)g(d)\)
从枚举\(i\)变为枚举\(i\)是\(d\)的\(k\)倍
\(=\sum\limits_{d=1}^n\sum\limits_{k=1}^{n/d}f(k)g(d)\)
把\(g(d)\)拿出来
\(=\sum\limits_{d=1}^ng(d)\sum\limits_{k=1}^{n/d}f(k)\)
发现内部正是\(S(n/d)\)
\(=\sum\limits_{d=1}^ng(d)S(n/d)\)
相求的是\(S(n)\),因为\(g\)是积性函数,因此\(g(1)=1\)
\(g(1)S(n)\)
作为狄利克雷卷积前缀和的第一项,等于全体前缀和-其他项
\(=\sum\limits_{d=1}^ng(d)S(n/d)-\sum\limits_{d=2}^ng(d)S(n/d)\)
\(=\sum\limits_{i=1}^n(f*g)(i)-\sum\limits_{d=2}^ng(d)S(n/d)\)
第二个式子和上一题的最后一步
\(ans=\sum\limits_{d=1}^n\mu(d)g(d)=\sum\limits_{d=1}^n\mu(d)f(n/d)*f(m/d)\)很像,尝试使用整除分块:如果能快速求得\(\sum_{i=1}^n(f*g)(i)\)和\(\sum\limits_{d=l}^rg(d)\),那么就可以递归地去求\(S(n/i)\),复杂度可以降到\(O(n^{3\over 4})\)。
使用大步小步可以优化到\(O(n^{2/3})\)。
本题第一问:\(\varphi\)的前缀和
我们有\(\varphi*I=id\),说的是
\((\varphi*I)(x)=\sum\limits_{i|x}\varphi(i)*I(x/i)\)
因为\(I(n)=1\)
\(=\sum\limits_{i|x}\varphi(i)\)
根据蓝书“互质与欧拉函数”那一章欧拉函数的第六条性质\(\sum\limits_{d|n}\varphi(d)=n\)
\(=n\)
根据\(id(n)=n\)
\(=id(n)\)
这样开始用杜教筛递归地求欧拉函数的前缀和,此时\(\sum_{i=1}^n(f*g)(i)\)是\(1+2+3+...+n=(1+n)*n/2\),\(\sum\limits_{d=l}^rg(d)\)是\((1+1+1+...+1)=(r-l+1)\)。
本题第二问:\(\mu\)的前缀和
我们有\(\mu*I=\varepsilon\),说的是\((\mu*I)(x)=\sum\limits_{i|x}\mu(i)*I(x/i)=\sum\limits_{i|x}\mu(i)\)
当\(x\)是\(1\),\(\sum\limits_{i|x}\mu(i)=\mu(1)=1\),满足条件。
当\(x\)不是\(1\),不同质因子的组合情况,根据二项式定理一定是\(0\)
这样开始用杜教筛递归地求欧拉函数的前缀和,此时\(\sum_{i=1}^n(f*g)(i)\)是\(1+0+0+...+0=1\),\(\sum\limits_{d=l}^rg(d)\)是\((1+1+1+...+1)=(r-l+1)\)。
代码实现的时候,推荐整除分块的\(l,r\)使用\(ll\)类型,避免\(l=r+1\)的时候爆\(int\)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2000010,mod=998244353;
ll read(){ll x;scanf("%lld",&x);return x;}
int quick(int a,ll b){int t=1;if(b>=mod)b=b%(mod-1)+mod-1;while(b){if(b&1)t=(ll)t*a%mod;b=b/2;a=(ll)a*a%mod;}return t;}
map<int,ll>phi,mu;
int v[N],pri[N],m;
ll phi0[N],mu0[N];
ll askphi(int n)
{
if(n<=2000000)
return phi0[n];
if(phi.count(n))
return phi[n];
ll ans=(1ll+n)*n/2;
for(ll l=2,r;l<=n;l=r+1)
{
r=n/(n/l);
ans=ans-(r-l+1)*askphi(n/l);
}
return phi[n]=ans;
}
ll askmu(int n)
{
if(n<=2000000)
return mu0[n];
if(mu.count(n))
return mu[n];
ll ans=1;
for(ll l=2,r;l<=n;l=r+1)
{
r=n/(n/l);
ans=ans-(r-l+1)*askmu(n/l);
}
return mu[n]=ans;
}
void work()
{
int n=read();
cout<<askphi(n)<<' '<<askmu(n)<<'\n';
}
void workmu(int i)
{
int x=i;
mu0[i]=1;//假装是0
while(x!=1)
{
if(x/v[x]%v[x]==0)//有平方因子
{
mu0[i]=0;
return ;
}
x=x/v[x];
mu0[i]=-mu0[i];
}
}
main()
{
phi0[1]=1;
for(int i=2;i<=2000000;i++)
{
if(v[i]==0){
v[i]=i;
pri[++m]=i;
phi0[i]=i-1;
}
for(int j=1;j<=m;j++)
{
if(pri[j]>v[i]||pri[j]>2000000/i)
break;
v[i*pri[j]]=pri[j];
if(i%pri[j])
phi0[i*pri[j]]=phi0[i]*(pri[j]-1);
else
phi0[i*pri[j]]=phi0[i]*pri[j];
}
phi0[i]=phi0[i-1]+phi0[i];
}
for(int i=1;i<=2000000;i++)
{
workmu(i);
mu0[i]=mu0[i-1]+mu0[i];
}
for(int t=read();t;t--)
work();
}
简单的数学题
\(\sum\limits_{i=1}^n \sum\limits_{j=1}^n ijgcd(i,j)\)
设\(gcd(i,j)=k\),众所周知,\(\sum\limits_{d|k}\varphi(d)=k\)(蓝书欧拉函数性质\(6\)),因此\(gcd(i,j)=\sum\limits_{d|k}\varphi(d)=k=\sum\limits_{d|i\and d|j}\varphi(d)=k\)
\(=\sum\limits_{i=1}^n \sum\limits_{j=1}^n ij\sum\limits_{d|i\and d|j}\varphi(d)\)
枚举\(d\),计算\(\varphi(d)\)对答案的贡献可以算他的出现次数,是\(1\sim n\)的\(k\)的倍数的\(i\)和\(k\)的倍数的\(j\)的\(\sum ij\),枚举\(i\)是\(d\)的\(x\)倍,\(j\)是\(d\)的\(y\)倍,则原来的\(ij\)变成\(xyd^2\)
\(=\sum\limits_{d=1}^n\varphi(d)\sum\limits_{x=1}^{n/d}\sum\limits_{y=1}^{n/d}xyd^2\)
把d^2拿出来,里面的\(\sum\sum xy\)也不困难
\(=\sum\limits_{d=1}^n\varphi(d)d^2(\sum\limits_{x=1}^{n/d}x)^2\)
由于\((\sum\limits_{i=1}^ni)^2=\sum\limits_{i=1}^ni^3\)
\(=\sum\limits_{d=1}^n\varphi(d)d^2\sum\limits_{x=1}^{n/d}x^3\)
此时能做到\(O(n)\),看一眼数据天塌了,怎么\(n\)是\(10^{10}\)。
作为杜教筛高手,我们求助于\(\varphi*I=id\),来快速求得\(phi\)的前缀和,有了前缀和就可以开始整除分块了。对于一个\(n/d\)的商相同的区间\([l,r]\),计算他的答案,此时\(\sum\limits_{x=1}^{n/d}x^3\)是一个固定值,\(\varphi(d)\)和\(d^2\)在变化,而我只会求\(\varphi(d)\)的前缀和,不会求\(\varphi(d)*d^2\)的前缀和。
\(=\sum\limits_{d=1}^n\varphi(d)d^2(\sum\limits_{x=1}^{n/d}x)^2\)
设\(f(i)=\varphi(d)*d^2\),要求的是\(S(n)=\sum\limits_{i=1}^nf(i)\),找一个\(g(i)={i^2}\),这样卷积一下\((f*g)(i)=\sum\limits_{d|i}\varphi(d)*d*d*(i/d)*(i/d)=\sum\limits_{d|i}\varphi(d)*i^2=i^3\),至此我们能够快速求得\(\sum\limits_{i=1}^n(f*g)(i)\)和\(\sum\limits_{d=l}^rg(d)\),感觉差不多了!
写了个无记忆化的发现跑不出来,加上记忆化发现\(mod=998244353,n=10^9\)能在9s后正确输出\(380165988\)。考虑预处理\(\varphi\)再预处理\(\varphi(d)d^2\)的前缀和,可以加速很多。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=10000010;
ll read(){ll x;scanf("%lld",&x);return x;}
map<ll,ll>s;
int s0[N];
ll mod,inv4,inv6;
int quick(int a,ll b){int t=1;while(b){if(b&1)t=(ll)t*a%mod;b=b/2;a=(ll)a*a%mod;}return t;}
void init()
{
int v[N],phi[N],pri[N],m=0;
memset(v,0,sizeof(v));
phi[0]=0;
phi[1]=s0[1]=1;
for(int i=2;i<=10000000;i++)
{
if(v[i]==0)
{
v[i]=i;
pri[++m]=i;
phi[i]=i-1;
}
for(int j=1;j<=m;j++)
{
if(pri[j]>v[i]||pri[j]>10000000/i)
break;
v[i*pri[j]]=pri[j];
if(i%pri[j]==0)
phi[i*pri[j]]=phi[i]*pri[j];
else
phi[i*pri[j]]=phi[i]*(pri[j]-1);
}
s0[i]=(s0[i-1]+1ll*phi[i]*i%mod*i)%mod;
}
}
ll ask3(ll n)//求i^3的前缀和
{
n=n%mod;
return (n*n%mod*n%mod*n+n*n%mod*n%mod*2+n*n)%mod*inv4%mod;
}
ll ask2(ll n)
{
n=n%mod;
return n*(n+1)%mod*(2*n+1)%mod*inv6%mod;
}
ll S(ll l,ll r);
ll S(ll n)//求phi(d)*d^2的前缀和
{
if(n<=10000000)
return s0[n];
if(s.count(n))
return s[n];
ll sum=0;
sum=ask3(n);
for(ll l=2,r;l<=n;l=r+1)
{
r=n/(n/l);
sum=(sum-(ask2(r)-ask2(l-1))*S(n/l))%mod;
}
return s[n]=sum;
}
ll S(ll l,ll r)//求phi(d)d^2的区间和
{
return (S(r)-S(l-1))%mod;
}
ll ask(ll n)
{
ll ans=0;
for(ll l=1,r;l<=n;l=r+1)
{
r=n/(n/l);
ll t=n/l;
t=t%mod;
ans=(ans+S(l,r)*ask3(t))%mod;
}
return (ans+mod)%mod;
}
int main()
{
mod=read();
init();
inv4=quick(4,mod-2);
inv6=quick(6,mod-2);
cout<<ask(read());
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号