wqs二分
先讲一个问题
对于给定的,斜率单调的函数f(x)和一个k,请问y=kx+b和f(x)的切点下标
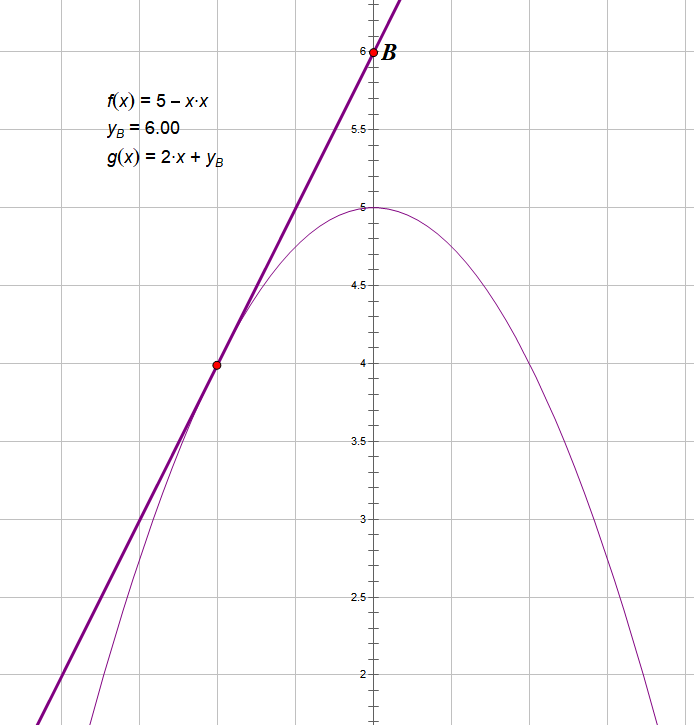
由于f(x)斜率单调,我们可以二分横坐标,计算f(x)的斜率,与k进行比较来看二分怎么调整
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=200010,mod=998244353;//1e9+7;
ll read(){ll x;scanf("%lld",&x);return x;}
ll quick(ll a,ll b){ll t=1;while(b){if(b&1)t=t*a%mod;b=b/2;a=a*a%mod;}return t;}
int lowbit(int x){return x&(-x);}
const double eps=1e-6;
double f(double x)//计算x位置的函数值
{
return 5-x*x;
}
double df(double x)//计算x位置的斜率
{
return (f(x+eps)-f(x))/eps;
}
double ask(double k)//询问斜率为k的切点横坐标
{
double l=-1e9,r=1e9,mid;
for(int i=1;i<=1000;i++)
{
mid=(l+r)/2;
if(df(mid)>=k)
l=mid;
else
r=mid;
}
return l;
}
int main(){
cout<<ask(2);
}
注意到(x,F(x))就表示恰好选x的时候切点的下标
P2619
设f(x)表示恰好选x个白边的最小生成树的权值和,则(x,f(x))呈现一个凹函数。
我们现在任选一个k,给每条白边减k,求最小生成树,发现有x个白边,最小生成树的花费为b,这个b表示什么呢。发现他就是\(f(x)-k*x\),也就是过\((x,f(x))\)的直线\(f'(x)*x+b=0\)的截距b
为什么要减而不是加k?因为减k时小k对应小x,大k对应大x,和我们的切线图更加匹配,二分起来更自然
知道这一点后,我们二分k,能顺便求x和f(x),当x=need的时候,b+k*x就是f(x)
但是如果二分终点l+1=r这里发现-l的时候x小于need,-r的时候x大于need,那岂不是很尴尬
因为题目保证有解,出现这种情况是因为存在白边边权=黑边边权,我们将一些白边换成黑边即可,也就是当点数大于等于need的时候都认为正确,计算答案
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010;
int lowbit(int x){return x&(-x);}
ll read(){ll x;scanf("%lld",&x);return x;}
int n,m,need,fa[N];
int sum;
struct edge
{
int c,x,y,col;
friend bool operator <(edge a,edge b)
{
return a.c==b.c?a.col<b.col:a.c<b.c;//如果c相同就让col为0的放前面
}
};
vector<edge>e[2],ee;
int get(int x)
{
return fa[x]==x?x:fa[x]=get(fa[x]);
}
int check(int k)
{
int num=0;
for(int i=1;i<=n;i++)
fa[i]=i;
sum=0;
ee=e[1];
for(auto [c,x,y,col]:e[0])
{
ee.push_back({c-k,x,y});
}
sort(ee.begin(),ee.end());
for(auto [c,x,y,col]:ee)
{
if(get(x)==get(y))
continue;
num+=(col==0);
sum+=c;
fa[fa[x]]=fa[y];
}
return num;
}
int main()
{
n=read();m=read();
need=read();
for(int i=1;i<=m;i++)
{
int x=read()+1,y=read()+1,c=read(),col=read();
e[col].push_back({c,x,y,col});
}
int l=-110,r=110,mid,ans;
while(l+1<r)
{
mid=(l+r)/2;
if(check(mid)>=need)
r=mid;
else
l=mid;
}
if(check(l)>=need)
ans=sum+need*l;
else if(check(r)>=need)
ans=sum+need*r;
else
ans=-1;
cout<<ans;
}
AT_abc400_G
如果随便拿怎么dp出最大值
\(f[i][j][k][l]\)表示1~i拿的最大值,当前有j(0/1)个ai没配对,k(0/1)个bi没配对,l(0/1)个ci没配对
dp的时候用pair表示最大值和拿取的数量
随便拿的时候,他必定会拿\({\lfloor {n\over 2}\rfloor}*2\)个
我们继续画(x,f(x))表示恰好拿x个的最大收益,可以想象到\(f'(x)\)是单调减的,因为\(f'(x)\)含义是增加1个选取对数,能多获得多少收益,因此刚开始收益很大,越往后可选范围越小,能获得的收益越小
给每个ai,bi,ci都+k,拿到一个最大收益b和对应的对数x,这个b就是f(x)+2kx,并且k越大x越大,k越小x越小,便于二分
对于二分终点,如果l位置拿的小于2k,r位置拿的大于2k,我的代码是找l位置,也就是小于等于2k的最大位置
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010;
int lowbit(int x){return x&(-x);}
ll read(){ll x;scanf("%lld",&x);return x;}
pair<ll,int> operator + (pair<ll,int>a,pair<ll,int>b)
{
a.first+=b.first;
a.second+=b.second;
return a;
}
pair<ll,int>max(pair<ll,int>a,pair<ll,int>b)
{
if(a.first>b.first)
return a;
else if(a.first<b.first)
return b;
else
{
if(a.second>b.second)
return b;
else
return a;
}
}
ll n,a[N],b[N],c[N];
pair<ll,int>f[N][2][2][2];
pair<ll,int>check(int v)
{
for(int i=1;i<8;i++)
f[0][i&1][i>>1&1][i>>2&1]={-1e16,0};
for(int i=1;i<=n;i++)
for(int j=0;j<=1;j++)
for(int k=0;k<=1;k++)
for(int l=0;l<=1;l++)
{
f[i][j][k][l]=f[i-1][j][k][l];
f[i][j][k][l]=max(f[i][j][k][l],f[i-1][j^1][k][l]+make_pair(2*a[i]+v,1));
f[i][j][k][l]=max(f[i][j][k][l],f[i-1][j][k^1][l]+make_pair(2*b[i]+v,1));
f[i][j][k][l]=max(f[i][j][k][l],f[i-1][j][k][l^1]+make_pair(2*c[i]+v,1));
}
return f[n][0][0][0];
}
void print(int x,int k)
{
auto t=check(x);
cout<<(t.first-2ll*x*k)/2<<'\n';
}
void work()
{
n=read();
int k=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
b[i]=read();
c[i]=read();
}
ll l=-2e9,r=0,mid;
while(l+1<r)
{
mid=(l+r)/2;
auto t=check(mid);
if(t.second<=k*2)
l=mid;
else
r=mid;
}
if(check(r).second<=k*2)
print(r,k);
else if(check(l).second<=k*2)
print(l,k);
}
int main()
{
for(int t=read();t;t--)
work();
}
洛谷P4983
首先这个式子,可以使用把\(\overline x\)提出来,或者暴力去括号约分再回括号的方式,得到他其实是\(((\sum a[i])+1)^2\)
如果没有m的限制,我们可以先来一个\(P(n^2)\)的dp
\(f[i]=min(f[j]+(sum[i]-sum[j]+1)*(sum[i]-sum[j]+1))\)
暴力去括号,和j无关的拿到外面,ij有关的还放在里面,可以得到一个便于斜率优化的式子
\(f[i]=sum[i]^2+2*sum[i]+1+min(f[j]-2*sum[j]+sum[j]^2-2*sum[i]*sum[j])\)
sum[i]在单调增,f[i]也在单调增
设\(F[i]\)表示\(f[j]-2*sum[j]+sum[j]^2\)
把\((2*sum[j],F[i])\)看成平面上的点,\(F[j]-sum[i]*2*sum[j]\)是某个斜率的最小截距,因此需要维护下凸包
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010;
int lowbit(int x){return x&(-x);}
ll read(){ll x;scanf("%lld",&x);return x;}
int n,m;
ll a[N],sum[N],f[N];
struct node{ll x,f;};
vector<node>q;
int ask(node a,node b,node c)
{
return 1.0*(c.f-b.f)/(c.x-b.x)<=1.0*(b.f-a.f)/(b.x-a.x);
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
sum[i]=sum[i-1]+a[i];
}
int now=0;
q.push_back({0,0});
for(int i=1;i<=n;i++)
{
while(now+1<q.size()&&q[now].f-sum[i]*q[now].x>q[now+1].f-sum[i]*q[now+1].x)
now++;
f[i]=q[now].f-sum[i]*q[now].x+sum[i]*sum[i]+2*sum[i]+1;
while(q.size()>=2&&ask(q[q.size()-2],q[q.size()-1],{2*sum[i],f[i]-2*sum[i]+sum[i]*sum[i]}))
q.pop_back();
q.push_back({2*sum[i],f[i]-2*sum[i]+sum[i]*sum[i]});
now=min(now,(int)q.size()-1);
}
cout<<f[n];
}
我们开始考虑wqs二分:
如果ai都大于0,他每个小的自成一段比较好。如果有小于等于0的则合成一段更优秀,比如0000或者-1 -2 2 3
不妨设最优解的分段数量为len,则强制分为m段,当m小于len,收益大于分为len段,当m大于len,收益也会变大,这是一个凹函数
怎么证明斜率单调?
好像只能意会一下
不管了,开始wqs二分
给每一段的贡献额外-mid,则大mid对应大段数,小mid对应小段数,便于二分
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010;
int lowbit(int x){return x&(-x);}
ll read(){ll x;scanf("%lld",&x);return x;}
int n,m;
ll a[N],sum[N];
pair<ll,int>f[N];
struct node{ll x,f,cnt;};//存横坐标,纵坐标,数量cnt
int ask(node a,node b,node c)
{
return 1.0*(c.f-b.f)/(c.x-b.x)<=1.0*(b.f-a.f)/(b.x-a.x);
}
pair<ll,int>check(ll v)
{
vector<node>q;
int now=0;
q.push_back({0,0,0});
for(int i=1;i<=n;i++)
{
while(now+1<q.size()&&q[now].f-sum[i]*q[now].x>q[now+1].f-sum[i]*q[now+1].x)
now++;
f[i].first=q[now].f-sum[i]*q[now].x+sum[i]*sum[i]+2*sum[i]+1-v;
f[i].second=q[now].cnt+1;
while(q.size()>=2&&ask(q[q.size()-2],q[q.size()-1],{2*sum[i],f[i].first-2*sum[i]+sum[i]*sum[i]}))
q.pop_back();
q.push_back({2*sum[i],f[i].first-2*sum[i]+sum[i]*sum[i],f[i].second});
now=min(now,(int)q.size()-1);
}
return f[n];
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
sum[i]=sum[i-1]+a[i];
}
ll l=-1e16,r=0,mid;
while(l+1<r)
{
mid=(l+r)/2;
if(check(mid).second<m)
l=mid;
else
r=mid;
}
if(check(l).second<=m)
cout<<f[n].first+l*m;
else
{
check(r);
cout<<f[n].first+r*m;
}
}
洛谷P5633
让s的连边恰好连k个
考虑最优解练了x个
给s的连边-mid再跑最小生成树,则大mid对应大k,小mid对应小k,便于二分
将s有关的边单独存储并排序,-mid后可以不sort,而是归并两个有序数组,复杂度更低
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=200010,mod=998244353;//1e9+7;
ll read(){ll x;scanf("%lld",&x);return x;}
ll quick(ll a,ll b){ll t=1;while(b){if(b&1)t=t*a%mod;b=b/2;a=a*a%mod;}return t;}
int lowbit(int x){return x&(-x);}
int n,m,s,k,fa[N];
struct edge
{
int x,y,v;
friend bool operator <(edge a,edge b)
{
return a.v<b.v;
}
};
vector<edge>e,ee,t;
void merge(int v)
{
t.clear();
int i=0,j=0,siz1=e.size(),siz2=ee.size();
while(i<siz1||j<siz2)
{
if(i<siz1&&j<siz2)
{
if(ee[j].v-v<=e[i].v){
t.push_back({ee[j].x,ee[j].y,ee[j].v-v});
j++;
}
else
{
t.push_back(e[i]);
i++;
}
}
else if(i<siz1)
{
t.push_back(e[i]);
i++;
}
else
{
t.push_back({ee[j].x,ee[j].y,ee[j].v-v});
j++;
}
}
}
int get(int x)
{
return fa[x]==x?x:fa[x]=get(fa[x]);
}
pair<ll,int>ask(int v)
{
for(int i=1;i<=n;i++)
fa[i]=i;
merge(v);
int cnt=0;
ll sum=0;
for(int i=0;i<m;i++)
{
if(get(t[i].x)!=get(t[i].y))
{
fa[fa[t[i].x]]=fa[t[i].y];
sum+=t[i].v;
if(t[i].x==s)
cnt++;
}
}
return {sum,cnt};
}
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
n=read();
m=read();
s=read();k=read();
for(int i=1;i<=m;i++)
{
int x=read(),y=read(),v=read();
if(y==s)
swap(x,y);//规定s排前面
if(x==s)
ee.push_back({x,y,v});
else
e.push_back({x,y,v});
}
sort(e.begin(),e.end());
sort(ee.begin(),ee.end());
int l=-4e4,r=4e4,mid;
if(ask(l).second>k||ask(r).second<k)
{
cout<<"Impossible";
return 0;
}
while(l+1<r)
{
mid=(l+r)/2;//大于等于的第一个位置
if(ask(mid).second<k)
l=mid;
else
r=mid;
}
if(ask(l).second>=k)
cout<<ask(l).first+k*l;
else
cout<<ask(r).first+k*r;
}
CF125E
是上一题的加强版
基本代码还不变,输出方案看起来只需要来一个flag记录有没有用这条边,来一个i记录原始下标就好了
实际上会wa9,因为你选的边数很有可能大于k,这个时候是不合法的
我们再跑一次,当数量等于k之后就不用s相关的边即可。相当于用非s相关的边替换掉了多选了的s相关的边
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=200010,mod=998244353;//1e9+7;
ll read(){ll x;scanf("%lld",&x);return x;}
ll quick(ll a,ll b){ll t=1;while(b){if(b&1)t=t*a%mod;b=b/2;a=a*a%mod;}return t;}
int lowbit(int x){return x&(-x);}
int n,m,k,fa[N];
struct edge
{
int x,y,v,i,flag;
friend bool operator <(edge a,edge b)
{
return a.v<b.v;
}
};
vector<edge>e,ee,t;
void merge(int v)
{
t.clear();
int i=0,j=0,siz1=e.size(),siz2=ee.size();
while(i<siz1||j<siz2)
{
if(i<siz1&&j<siz2)
{
if(ee[j].v-v<=e[i].v){
t.push_back({ee[j].x,ee[j].y,ee[j].v-v,ee[j].i,ee[j].flag});
j++;
}
else
{
t.push_back(e[i]);
i++;
}
}
else if(i<siz1)
{
t.push_back(e[i]);
i++;
}
else
{
t.push_back({ee[j].x,ee[j].y,ee[j].v-v,ee[j].i,ee[j].flag});
j++;
}
}
}
int get(int x)
{
return fa[x]==x?x:fa[x]=get(fa[x]);
}
pair<ll,int>ask(int v)
{
for(int i=1;i<=n;i++)
fa[i]=i;
merge(v);
int cnt=0;
ll sum=0;
for(int i=0;i<m;i++)
{
if(get(t[i].x)!=get(t[i].y))
{
fa[fa[t[i].x]]=fa[t[i].y];
sum+=t[i].v;
if(t[i].x==1)
cnt++;
t[i].flag=1;
}
else
t[i].flag=0;
}
return {sum,cnt};
}
void print(int v)
{
for(int i=1;i<=n;i++)
fa[i]=i;
merge(v);
int cnt=0;
ll sum=0;
for(int i=0;i<m;i++)
{
t[i].flag=0;
if(cnt==k&&t[i].x==1)
continue;
if(get(t[i].x)!=get(t[i].y))
{
fa[fa[t[i].x]]=fa[t[i].y];
sum+=t[i].v;
if(t[i].x==1)
cnt++;
t[i].flag=1;
}
}
cout<<n-1<<'\n';
for(int i=0;i<m;i++)
if(t[i].flag)
cout<<t[i].i<<' ';
}
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
n=read();
m=read();
k=read();
for(int i=1;i<=m;i++)
{
int x=read(),y=read(),v=read();
if(y==1)
swap(x,y);//规定s排前面
if(x==1)
ee.push_back({x,y,v,i});
else
e.push_back({x,y,v,i});
}
sort(e.begin(),e.end());
sort(ee.begin(),ee.end());
int l=-1e5,r=1e5,mid;
if(ask(l).second>k||ask(r).second<k)
{
cout<<"-1";
return 0;
}
while(l+1<r)
{
mid=(l+r)/2;//大于等于的第一个位置
if(ask(mid).second<k)
l=mid;
else
r=mid;
}
if(ask(l).second>=k)
print(l);
else
ask(r),print(r);
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号