2025.11 做题记录
P3412 仓鼠找sugar II
solution
先把题意转化成,求对于所有 \(a,b\) 的情况,从 \(a\) 走到 \(b\) 的期望步数和。
对于这个东西,把每条边的贡献拆出来。答案即 \(\sum 每条边的经过次数 \times 走过每条边的期望步数\)。
下文 \(siz_u\) 为 \(u\) 的子树大小,\(deg_u\) 为 \(u\) 的度数,\(v\in u\) 表示 \(v\) 是 \(u\) 的儿子,\(fa\) 默认 \(u\) 的父亲。
设 \(f_u\) 为从 \(u\) 走到 \(fa\) 的期望步数,\(g_u\) 为从 \(fa\) 走到 \(u\) 的期望步数。
我们有:
求这个东西没什么难度吧!
然后计算每条边的经过次数。其实比较简单,\(u\) 走到 \(fa\) 的话可选择的起点个数为 \(siz_u\),终点个数为 \(n-siz_u\)。\(fa\) 走到 \(u\) 同理。
直接统计答案即可。
P3527 [POI 2011] MET-Meteors
在这题 mark 一下整体二分。
solution
考虑只有一个国家怎么做。扫过去当然是可以的。
使用二分。判断一个 \(i\) 合不合法时,将 \([1,i]\) 的修改全部做完,如果修改后的陨石数量 \(\ge\) 需求量说明答案 \(\le i\)。复杂度 \(O(n\log n)\)。
那么 \(n\) 个国家呢?直接做显然就爆了。但是我们发现做了很多冗余的操作。比如说,第一轮 \(\operatorname{check}(\frac{n}{2})\) 时,所有的国家都会把 \([1,\frac{n}{2}]\) 的操作全部做一次。
所以可以把一些答案确定的区间相同的询问合并在一起做。这样说有点抽象,具体来说:
\(\operatorname{dvd}(L,R,l,r)\) 表示需要处理国家(编号)在 \([L,R]\) 范围内,它们目前的答案范围均为 \([l,r]\)。
我们将 \([1,mid]\) 的操作全部做完(不止一个国家,所以需要上数据结构。BIT 即可。)。此时扫一遍,判断哪些国家已经收集到足够陨石了,将它们扔进 \([l,mid]\) 中,否则扔进 \([mid+1,r]\) 中。实现时可以将合法的部分重新放在 \([L,L+cnt-1]\) 中,剩下的往后排。就不需要用什么动态数组了!
复杂度 \(O(n\log^2 n)\)。
code
当然不能真的“将 \([1,mid]\) 的操作全部做完”。有两种处理方式:
- 做完当前区间先递归进入右区间,不删除贡献(类似莫队写法?)。这个比较好写,但是在有默认时间维时显然会出问题。
- 把要递归进右区间的询问 \(k\) 减去 \([1,mid]\) 部分的贡献。
其实感觉说得还是一坨。代码比较好理解。
扔一个分治部分的实现方式。
void dvd(int L,int R,int l,int r){
if(L>R||l>r) return;
if(l==r){for(int i=L;i<=R;i++) ans[p[i]]=l;return;}
const int mid=(l+r>>1);
while(liz<mid) upda(++liz,1);while(liz>mid) upda(liz--,0);
int lx=0,ly=0;
for(int i=L;i<=R;i++){chk(p[i])?(x[++lx]=p[i]):(y[++ly]=p[i]);}
for(int i=1;i<=lx;i++) p[L+i-1]=x[i];
for(int i=1;i<=ly;i++) p[R-i+1]=y[i];
dvd(R-ly+1,R,mid+1,r);dvd(L,L+lx-1,l,mid);
}
P3332 [ZJOI2013] K大数查询
solution
二分答案,线段树(因为我不会树状数组维护区间加区间查)维护一段区间内的集合 \(\ge mid\) 的数总共有多少个。
注意这题就属于上文提到的“有默认时间维”一类。
code
因为要保证相对顺序(时间维)稳定,所以略繁琐一点?
void dvd(int L,int R,int l,int r){
if(L>R||l>r) return;
if(l==r){for(int i=L;i<=R;i++) ans[p[i]]=l;return;}
const int md=(l+r>>1);
int lx=0,ly=0;
for(int z=L,i;z<=R;z++){
i=p[z];
if(!o[i].op){
if(o[i].x>md){y[++ly]=i;upda(i,1);}
else{x[++lx]=i;}
}
else{chk(i)?(y[++ly]=i):(x[++lx]=i);}
}
for(int i=1;i<=ly;i++){if(!o[y[i]].op) upda(y[i],-1);}
for(int i=1;i<=lx;i++) p[L+i-1]=x[i];
for(int i=1;i<=ly;i++) p[L+lx+i-1]=y[i];
dvd(L,L+lx-1,l,md);dvd(R-ly+1,R,md+1,r);
}
P1527 [国家集训队] 矩阵乘法
solution
mark 二维树状数组。
其余没区别了。
code
P2617 Dynamic Rankings
solution
把更改一个点的值拆成在删除一个值后加入一个值。
code
P3250 [HNOI2016] 网络
solution
先想想单个询问二分怎么做。
判断所有 \(w>mid\) 的路径是否都经过了 \(u\)。如果都经过了说明答案 \(\le mid\),反之亦然。
可以记录有多少条 \(w>mid\) 的路径,然后对于每条这样的边,给边上的所有点打标记。判断一个点上的标记个数是否等于总数即可。
给路径打标记是经典 trick。即给根分别到 \(u,v\) 的路径 \(+1\),根到 \(lca,fa_{lca}\) 的路径上 \(-1\),单点查询。等价于单点修这几个点,查询子树和。dfn 序 + BIT 简单维护。
然后搬到整体二分的板子上就做完了!
code
P3242 [HNOI2015] 接水果
solution
设 \(l_u=dfn_u,r_u=dfn_u+siz_u-1\)。
考虑一条路径 \((x,y)\) 包含 \((u,v)\) 时 \((x,y)\) 和 \((u,v)\) 的关系。比较复杂就不列了(懒!)。
最后一定形如 \(l_x\in [],l_y\in[]\)。即平面上的一个点 \((x,y)\) 在一个矩形内。
那么我们给每个矩形打标记,即可快速统计 \((x,y)\) 包含了多少条路径。
还是先想单个二分怎么做。把每个 \(w\le mid\) 的盘子打上标记,统计 \((x,y)\) 包含的盘子个数是否 \(\ge k\)。如果是说明答案 \(\le mid\),反之亦然。
套上整体二分即可。注意这个没有默认时间维,但是扫描线时需要保证 \(y\) 是单调不降的。把 \(y\) 当作默认时间维即可。
code
难吃。
模拟赛 姨(aunt)
我不会数学。。
solution
设 \(N\) 为 \(n^2\), \(f_i\) 为恰好选 \(i\) 个的方案数,\(g_i\) 为钦定选 \(i\) 个的方案数(题目要求是二维,但这不重要)。
我们有:\(f_i=\sum_{j\ge i}(-1)^{j-i}\binom{j}{i}g_j\)。
把期望转成总数除以方案数,总方案数显然为 \(A_m^N\binom{k}{m}\),最后除掉即可。题目所求为:
于是转化为求所有 \(g_{i,j}\)。
其中 \(x=n\times i+n\times j-i\times j\),即钦定染黑的格子数量。
上式的每一项意义分别为:随便填数在方格中的方案数,选择行数的情况数,选择列数的情况数,除了钦定需要染黑的格子外剩下选出染黑的数字的情况数。最后一项不是 \(\binom{m}{k}\) 的原因是,我们已经给所有格子填入数字,并且钦定其中的 \(x\) 个必须染黑,也就是那 \(x\) 个格子填入的数字必须选在 \(k\) 个数字中。于是剩下可以选择的染黑数字个数为 \(k-x\),可以选择的数字个数为 \(m-x\)。
于是答案为:
P3350 [ZJOI2016] 旅行者
平面图最短路模板题。
solution
考虑分治,把一张图从中间劈开。在分治范围外的询问和分治后两边内部的最短路就不需要考虑了,也就是说仅仅需要考虑经过劈开那条线的最短路,如下图。
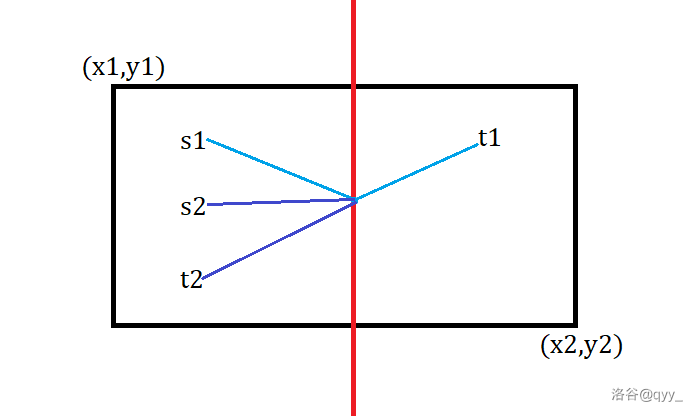
预处理出红线上每个点到两边所有点的最短路。询问就被分为类似图中两种情况。每次用 \(dis(u,s)+dis(u,t)\) 更新答案即可。
每次红线选在当前分支区间的长边的中点上。显然这样最优。
设 \(N=nm\),这样做的复杂度是 \(O(N\sqrt N \log N+Q\sqrt N)\),我不会证明。每次都选横 / 竖边复杂度就错了。
code
感觉跟整体二分没啥区别!除了长没有难写的点。
CF232E Quick Tortoise
solution
大体方向跟上题差不多。但是直接做的话会 T。
枚举中线上的点,设 \(f_{i,j}\) 为 \((i,j)\) 能否到达当前点,\(g_{i,j}\) 为当前点能否到达 \((i,j)\)。
显然有转移:\(f_{i,j}\gets f_{i+1,j}\or f_{i,j+1}\),\(g_{i,j}\gets g_{i-1,j}\or g_{i,j-1}\)。
对于每一个枚举的点来说,转移的过程毫无区别,并且求的只是可达性。所以 bitset 优化做完!
code
P6116 [JOI 2019 Final] 有趣的家庭菜园 3 / Growing Vegetables is Fun 3
归来还是不会蓝!
solution
有显然的性质:每种颜色的植物相对顺序不会改变。
设 \(dp_{i,j,k,0/1/2}\) 表示当前放到第 \(i\) 个位置,已经放了 \(j\) 个 \(0\),\(k\) 个 \(1\),(\(i-j-k\) 个 \(2\),)当前放 \(0/1/2\) 的最小代价。由上面的性质,当前所需要放的植物一定是确定的。
这个东西转移的代价显然和“所需要植物的当前位置”相关。当前位置即进行了前面操作后这盆植物的位置。想想怎么计算。
假设当前需要的颜色是 \(0\),这盆植物原编号是 \(p\),现编号是 \(w\)。那么如果 \([1,p]\) 中 \(1\) 的个数 \(cnt_1\) \(<k\)(\(2\) 同理,不赘述),显然 \(w\) 比 \(p\) (被)往后多交换了 \(k-cnt_1\) 次。于是有:\(w=p+\max(0,k-cnt_1)+max(0,i-j-k-cnt_2)\)。
\(p,cnt\) 预处理都是好求的。
于是做到 \(O(n^3)\)。
流浪者的背包(knapsack)
属于 下次见到不可能会 题。
solution
考虑二进制拆分,然后当成 01 背包来做。
设 \(dp_{i,j}\) 表示考虑了前 \(i\) 位,当前位为 \(j\)(即不考虑二进制,后面进的位和当前位放的数之和)。
转移(这里的 \(a_k\) 即相当于 \(2^i a_k\)):
- \(dp_{i,j}\gets dp_{i,j-a_k}\)
- \(dp_{i+1,\frac{j}{2}}\gets dp_{i,j},j\equiv m 的第 i 位 \pmod 2\)
比较好理解吧。
于是做到复杂度 \(O(nV\log m)\),其中 \(V\) 是 \(\max j\),不难分析出最大值为 \(O(\sum a)\),可以通过。
P6976 [NEERC 2015] Distance on Triangulation
solution
因为给出的图是一个三角剖分,所以当我们拉出一条边以它为分界线,一定可以把这张图分为点集(除了这条边本身)互相独立的两部分。相当于两个独立子问题。
于是考虑分治。\(dvd(Q,P,E)\) 表示当前分治到的询问集合为 \(Q\),点集为 \(P\),边集为 \(E\)。
选出一条边后,这张图上询问的答案被分为了“经过这条边的端点”和“不经过这条边端点”两种情况。
“经过”的部分显然可以直接从该边的两端点进行 bfs,求出答案。“不经过”在子问题中考虑。
显然,选择的边应该是分出两个点集大小较大值最小的一条边。因为这是一个按顺序编号的多边形,所以算这条边两边分别有几个点也是容易的。具体来说,假设选的边为 \((u,v)\)(\(u< v\)),那么两个点集的编号范围分别为 \([1,u] \vee [v,n]\),\([u,v]\)。可以做到 \(O(1)\) 计算当前点集分别有几个点落在这两个范围内。
复杂度 \(O(n\log n)\)。
注意,分出的这两个集合必须包含 \(u,v\) 本身。
:::info[感性理解]
否则不能保证分出的点集是连通图。这样显然有问题,因为在不连通图中,不一定能找到一条边,使得两个点集较大值不超过原来的一半(即子问题规模并没有减半),时间复杂度无法得到保障。
:::
code
P3206 [HNOI2010] 城市建设
动态最小生成树!其实我觉得不能算是 cdq 分治。
solution
考虑对于询问分治,假设当前分治到的区间是 \([l,r]\)。
我们称 \([l,r]\) 内涉及的边为“动态边”,其余为“静态边”。暴力做的问题就是“静态边”太多了,每次都处理一遍会爆炸。
思考怎么删掉一些“静态边”。
- 对于所有“静态边”跑一遍最小生成树。这时,不在生成树内的“静态边”一定是无用的,全部丢掉。
- 在生成树中强制加入所有“动态边”,再对于“静态边”跑一遍最小生成树。此时仍然在生成树中的“静态边”最后一定在最小生成树中,所以将其在当前层提前加入,不需要再考虑。
假设区间长度为 \(len\)。那么显然,对于一层来说,它需要处理的静态边是 \(O(len)\) 的。
终止条件即 \(l=r\)。先判断原图是否已经是最小生成树,如果不是,决策一下用哪条边即可。
复杂度 \(O(n \log^2 n)\)。
code
需要使用可撤销并查集维护连通性。
先递归左区间,就不需要额外更新 / 还原边权了。
P4719 【模板】动态 DP
没有咋想到的部分。模板题就模板题吧。
solution
朴素做法不记。优化考虑树剖。
设 \(g_{i,0/1}\) 表示只考虑 \(i\) 的子树且不考虑 \(i\) 的重儿子的子树,选 / 不选 \(i\) 的答案,\(f_{i,0/1}\) 为考虑 \(i\) 的重儿子的答案。
设 \(p=son_i\)。
转移分别为:
设 \(F_i,G_i\):
定义矩乘运算为 \((\max,+)\)。我们有:\(F_i=G_i* F_p\)。
关于为什么这么构造,因为我们需要使得跟 \(i\) 无关的一项继续分裂,也就不能让带 \(f\) 的项成为“转移”的矩阵。
于是显然只需要知道 \(F_1\)。不难发现 \(F_1=\prod_{top_v=1} G_v\)。所以这个 \(F\) 其实不需要真的维护,每次需要的时候拉出来求就好了。这个线段树随便维护吧!
考虑修改会影响哪些节点。首先当前点的 \(G\) 一定会被更新。进而当前点这条链上的 \(F\) 都会被更新。当前链头一定不是它父亲的重儿子,所以它父亲的 \(G\) 一定会被更新,以此往复。所以说每次需要更改的 \(G\) 是即需要跳的链条数。
用线段树维护区间 \(G\) 的乘积。
复杂度 \(O(n\log^2 n)\)。
code
第一次写的时候 build 的时候忘记 pushu 了。
模拟赛 集合(set)
唐。
solution
不容易发现最终选出来的集合是一个公差为奇数的等差数列。
设 \(f_i\) 为最大值不超过为 \(i\) 且满足上述条件的数列个数,\(g_i\) 为 \(i\) 的奇数因子个数。
然后注意到并不是很在意等差序列具体的第一项大小。于是:\(f_i=2f_{i-1}-f_{i-2}+g_{i-1}\),其中 \(2f_{i-1}-f_{i-2}\) 是不同时选 \(1,i\) 的答案,\(g_{i-1}\) 是同时选 \(1,i\) 的答案(即公差种类数)。
我不会线性筛,所以复杂度 \(O(n\ln n)\)。
模拟赛 线路规划(route)
菜就多练。
solution
设传送门设在点 \(L,R\) 上。钦定 \(u\le v,L\le R\)。
外层显然先套一个二分答案 \(k\)。\(v_i-u_i\le k\) 的后面不用考虑。
要求就变为 \(\max (\lvert u_i-L\rvert+\lvert v_i-R\rvert)\le k\)。可以暴力分讨,但是我不会。
这个东西的形式就是曼哈顿距离。因为 \(\max\) 比较麻烦,所以经典结论转切比雪夫距离。
然后就变成了对于两维独立的不等式,判断是否有解。即求矩形是否有交。直接做即可。
复杂度 \(O(n\log n)\)。
模拟赛 橡子 6(acorn)
solution
钦定 \(L_u\le L_v\)。对于每条边的边权分讨:
- \(w<L_u\):没用。
- \(L_u\le w <L_v\):直接给 \(u\)。
- \(L_u+L_v\le w\):两边条件都可以直接满足。
- \(\text{otherwise}\):给 \(u\) 或者给 \(v\)。
只有第四种情况需要继续做,于是只保留这种情况的边。
对于保留下来的图,假设一个连通块剩余的未满足条件的点数是 \(d\),保留的边数是 \(e\)。那么这个连通块现在可以满足条件的点个数就是 \(\max(d,e)\)(因为至少是个树,容易证明通过调剂可以使得每条边都被用上)。
按上述模拟即可。
模拟赛 消消乐(game)
/kel。
solution
先缩一下点。按照颜色从小到大进行操作。假设当前颜色为 \(c\),长度为 \(l\),上一个颜色为 \(x\),下一个颜色为 \(y\)。显然,如果当前段可以被完全合并(\(l\equiv 0\pmod k\))成颜色为 \(x\)(或 \(y\),同理),直接把它并到 \(x\) 上(如果 \(x=y\) 那就三段并起来)。
否则,\(x\) 与 \(y\) 一定不能合成一段,也就是说当前段需要在 \(x,y\) 中选一个并(只有一边会成为最终答案)。但你不需要真的决策,因为两段已经独立了,可以分开加入然后直接把中间断开。
用链表模拟。复杂度 \(O(n)\)。
CF2143D2 Inversion Graph Coloring (Hard Version)
很有借鉴意义。
solution
简单转化:一个序列是“好”的当且仅当不存在长度 \(\ge 3\) 的严格下降子序列。
设 \(dp_{i,j,k}\) 为考虑了前 \(i\) 个数,最大值为 \(j\),长度为 \(2\) 的严格下降子序列中第二个数最大为 \(k\) 的方案数。
转移:
-
不选 \(a_i\):\(dp_{i-1,j,k}\to dp_{i,j,k}\)
-
选 \(a_i\),\(a_i\ge j\):\(dp_{i-1,j,k}\to dp_{i,a_i,k}\)
-
选 \(a_i\),\(j>a_i\ge k\):\(dp_{i-1,j,k}\to dp_{i,j,a_i}\)
第一维扔掉。观察一下,两个转移中有一维是不变的(可以枚举),另一维需要前缀求和,单点修改。注意到两维独立,所以对于两维分别开 \(n\) 个树状数组维护即可。
复杂度 \(O(n^2\log n)\)。
CF1887C Minimum Array
好题啊!
solution
注意到,区间加等价于单点修。
为什么呢?考虑以一开始的序列作为标准,区间加就在上面差分。然后惊人的发现!字典序的相对大小完全等价与差分数组的相对大小。
这个性质相当有用。在比较一开始的序列和任意序列时,只需要找到差分数组中第一个不为 \(0\) 的位置 \(p\),判断 \(b_p\) 与 \(0\) 的大小即可。
显然,我们不关系这个“一开始的序列”到底是不是一开始的序列。所以我们只要把它定义为目前的答案(序列),就可以 \(O(1)\) 判断它是否比现答案更优。
模拟这个过程咋做都行吧。可以用 set 维护不为 \(0\) 的位置,遇到一个新的答案就清空集合。复杂度 \(O(n\log n)\)。
code
模拟赛 原(gen)
没有会做构造题的义务!
solution
原本的操作太扭曲了,转化一下等价于可以把包含位置 \(i\) 的一段区间染色成 \(a_i\)。
于是可以把 \(b\) 中一段相同颜色的点给缩一下,缩点后每个位置对应 \(a\) 中的一个位置。显然能匹配尽量匹配的策略是不劣的。无解就是无法全部匹配。
考虑怎么构造方案。假设 \(a\) 中的位置 \(i\) 对应 \(b\) 中需要染的区间为 \([L_i,R_i]\)。
那么从左往右扫,依次把 \([L_i,i]\) 染成 \(a_i\)。同理,从右往左扫,依次把 \([i,R_i]\) 染成 \(a_i\)。这样一定是对的(不会存在染色前 \(a_i\) 被“污染”的情况),因为每对 \([L,R]\) 都是不交的,也就不会存在 \(i\) 被染成别的颜色后还需要往另一边染色的情况。显然每个位置最多被染色一次(只有在需要染色区间长度 \(\ge 2\) 的时候才有染色的必要),所以操作次数严格 \(\le n\)。
code
P7402 [COCI 2020/2021 #5] Sjeckanje
神仙。
solution
首先你需要惊人的注意力:一定存在一种最优划分使得划分出来的区间是单调的。感性理解就是,你在拐弯的地方把它劈开,答案不会更小。
然后看到区间加,使用差分。这与上面的结论惊人的契合:区间内原数组单调即差分数组正负性统一。
我们按照差分数组的正负性划分区间。那么一个区间的贡献即为:\(\sum |b_i|\)。
但是划分出来区间的交界处并不能同时取到。举个例子:
1 3 5 4 2
+2 +2/-1 -2
5 显然不能被前一段和后一段同时选,于是在 +2 和 -1 的贡献中只能选择一个。
思路非常明确了,合并区间考虑上线段树。
每个点维护 \(o_{0/1,0/1}\) 表示当前区间选不选左端点,选不选右端点的最大答案。
merge 时根据 \(b_{mid}\) 和 \(b_{mid+1}\) 的正负性进行合并。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号