2018.8.22 2018暑假集训之生日蛋糕

挑战一下NOI的题！！

---

题目背景

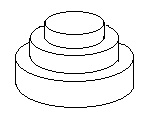
7月17日是Mr.W的生日，ACM-THU为此要制作一个体积为Nπ的M层

生日蛋糕，每层都是一个圆柱体。

设从下往上数第i(1<=i<=M)层蛋糕是半径为Ri, 高度为Hi的圆柱。当i<M时，要求 Ri>Ri+1R_i>R_{i+1}Ri​>Ri+1​ 且 Hi>Hi+1H_i>H_{i+1}Hi​>Hi+1​ 。

由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积Q最小。

令Q= Sπ

请编程对给出的N和M，找出蛋糕的制作方案（适当的Ri和Hi的值），使S最小。

（除Q外，以上所有数据皆为正整数）

题目描述

输入输出格式

输入格式：

有两行，第一行为N（N<=20000），表示待制作的蛋糕的体积为Nπ；第二行为M(M<=15)，表示蛋糕的层数为M。

输出格式：

仅一行，是一个正整数S（若无解则S=0）。

输入输出样例

输入样例#1：

100
2

输出样例#1：

68

明显dfs的题然而裸搜会TLE 经过计算大概需要三次剪枝才能过 
从各个方面考虑 
1、搜索顺序 本题明显倒着搜比正着搜快得多（可以为很多其他剪枝作铺垫）
2、可行性剪枝、最优解剪枝
在代码最开始对每层的最小体积与表面积进行初始化（由于上面比下面小所以第i层半径与高分别为i时体积与表面积最小）
这样可以派生出三种剪枝方法：
(1)看当前的体积加上剩余部分的最小体积是否超过要求体积 若超过则返回
(2)若当前表面积已经大于曾经求得的最小值则返回
(3)剩下体积除以最大(虽然取不到)半径所得到的表面积+累计表面积大于答案则退出
上AC代码

#include<iostream>
#include<cstdio>
#include<cmath>
#define f(i,a,b)    for(register int i=a;i<=b;++i)
#define fd(i,a,b)    for(register int i=a;i>=b;--i)
using namespace std;
const int N=20000+7;
int ans=987654321,n,m,Minv[N],Mins[N];
inline int read()//读入优化
{
      int num=0;
      char c;
      while(isspace(c=getchar()));
      while(num=num*10+c-48,isdigit(c=getchar()));
      return num;
}
bool flag=1;
inline void dfs(int now,int S,int V,int lasth,int lastr)
{
    if(now==0)//要是已经到了第一层就退出 
    {
        if(V==n)    ans=min(ans,S);//是否为合法答案 
        return;
    }
    //三重恶心的剪枝 
    if(S+2*(n-V)/lastr>ans)    return;
    //要是剩下体积除以最大(虽然取不到)半径所得到的表面积+累计表面积大于答案 退出 
    if(V+Minv[now]>n) return;//要是剩下来的体积已经小于该层最小体积了就退出 
    if(S+Mins[now]>ans)    return;//要是最小面积+当前累计表面积已经比已知答案大了就退出 
    fd(i,lastr-1,now)//从大到小枚举该层半径 
    {
        if(/*flag*/ now==m)    S=i*i;//要是现在是第一层那么就直接加上最小表面积 
    //    flag=0;
        int Maxh=min(lasth-1,(n-V-Minv[now-1])/(i*i));
        fd(j,Maxh,now)//从大到小枚举该层高度 
            dfs(now-1,S+2*i*j,V+i*i*j,j,i);
    }
}
int main()
{
    n=read();m=read();
    f(i,1,m)
        Minv[i]=Minv[i-1]+i*i*i,//cout<<Minv[i]<<endl,
        Mins[i]=Mins[i-1]+2*i*i;//cout<<Mins[i]<<endl;
    int MaxR=sqrt(n);
    dfs(m,0,0,n,MaxR);
    printf("%d",ans==987654321 ? 0 :ans);
    return 0;
}

感谢洛谷dalao@Liang_Shine_Sky帮助

---

在最后科普一下关于dfs优化及剪枝

1、搜索顺序优化

构建不同顺序下的搜索树，观察以什么顺序搜索时时间最短

2、可行性剪枝

应随时判断当前状态在剩余部分取最大/小极端时是否仍然无法达到结果，如果是则立即返回

3、等效冗余剪枝

对于完全对称的一些状态及子状态，应该确定一个方向进行搜索，可以大大减少搜索时间

4、最优解剪枝

若当前状态明显无法到达（同可行性剪枝）或已经超过目前求得的最优解，应立即返回

5、启发式优化

在搜索过程中加入保证正确的贪心策略（如调整循环范围及顺序等）进行优化

6、上下界剪枝

循环及递归过程中应尽量缩小上下界以确保时间在规定以内

7、原则

(1)正确：必须保证剪枝后的结果不会忽略正确答案

(2)准确：在剪枝的过程中，对范围的确定必须尽量准确，否则难以取得预期效果

(3)高效：剪枝本身由代码中的判断构成，但是尽管剪枝可以缩短时间，但是判断本身也消耗时间，必须尽量处理好这个矛盾