Tarjan

强连通分量

定义：一个有向图的最大强连通子图（子图中任意两点均可互相到达）

dfn(时间戳)：节点dfs遍历顺序

low：节点通过非返祖边能到达的最小dfn

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n,m,x,y,top,cnt,t,ans,aass;
//ans为强连通分量包含节点的最大数量,aass为强连通分量数量,n个节点,m条边
int head[N],dfn[N],stac[N],low[N];
bool vis[N];
struct edge{
	int v,next;
}e[1000020];
inline void add(int u,int v){ 
	e[++top] = (edge){v,head[u]};
	head[u] = top;
}
int read(){
	int x = 0,k = 1;
	char c = getchar();
	for(;!isdigit(c);c = getchar())if(c == '-')k = -1;
	for(;isdigit(c);c = getchar())x = (x<<1) + (x<<3) + c - '0';
	return x * k;
}
void tarjan(int now){
	dfn[now] = low[now] = ++cnt;
	stac[++t] = now;
	vis[now] = true;
	for(int i = head[now];~i;i = e[i].next)
		if(!dfn[e[i].v]){
			tarjan(e[i].v);
			low[now] = min(low[now],low[e[i].v]);
		}
		else if(vis[e[i].v])
			low[now] = min(low[now],dfn[e[i].v]);
	if(dfn[now] == low[now]){
		int cur,sum = 0;
		aass++;
		do{
			cur = stac[t--];
			vis[cur] = false;
			printf("%d ",cur);
			sum++;
		}while(now != cur);
		printf("\n");
		ans = max(ans,sum);
	}
}
int main(){
	n = read(),m = read();
	memset(head,-1,sizeof(head));
	for(int i = 1;i <= m;i++){
		x = read(),y = read();
		add(x,y);
	}
	for(int i = 1;i <= n;i++)
		if(!dfn[i])tarjan(i);
	printf("The max point(s) of Strongly Connected Component is : %d\n",ans);
	printf("The number of Strongly Connected Component(s) is(are) : %d",aass);
	return 0;
}

缩点

缩点就是把同一个强连通分量中的点染成同一种颜色，把图变成DAG

核心：

if(low[now] == dfn[now]){
		int cur,sum = 0;
		idx++;
		do {
			cur = stac[top--];
			vis[cur] = false;
			bel[cur] = idx;
			sum += point[cur];
//			for(int i = head[cur];~i;i = e[i].next)
//				dp[idx] = max(dp[idx],dp[bel[e[i].v]]);这两个语句是P3387的dp语句~
		} while(cur != now);
//		dp[idx] += sum;
//		ans = max(ans,dp[idx]);这两句也是
	}

其实再建一张新图也可以

割边（桥）

定义：删去这条边后无向图将不再连通

如果这条边的子节点无法通过非返祖边回到父节点，那么这条边就是割边

if(i == (lastedge ^ 1)) continue;
		if(!dfn[e[i].v]){
			tarjan(e[i].v,i);
			low[now] = min(low[now],low[e[i].v]);
			if(dfn[now] < low[e[i].v])
				p[++ans] = make_pair(min(now,e[i].v),max(now,e[i].v));
		}
		else low[now] = min(low[now],dfn[e[i].v]);

lastedge是返祖边，注意num从2开始

边双连通分量（边双）

就是一个两个点可以从多条不相交的路径互相到达的极大子图

和缩点一样，把同一个边双连通分量中的点染成同一种颜色就可以啦！

if(low[now] == dfn[now]){
		int cur;
		idx++;
		do {
			cur = stac[top--];
			bel[cur] = idx;
		} while(cur != now);
	}

洛谷P8436

void tarjan(int u,int last){
	dfn[u] = low[u] = ++cnt;
	stac[++top] = u;
	for(int i = head[u];i;i = e[i].next){
		if(i == (last ^ 1)) continue;
		if(!dfn[e[i].v]){
			tarjan(e[i].v,i);
			low[u] = min(low[u],low[e[i].v]);
		}
		else low[u] = min(low[u],dfn[e[i].v]);
	}
	if(low[u] == dfn[u]){
		int cur;
		idx++;
		do {
			cur = stac[top--];
			vec[idx].push_back(cur);
		} while(cur != u);
	}
}

割点、点双

割点定义：删去一个点以及其相邻的边后使得图不连通的点

一张没有割点的图为点双连通图，一张图中极大点双连通子图被称为点双连通分量，简称点双

一个 点双连通图 的一个定义是：图中任意两不同点之间都有至少两条点不重复的路径。

一个近乎等价的定义是：不存在割点的图。
这个定义只在图中只有两个点，一条连接它们的边时失效。它没有割点，但是并不能找到两条不相交的路径，因为只有一条路径。

性质：两个点双的交小于等于一。同时属于多个点双的点是割点

void tarjan(int now,int lastedge){
	dfn[now] = low[now] = ++cnt;
	stac[++top] = now;
	for(int i = head[now];~i;i = e[i].next){
		if(i == (lastedge ^ 1)) continue;
		if(!dfn[e[i].v]){
			tarjan(e[i].v,i);
			low[now] = min(low[now],low[e[i].v]);
			if(low[e[i].v] >= dfn[now]){
				idx++;
				deg[now]++;
				int cur;
				do{
					cur = stac[top--];
					deg[cur]++;
				}while(cur != e[i].v);
			}
		}
		else
			low[now] = min(low[now],dfn[e[i].v]);
	}
}//deg记录点的度数

带自环和孤立点的点双（洛谷P8435）

void tarjan(int u,int last){
	dfn[u] = low[u] = ++cnt;
	stac[++top] = u;
	bool flag = true,f2 = true;
	for(int i = head[u];i;i = e[i].next){
		flag = false;
		if(e[i].v != u) f2 = false;
		if(i == (last ^ 1)) continue;
		if(!dfn[e[i].v]){
			tarjan(e[i].v,i);
			low[u] = min(low[u],low[e[i].v]);
			if(low[e[i].v] >= dfn[u]){
				vec[++idx].push_back(u);
				int cur;
				do{
					cur = stac[top--];
					vec[idx].push_back(cur);
				}while(cur != e[i].v);
			}
		}
		else low[u] = min(low[u],dfn[e[i].v]);
	}
	if(flag || f2) vec[++idx].push_back(u);
}

2-SAT

SAT是Satisfiability（可满足性）问题的简写，k-SAT为m组要求，每组要求至少有一个满足即可（或运算），求合法方式。当k > 2时此问题是NP-完全的。

2-SAT为k = 2时的情况。

判断是否有合法方式

设某一组要求为x1 == true || x2 == false;

如果x1 == false可以推出x2 == false;同理，x2 == true可以推出x1 == true。（否则条件不成立）

建图，此时一个强连通分量内部的条件一定同时成立/不成立

如果一个变量的true和flase在同一个强连通分量里，那么无解。

重点：构造解

先传一张图：

x1 == false || x2 == true;

x1 == false || x2 == false;

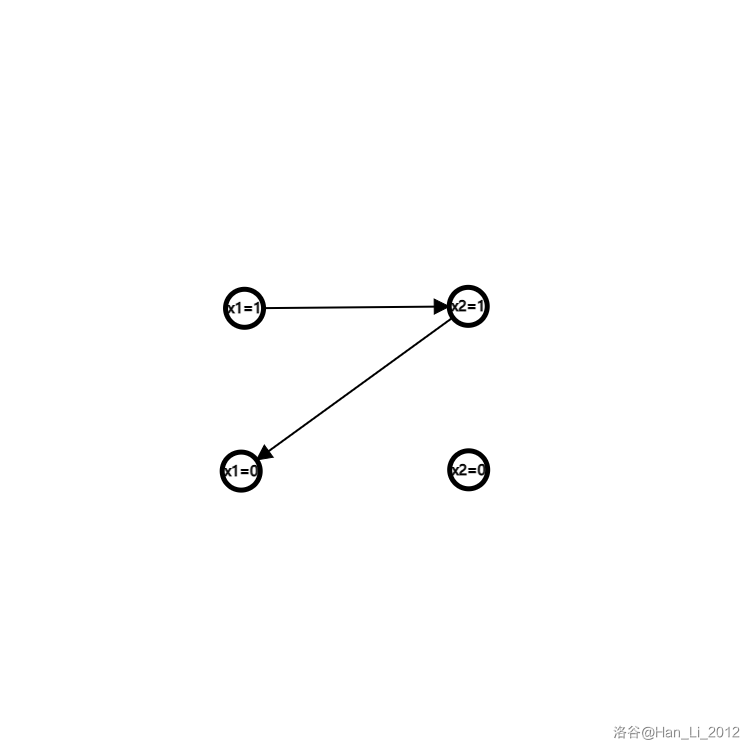
因为由x1 = true 可以推出 x1 = false，所以x1只能为false（后者不会推出前者）

所以给变量赋值优先用后遍历的值，由于tarjan是弹栈操作，后遍历的点被先弹出来作为一个强连通分量，故优先选bel（强连通分量编号）小的值赋值。

洛谷P4782代码（用i+n表示xi = false）

#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for(int i = 1;i <= n;i++)
#define repe(i,u) for(int i = head[u];i;i = e[i].next)
const int N = 2e6 + 5;
struct edge{
	int v,next;
}e[N];
int head[N],dfn[N],low[N],stac[N],bel[N],top,tot,idx,cnt,n,m,x1,x2,a,b;
bool vis[N];
inline void add(int u,int v){
	e[++tot] = (edge){v,head[u]};
	head[u] = tot;
}
void tarjan(int u){
	dfn[u] = low[u] = ++cnt;
	stac[++top] = u;
	vis[u] = true;
	repe(i,u)
		if(!dfn[e[i].v]){
			tarjan(e[i].v);
			low[u] = min(low[u],low[e[i].v]);
		}
		else if(vis[e[i].v]) low[u] = min(low[u],dfn[e[i].v]);
	if(low[u] == dfn[u]){
		idx++;
		int cur;
		do {
			cur = stac[top--];
			bel[cur] = idx;
			vis[cur] = false;
		} while(cur != u);
	}
}
int main(){
	scanf("%d %d",&n,&m);
	rep(i,m){
		scanf("%d %d %d %d",&x1,&a,&x2,&b);
		add(x1 + a * n,x2 + (!b) * n),add(x2 + b * n,x1 + (!a) * n);
	}
	rep(i,n * 2) if(!dfn[i]) tarjan(i);
	rep(i,n) if(bel[i] == bel[i+n]){
		printf("IMPOSSIBLE");
		return 0;
	}
	printf("POSSIBLE\n");
	rep(i,n) printf("%d ",bel[i] < bel[i+n] ? 1 : 0);
	return 0;
}