【HT-086-Div.2】嗡嗡蜜蜂

比赛传送门

更阅读体验的阅读体验

当时怎么就没想出来这个题呢，明明跟正解思路就差了一个左端点排序（我当时以为右端点排序呢）

---

我们枚举这 \(n\) 个区间，考虑当前某个区间 \(i\) 区间能取到的最大值。

对于两个区间来说，它们有三种位置关系：包含、相交、相离。我们分类讨论一下这三种情况下非共同活动范围的值。

1.两个区间相离

没什么好说的，由于不满足条件，所以它的贡献为 0。

2.两个区间相交

如图。

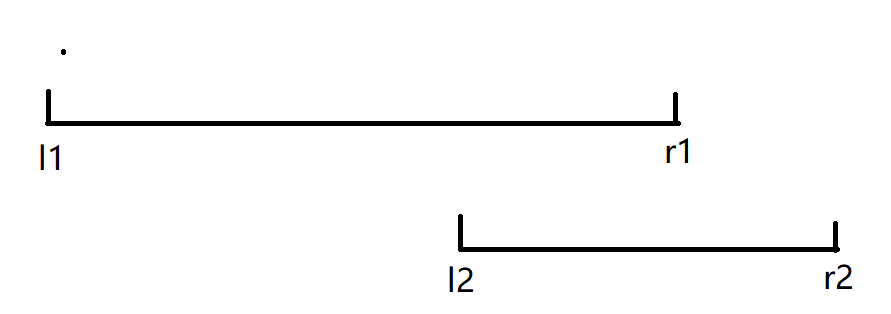
我们考虑左半边的非共同活动范围，就是 \((l_2-1)-l_1+1=l_2-l_1\)，右半边同理，是 \(r_2-(r_1+1)+1=r_2-r_1\)。两边加起来就是 \((l_2+r_2)-(l_1+r_1)\)。

3.两个区间包含

如图。

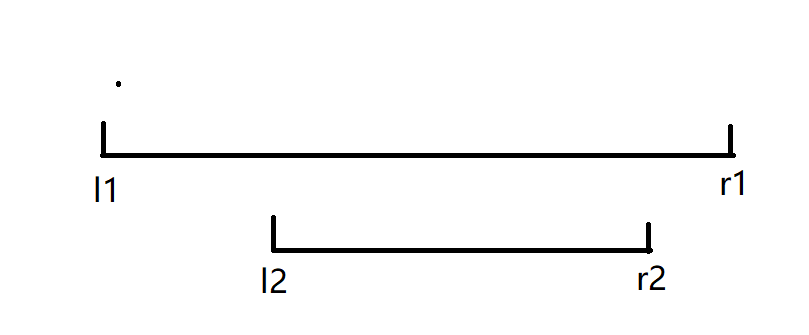
那这样的话，左半边的长度是 \((l_2-1)-l_1+1=l_2-l_1\)，右半边的长度为 \(r_1-(r_2+1)-1=r_1-r_2\)，两边加起来是 \((l_2-r_2)-(l_1-r_1)\)。

但是后两种情况对 \(r_1\) 的取值是有要求的。或者说，一个 \([l_1,r_1]\) 能与 \([l_2,r_2]\) 产生合法解，当且仅当 \(r_1 \ge l_2\) 且 \(l_1 \le l_2\)。

第二个限制好满足，我们直接按左端点排序即可。

第一个限制的话，我们可以开两个线段树，每个线段树中的区间是一段连续的右端点下标（由于右端点太大，所以需要进行离散化）。

第一个线段树记录的是右端点下标在 \([L,R]\) 里的区间中，最小的 \(l+r\)。第二个线段树记录的是右端点下标在 \([L,R]\) 里的区间中，最小的 \(l-r\)。

这样的话，考虑到第 \(i\) 个区间第二种情况时，我们就是要在第一棵线段树里找右端点下标在 \([l_i,r_i]\) 的最小的 \(l+r\)；考虑第三种情况时，我们就是要在第二棵线段树里找右端点下标在 \([r_i,len]\) 的最小的 \(l-r\)。

其中 \(len\) 为区间端点离散化完后的最大值。

考虑完第 \(i\) 个区间后，我们需要单点更新 \(r_i\) 处两棵线段树上的最小值。

剩下的内容就是写一棵单点修改区间取 \(\min\) 的线段树了。这个看代码。

时间复杂度 \(O(n \log n)\)。

代码：

T1代码

#include<bits/stdc++.h>
#define int long long
#define ls (id<<1)
#define rs ((id<<1)|1)
using namespace std;

inline int read(){
	int x=0,f=1;char c=getchar();
	while(c<48){
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}

const int N=2e5+6;
const int inf=1e16;
int n,qwq[2*N];
struct sw{
	int l,r;
}a[N];
struct seg{
	int l,r,mn;
}tr[2][8*N];

inline bool cmp(sw x,sw y){
	return x.l<y.l;
}

inline void pushup(int op,int id){
	tr[op][id].mn=min(tr[op][ls].mn,tr[op][rs].mn);
}

inline void build(int op,int id,int l,int r){
	tr[op][id].l=l,tr[op][id].r=r;
	if(l==r){
		tr[op][id].mn=inf;
		return ;
	}
	int mid=(l+r)>>1;
	build(op,ls,l,mid);build(op,rs,mid+1,r);
	pushup(op,id);
}

//单修最小值 
inline void update(int op,int id,int pos,int k){
	if(tr[op][id].l==tr[op][id].r){
		tr[op][id].mn=min(tr[op][id].mn,k);
		return ;
	}
	int mid=(tr[op][id].l+tr[op][id].r)>>1;
	if(pos<=mid) update(op,ls,pos,k);
	else update(op,rs,pos,k);
	pushup(op,id);
}

//区查最小值 
inline int query(int op,int id,int l,int r){
	if(l<=tr[op][id].l&&tr[op][id].r<=r){
		return tr[op][id].mn;
	}
	int mid=(tr[op][id].l+tr[op][id].r)>>1,ans=inf;
	if(l<=mid) ans=min(ans,query(op,ls,l,r));
	if(r>mid) ans=min(ans,query(op,rs,l,r));
	return ans;
}

signed main(){
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	n=read();
	for(int i=1;i<=n;i++){
		a[i].l=read(),a[i].r=read();
		//qwq:离散化用的数组 
		qwq[2*i-1]=a[i].l,qwq[2*i]=a[i].r;
	}
	//左端点从小到大排序 
	sort(a+1,a+n+1,cmp);
	sort(qwq+1,qwq+2*n+1);
	//离散化 
	int len=unique(qwq+1,qwq+2*n+1)-qwq-1;
	for(int i=1;i<=n;i++){
		a[i].l=lower_bound(qwq+1,qwq+len+1,a[i].l)-qwq;
		a[i].r=lower_bound(qwq+1,qwq+len+1,a[i].r)-qwq;
	} 
	build(0,1,1,len);
	build(1,1,1,len);
	//tr0:相交的情况 tr1:包含的情况 
	int ans=0;
	for(int i=1;i<=n;i++){
		//相交的情况 
		int x=query(0,1,a[i].l,a[i].r);
		ans=max(ans,qwq[a[i].l]+qwq[a[i].r]-x);
		//包含的情况 
		x=query(1,1,a[i].r,len);
		ans=max(ans,qwq[a[i].l]-qwq[a[i].r]-x);
		//不要忘记更新 
		update(0,1,a[i].r,qwq[a[i].l]+qwq[a[i].r]);
		update(1,1,a[i].r,qwq[a[i].l]-qwq[a[i].r]);
	}
	printf("%lld",ans);
	return 0;
}