一个好题
%你塞出的题,但是找不到原题,实在抱歉、、、
于是我自己建了一个题。
这是那场的题解:

题解做法是莫比乌斯反演……但是我不会这个东西,于是我考场上想的是大粪讨。
先翻译一下那个移动方式:假设你一次移动时向右走了 \(a\) 步,向下走了 \(b\) 步,那你要满足 \(a,b\) 互质。
这很显然是个计数 dp。状态很好想,就设 \(dp_{x,y}\) 表示当前走到了 \((x,y)\) 这个位置的方案数。很显然,我们只需要考虑它是从哪些格一步走过来的,然后累加从起点走到那些格的方案数就好了。
问题就在于找那些满足条件的格子了。
好像没什么思路。我们自己画一画图试试。(这里以 \((8,10)\) 为例,红色的点代表可以一步走到该点的点)
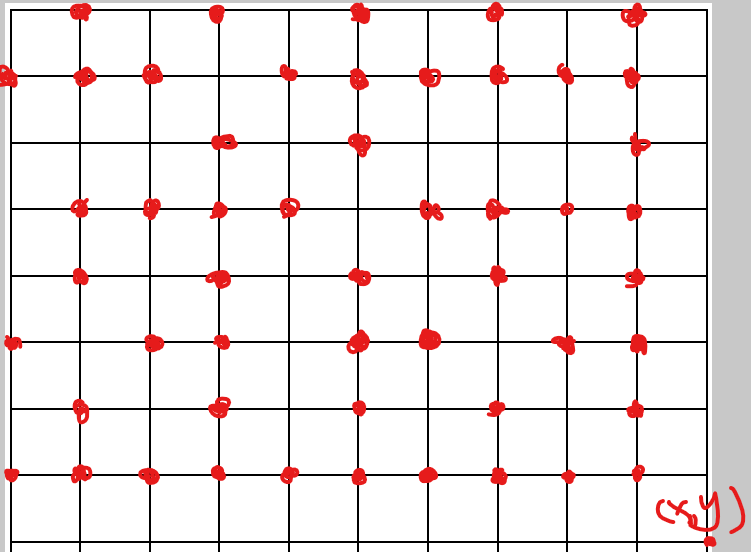
由于 \(n\) 特别小,所以我们考虑一行一行地分类讨论那些可以一步到达该点的点。
(以下及 \((xx,yy)\) 为那些正在考虑的是否可以一步到达 \((x,y)\) 的点)
我们看图。当 \((xx,yy)\) 在第 \(x-1\) 行的时候,此时 \((xx,yy)\) 要向下走 1 步,而 1 和任何数都互质,所以只要 \((xx,yy)\) 是在第 1 ~ \(y-1\) 列、第 \(x-1\) 行的点,那 \((xx,yy)\)就满足条件。图里也是都标红了的。
当 \((xx,yy)\) 在第 \(x-2/x-4/x-8\) 行时,\((xx,yy)\) 要向下走 2/4/8 步,显然不管是 2 还是 4 还是 8,只要从 \((xx,yy)\) 向右走的步数是奇数,那 \((xx,yy)\) 就是合法的。
如果 \((xx,yy)\) 在 \(x-3/x-5/x-7\) 行,那么此时 \((xx,yy)\) 要向下走 3/5/7 步。这三个数都是质数,所以只要 \((xx,yy)\) 向右走的步数不是它们的倍数,那么 \((xx,yy)\) 就合法。
最后一种情况是 \((xx,yy)\) 在 \(x-6\) 行。此时 \((xx,yy)\) 要向下走 6 步。6 是 2 和 3 的乘积,所以 \((xx,yy)\) 向右走的步数既不能是 2 的倍数也不能是 3 的倍数。也就是这个步数模 6 只能余 1 或余 5。
大家可以看看刚才的图理解一下这些结论。
于是我们考虑另开一个数组 \(sum_{j,k,i}\) 表示什么呢,当前我们计算了 1 ~ \(y-1\) 列所有点的 dp 值后,我们按行归类,第 \(i\) 行的所有点里面(当然列的范围是 \([1,y-1]\)),我们再按到当前列 \(y\) 的横向距离分类。\(sum_{j,k,i}\) 表示第 \(i\) 行这些点里,横向距离对 \(j\) 取余后余数是 \(k\) 的所有点的 dp 值之和。(怎么这么绕)
我们如果已经知道怎么想办法处理并实时更新 \(sum\) 数组,那我们就可以对于每个在考虑的点 \((x,y)\),\(O(n)\) 地转移 dp 值了。上面分讨的就是它对于不同的行的转移过程。
那我们咋更新 \(sum\) 捏?
首先 \(sum\) 收录的点里,列坐标要比当前点的列坐标至少小 1。所以当我们只有考虑完这一列时,才能用这一列的 \(dp\) 值更新 \(sum\)。更新完后就到了下一列了,所以当前更新 dp 值的点的列坐标又变成比当前考虑的列坐标小一的了。
然后,当我们的列坐标从 \(y\) 变到 \(y+1\) 时,我们所有已收录的点的横向步数会整体加一,模 \(j\) 的模数也会变化,会整体加一后再模 \(j\)。比如当前一些点到 \(y\) 的横向距离模 5 余 3,那当 \(y -> y+1\) 时,这个横向距离模 5 就余 4。
如果当前的横向距离模 5 余 4,那么 \(y -> y+1\) 后横向距离就会模 5 余 0。
所以我们如果单独开一个用于转移的数组 \(b\) 存储 \(y -> y+1\) 后的 \(sum\) 数组的话,那么 \(b_{j,k,i}=sum_{j,(k-1) \mod j,i}\)。
这样我们这个做法的整体思路就说完了。由于我们转移 \(sum\) 数组的时间复杂度是 \(O(n^3)\) 的,所以这种做法的时间复杂度是 \(O(n^3m)\) 的。
其他细节请见代码:
代码
#include<bits/stdc++.h>
#define int long long
#define _(x,y) ((((x)-(y))%mod+mod)%mod)
#define __(x,y) ((((x)+(y))%mod+mod)%mod)
#define ___(x,y) ((((x)*(y))%mod+mod)%mod)
using namespace std;
inline int read(){
int x=0,f=1;char c=getchar();
while(c<48){
if(c=='-') f=-1;
c=getchar();
}
while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
const int N=10;
const int M=1e5+5;
const int mod=998244353;
int n,m,dp[N][M],sum[N][N][N],b[N][N][N],mus[N][N][N];
inline void update(){
//update:当 y -> y+1时,我们要更新好 sum 数组
for(int i=0;i<=n;i++){
for(int j=1;j<=n;j++){
//模数变成 0 的情况有点特殊,这里我拿出去考虑的
b[j][0][i]=sum[j][j-1][i];
for(int k=1;k<j;k++){
b[j][k][i]=sum[j][k-1][i];
}
}
}
//用 b 数组更新 sum 数组
for(int i=0;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=0;k<j;k++){
sum[j][k][i]=b[j][k][i];
}
}
}
}
signed main(){
n=read(),m=read();
//初始化
dp[0][0]=1;
//由于我们当前相当于考虑的是第0列,横向距离是 0,所以更新sum[i][0][0]
for(int i=1;i<=n;i++){
sum[i][0][0]=1;
}
//这里先枚举列后枚举行是为了保证y单调递增,正好顺应sum数组的更新方式
for(int y=1;y<=m;y++){
update();
for(int i=0;i<=n;i++){
for(int k=1;k<=i;k++){
//这一段分讨同题解的分讨部分
if(k==1){
dp[i][y]=__(dp[i][y],sum[1][0][i-1]);
}
else if(k==2){
dp[i][y]=__(dp[i][y],sum[2][1][i-2]);
}
else if(k==3){
dp[i][y]=__(dp[i][y],sum[3][1][i-3]+sum[3][2][i-3]);
}
else if(k==4){
dp[i][y]=__(dp[i][y],sum[4][1][i-4]+sum[4][3][i-4]);
}
else if(k==5){
dp[i][y]=__(dp[i][y],sum[5][1][i-5]+sum[5][2][i-5]+sum[5][3][i-5]+sum[5][4][i-5]);
}
else if(k==6){
dp[i][y]=__(dp[i][y],sum[6][1][i-6]+sum[6][5][i-6]);
}
else if(k==7){
dp[i][y]=__(dp[i][y],sum[7][1][i-7]+sum[7][2][i-7]+sum[7][3][i-7]+sum[7][4][i-7]+sum[7][5][i-7]+sum[7][6][i-7]);
}
else if(k==8){
dp[i][y]=__(dp[i][y],sum[8][1][i-8]+sum[8][3][i-8]+sum[8][5][i-8]+sum[8][7][i-8]);
}
}
}
//同题解
//需要在当前列所有行都考虑完后更新也说原因了,否则你实时更新不能保证所有点都是列坐标在 1 ~ y-1的
for(int i=0;i<=n;i++){
for(int k=1;k<=n;k++){
sum[k][0][i]=__(sum[k][0][i],dp[i][y]);
}
}
}
int ans=dp[n][m];
printf("%lld\n",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号