P10277 [USACO24OPEN] Bessie's Interview S
闲话:机房模拟赛出的,后来补题的时候纯模拟跑过去了……还跑出了我OI生涯第一个最优解,不是?
那我们就说说纯模拟做法。
首先第一问很简单,直接用一个优先队列存当前面试官的编号,以及面试官面试完的时间,模拟这个过程就好。
相信很多人都想到了并查集。但是并查集很容易被证伪,请看以下数据:
(以下我们用方块长度表征面试时间长短)
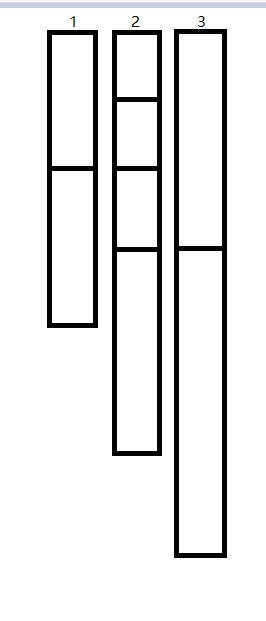
我们发现,1 是最优解,因为 1 和 2 有一段是齐平的,所以 1 和 2 后面接的东西是可以互换的,所以 2 也是最优解。
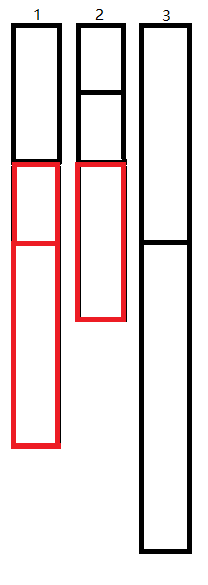
但是 3 和 2 虽然有一段是齐平的,2 从 1 上传来的最优解并不能传递到 3 上。因为 2 换完以后和 3 的齐平面就没了。
但是我们反过来看,如果某种情况下 3 是最优解的话,1 是能通过 2 传递来最优解的。因为我们发现,后齐平面以后的部分交换后,前齐平面并不会改变。
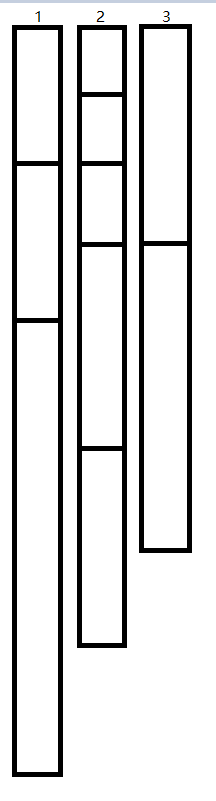

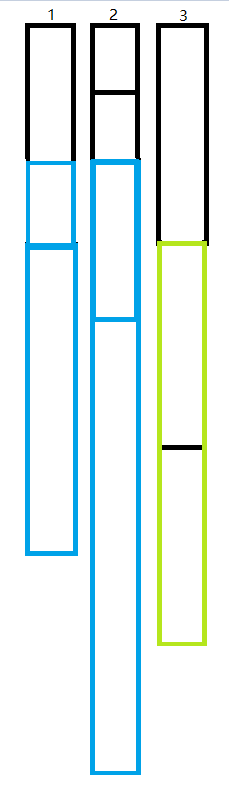
看完这个例子后,我们发现:后齐平面改变并不会影响前齐平面,但是前齐平面的改变会影响后齐平面。
所以我们在原先优先队列模拟的基础上,开一个 vector 数组 \(g\) 和变量 \(newn\),当优先队列里有多个相同的面试结束时间,就让 \(newn++\),再让 \(g_{newn}\) 把这些有同一齐平面的面试官的编号记录下来。
同时我们要继续模拟,让优先队列把这之后面试的奶牛都随便找个面试官开始面试。
注意,最后可能有多个面试官的结束时间相同且最短。这里我的解决方案是新开一个 \(newn\),然后仍然用 \(g_{newn}\) 把这些面试官的编号存下来。
最后我们按 \(newn\) 从大到小倒序枚举 \(g\) 数组,让后面齐平面的合法状态传递到前面的齐平面上去。
(感觉说的不太清楚,就是说,如果某个齐平面上有一个编号可以,那这个齐平面上的所有编号都是合法的。并且后齐平面交换不影响前齐平面,所以这个合法状态可以通过后面齐平面的某个编号,传递给这个编号前面与它共齐平面的编号上)
最后输出所有编号是否合法即可。
因为 \(g\) 中最多有 \(n\) 个元素,所以最终时间复杂度是 \(O(n \log n)\) 的。
P10277正常版
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x=0,f=1;char c=getchar();
while(c<48){
if(c=='-') f=-1;
c=getchar();
}
while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
const int N=3e5+5;
int n,k,a[N],newn,ok[N];
struct WS{
int lst,id;
bool operator <(const WS Ws)const{
return lst>Ws.lst;
}
};
priority_queue<WS> q;
//q:用来模拟的优先队列
vector<int> g[N];
//g,newn:同题解
signed main(){
n=read(),k=read();
for(int i=1;i<=n;i++){
a[i]=read();
}
//初始化要让对应编号的奶牛来面试
for(int i=1;i<=k;i++){
q.push((WS){a[i],i});
}
for(int i=k+1;i<=n;i++){
int lst=q.top().lst,id=q.top().id;
q.pop();
q.push((WS){lst+a[i],id});
if(!q.empty()&&q.top().lst==lst){//处理多人同时面试完的情况
newn++;
g[newn].push_back(id);
while(!q.empty()&&q.top().lst==lst){
int ID=q.top().id;
g[newn].push_back(ID);
i++;
if(i>n) break;//注意特判i的边界
q.push((WS){lst+a[i],ID});
q.pop();
}
}
}
//我们最后把最小的所有解法扔进g中新开的 newn 里(虽然这步好像没什么必要)
++newn;
int ans1=0;
ans1=q.top().lst;
int id=q.top().id;
q.pop();
ok[id]=1;
g[newn].push_back(id);
while(!q.empty()&&q.top().lst==ans1){
int ID=q.top().id;
g[newn].push_back(ID);
ok[ID]=1;
q.pop();
}
for(int i=newn;i>=1;i--){
int fl=0;
for(int j=0;j<g[i].size();j++){//判断当前齐平面是否有可以最优解的
if(ok[g[i][j]]){
fl=1;break;
}
}
if(!fl) continue;
for(int j=0;j<g[i].size();j++){
ok[g[i][j]]=1;
}
}
//输出答案
printf("%lld\n",ans1);
for(int i=1;i<=k;i++){
printf("%lld",ok[i]);
}
printf("\n");
return 0;
}
但是后来某个@Deity_Ling 非要跟我卡常……于是最优榜第一面最终变成了这个样子。
奉上卡常后的最优解代码:
P10277卡常版
#include<bits/stdc++.h>
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1000096,stdin),p1==p2)?EOF:*p1++)
using namespace std;
char *p1,*p2,buf[1000100];
inline int read(){
int x=0,f=1;char c=gc();
while(c<48){
if(c=='-') f=-1;
c=gc();
}
while(c>47) x=(x<<1)+(x<<3)+(c^48),c=gc();
return x*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else write(x/10),putchar(x%10+'0');
}
const int N=3e5+5;
int n,k,a[N],newn;
bitset<N> ok;
struct WS{
long long lst;
int id;
bool operator <(const WS Ws)const{
return lst>Ws.lst;
}
};
priority_queue<WS> q;
vector<int> g[N];
signed main(){
n=read(),k=read();
for(register int i=1;i<=n;i++){
a[i]=read();
}
for(register int i=1;i<=k;i++){
q.push((WS){a[i],i});
}
for(register int i=k+1;i<=n;i++){
long long lst=q.top().lst;int id=q.top().id;
q.pop();
q.push((WS){lst+a[i],id});
if(!q.empty()&&q.top().lst==lst){
newn++;
g[newn].push_back(id);
while(!q.empty()&&q.top().lst==lst){
int ID=q.top().id;
g[newn].push_back(ID);
i++;
if(i>n) break;
q.push((WS){lst+a[i],ID});
q.pop();
}
}
}
++newn;
long long ans1=0;
ans1=q.top().lst;
int id=q.top().id;
q.pop();
ok[id]=1;
g[newn].push_back(id);
while(!q.empty()&&q.top().lst==ans1){
int ID=q.top().id;
g[newn].push_back(ID);
ok[ID]=1;
q.pop();
}
for(register int i=newn;i>=1;i--){
int fl=0;
for(register int j=0;j<g[i].size();j++){
if(ok[g[i][j]]){
fl=1;break;
}
}
if(!fl) continue;
for(register int j=0;j<g[i].size();j++){
ok[g[i][j]]=1;
}
}
printf("%lld\n",ans1);
for(register int i=1;i<=k;i++){
write(ok[i]);
}
printf("\n");
return 0;
}
另外,奉上自己造出来的几个小数据,方便大家调试。
in1:
13 6
18 14 9 1 9 11 21 9 10 20 29 29 6
ans1:
19
001010
in2:
12 5
13 28 1 13 3 16 15 6 7 16 1 6
ans2:
19
10011
in3:
5 2
17 17 18 18 18
ans3:
35
11
in4:
6 3
6 17 17 17 17 17
ans4:
23
100




 浙公网安备 33010602011771号
浙公网安备 33010602011771号