P10279 [USACO24OPEN] The 'Winning' Gene S
本篇题解参照的是这位大佬的题解。(看不到的话点这个)。图片参考这篇题解。
这个题面真的很绕。简化一下就是说,对于一个 \((K,L)\),要在原串里选出所有 \(K-mer\),然后对于每个 \(K-mer\),要找到字典序最小的长度为 \(L\) 的串串(有多个就选最靠左的)。然后我们把这个串串的起始位置丢到集合 \(P\) 里。
最后,这个集合 \(P\) 里会有所有 \(K-mer\) 扔进去的起始位置。当然,一部分起始位置会重复,所以 \(P\) 的大小不确定。
基本思路
我们发现这个 \(K\) 似乎没什么用……所以我们考虑一种常见的思路,叫做拆贡献。我们枚举 \(L\),接下来我们讨论的,都是基于特定的 \(L\) 之上的。
对于一个起始位置 \(pos\),它会被怎样的 \(K\) 丢进集合呢?显然,它要在某个 \(K-mer\) 里字典序最小才会有贡献。那也就是说,在某个区间里,不能有比它字典序更小的起始位置出现。
我们可以跑一遍单调栈,预处理出 \(l_{pos},r_{pos}\),分别表示左 / 右边第一个字典序小于 \(pos\) 的起始位置。
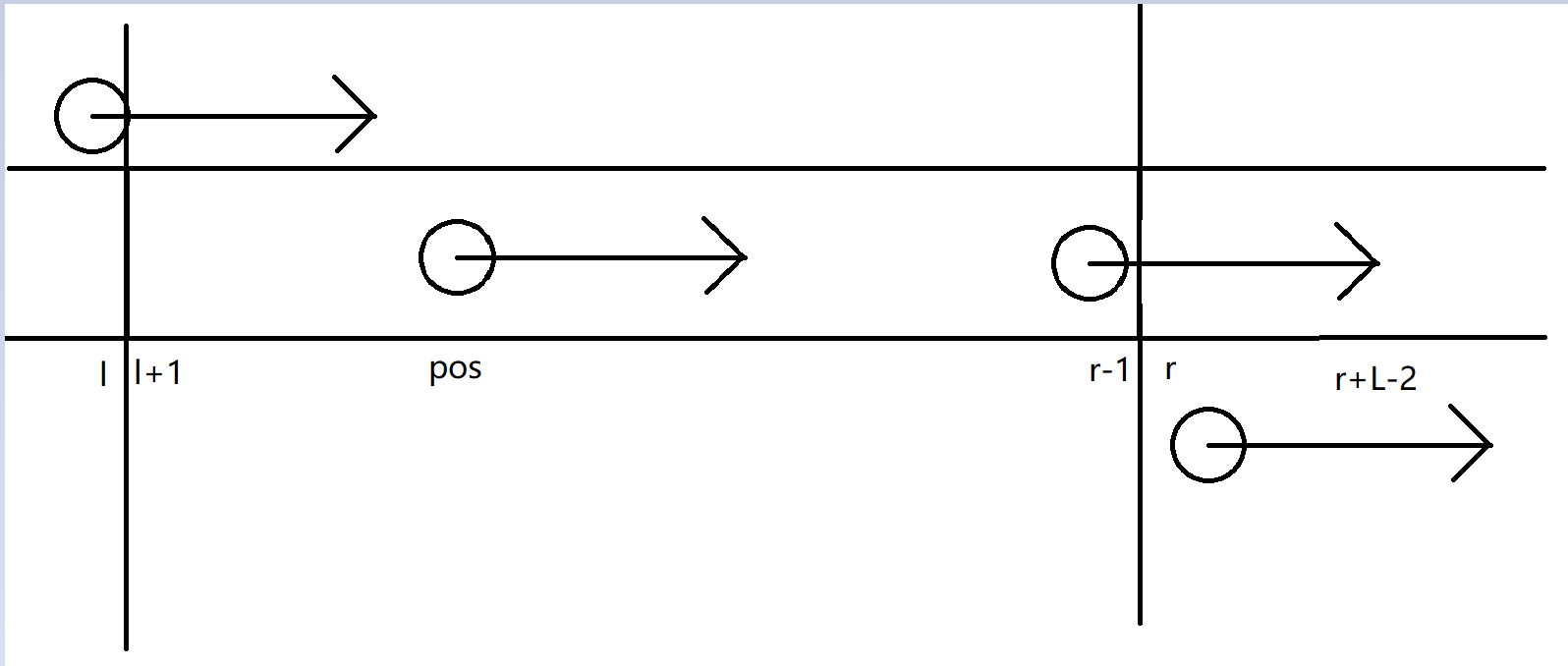
很显然,这样的话 \(K\) 的最小值取 \(L\)(即只有它一个串的情况),\(K\) 的最大值就是蓝色区间的长度,即 \(r_{pos}+L-2-l_{pos}\)。
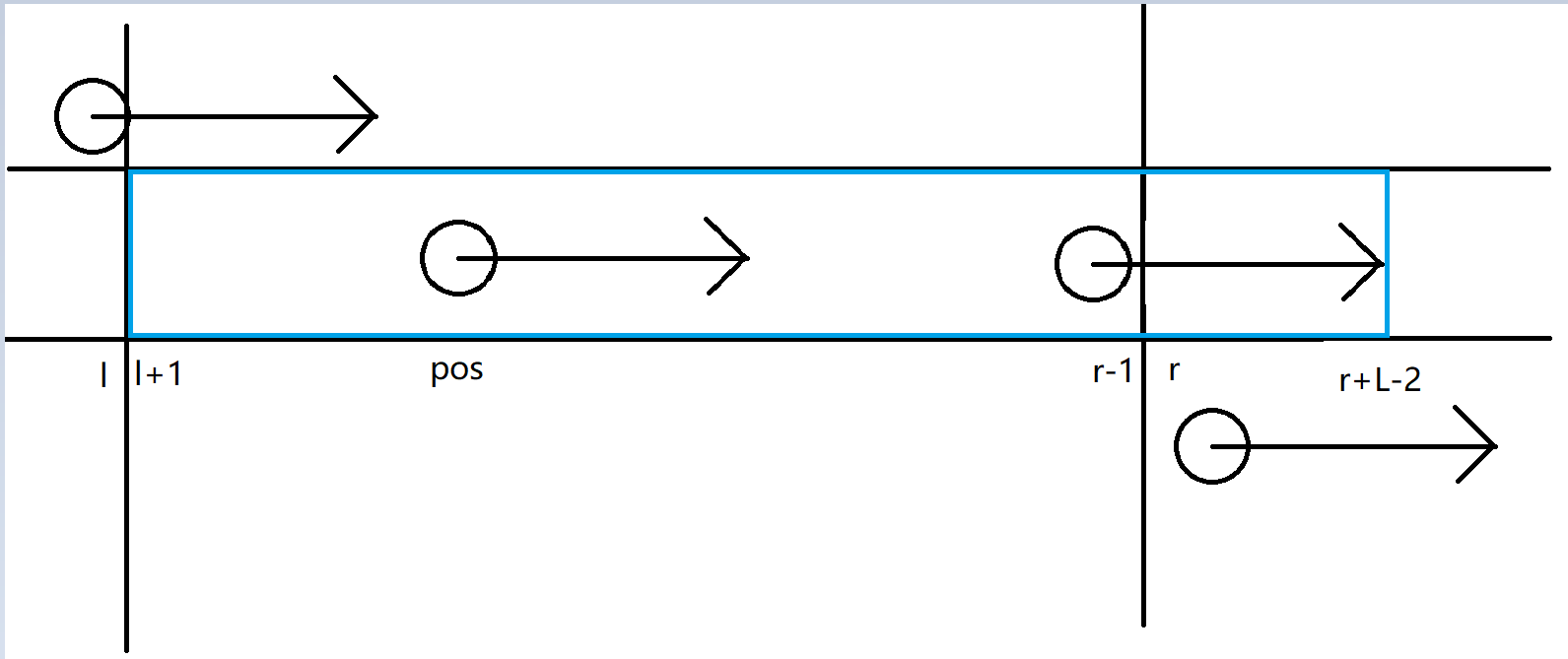
落在这个范围里的 \(K\),它总会有一个或多个 \(K-mer\),使得字典序最小的长度是 \(L\) 的串串开头是 \(pos\)。这样的话 \(pos\) 就会被扔进集合里了。
所以我们可以对 \([L,r_{pos}+L-l_{pos}-2]\) 进行区间加 1,这个用差分做就好。
(有些人就是数据结构学傻了,差分都用线段树写)
最后,我们用 \(ans_{K,L}\) 表示 \((K,L)\) 这个数对被贡献了多少次,也就是这个数对下集合里会有多少个数。我们的差分操作就是在这个数组上进行的。
我们另开一个桶 \(sum_{i}\) 表示集合大小为 \(i\) 的数对有几个。显然最后输出 \(sum_{1,2, \cdots ,n}\) 即可。
如何求字典序
大体思路有了,但是我们很快意识到一个严重的问题:我们枚举 \(L\),并且单调栈的时间复杂度已经是 \(O(n^2)\) 的了,而在做单调栈时要判断字典序大小,正常比较字典序是 \(O(n)\) 的,所以我们这样做的时间复杂度是 \(O(n^3)\) 的,正常情况下过不去。
那怎么办呢?我们考虑对求字典序的过程剪枝。
剪枝 1(记忆化)
字典序的比较规则是找第一个不相同的字符并比较大小。由于正常情况下我们是正序枚举 \(L\) 的,所以对于两个起始位置 \(p_1,p_2\),如果之前长度更短的情况下已经比较出来了大小,那我们现在就无须比较了。
具体实现上也很简单:单独开一个数组 \(f_{p1,p2}\) 记录当前是否已经比较出来了胜负,0 表示没有,1 表示字典序上 \(p_1>p_2\),-1 表示字典序上 \(p_1<p_2\)。每次判断字典序时提前判断即可。
但是这样会被一些特殊的构造卡掉:
aaaa...ab
aaaa...aa
显然我们直到发现 a<b 后才能比较大小。于是我们有了剪枝2。
剪枝 2(当前弧优化)
类似P7771里记录当前第一条没有被走过的边,我们记录 \(h_{p1,p2}\) 表示当前的 \(p1,p2\) 最后一个已被比较的位置是什么。这样我们比较字典序的时候,直接比较 \(h_{p1,p2}+1\) ~ \(L\) 的位置即可。
总之我们终于可以 AC 这个题了。
代码:
P10279
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x=0,f=1;char c=getchar();
while(c<48){
if(c=='-') f=-1;
c=getchar();
}
while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
const int N=3e3+3;
int n,ans[N][N],l[N],r[N],f[N][N],h[N][N],sum[N];
char s[N],ch[N][N];
stack<int> st;
//ch[i][j]:在第i个位置扩展j位,最后一位是什么
//ans[k][l]:有多少初始位置贡献了(k,l)二元组
inline bool cmp1(int p1,int p2,int len,char s1[],char s2[]){
//记忆化
if(f[p1][p2]==1) return 1;
if(f[p1][p2]==-1) return 0;
//当前弧优化
for(int i=h[p1][p2]+1;i<=len;i++){
if(s1[i]>s2[i]){
f[p1][p2]=1;
return 1;
}
else if(s1[i]<s2[i]){
f[p1][p2]=-1;
return 0;
}
}
//记得更新f,h
h[p1][p2]=len;
return 0;
}
//同cmp1
inline bool cmp2(int p1,int p2,int len,char s1[],char s2[]){
if(f[p1][p2]==1) return 1;
if(f[p1][p2]==-1) return 0;
for(int i=h[p1][p2]+1;i<=len;i++){
if(s1[i]>s2[i]){
f[p1][p2]=1;
return 1;
}
else if(s1[i]<s2[i]){
f[p1][p2]=-1;
return 0;
}
}
h[p1][p2]=len;
return 1;
}
signed main(){
n=read();
scanf("%s",s+1);
for(int len=1;len<=n;len++){
//len同题解里的L
for(int i=1;i+len-1<=n;i++){
//每次len+1时显然只会扩展1位
ch[i][len]=s[i+len-1];
l[i]=0,r[i]=0;
}
//单调栈处理l,r数组
while(!st.empty()) st.pop();
//解释一下两个cmp函数:
//在字典序相同的情况下,优先取左边的串
//所以从左往右的单调栈是单调不升的,从右往左的单调栈是单调递减的
for(int i=1;i+len-1<=n;i++){
while(!st.empty()&&cmp1(st.top(),i,len,ch[st.top()],ch[i])){
st.pop();
}
if(!st.empty()) l[i]=st.top();
else l[i]=0;
st.push(i);
}
while(!st.empty()) st.pop();
for(int i=n-len+1;i>=1;i--){
while(!st.empty()&&cmp2(st.top(),i,len,ch[st.top()],ch[i])){
st.pop();
}
if(!st.empty()) r[i]=st.top();
else r[i]=n-len+2;
st.push(i);
}
//区间加
for(int i=1;i+len-1<=n;i++){
ans[len][len]++;ans[r[i]+len-l[i]-1][len]--;
}
}
//统计答案
for(int j=1;j<=n;j++){
for(int i=1;i<=n;i++){
ans[i][j]+=ans[i-1][j];
sum[ans[i][j]]++;
}
}
for(int i=1;i<=n;i++){
printf("%lld\n",sum[i]);
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号