P8269 [USACO22OPEN] Visits S

题目传送门

博客传送门

首先，每头牛牛都只有一个拜访对象，所以如果考虑图论建模的话，相当于每个点出度都是 1。这相当于图是个基环树森林（注意不只有一棵基环树），而且每个基环树都是内向基环树。

而且我们注意到有个特殊点，建出来的图是很多个环，就更加坚定了我们往基环树那块考虑的想法。我们把一个基环树的图画出来：

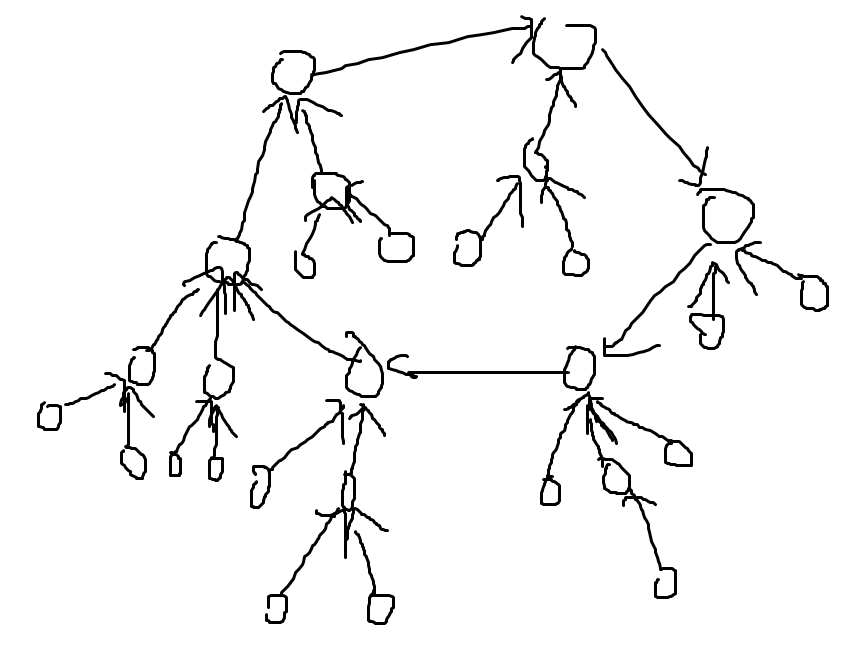
（很像你妈妈的钥匙串有木有）

然后转换一下原题的题意。既然决定图论建模了，那原题的 \(a_i\) 就相当于 \(i -> a_i\) 建边，边权是 \(v_i\)。至于排列，其实就是个行动顺序表，问我们如何安排行动顺序会让最终贡献最大。

对于不在环里的节点，显然不断让入度为 0 的点行动是更优的。首先一个点出去拜访以后就不可能回来，其次对于下图的情况，先让连向 \(v\) 的点拜访 \(v\)，然后 \(v\) 再去拜访别人，比先让 \(v\) 拜访别人，多了 \(w_1+w_2+\cdots+w_k\) 的贡献。

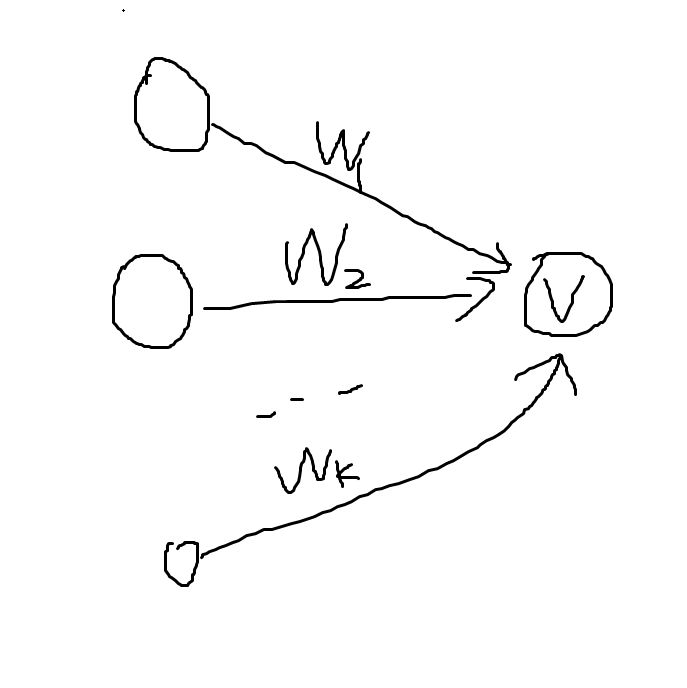
所以对于环外的部分，直接贪心地进行拓扑排序，累加边权即可。

这样我们就只剩下基环树森林里仅存的几个环了。

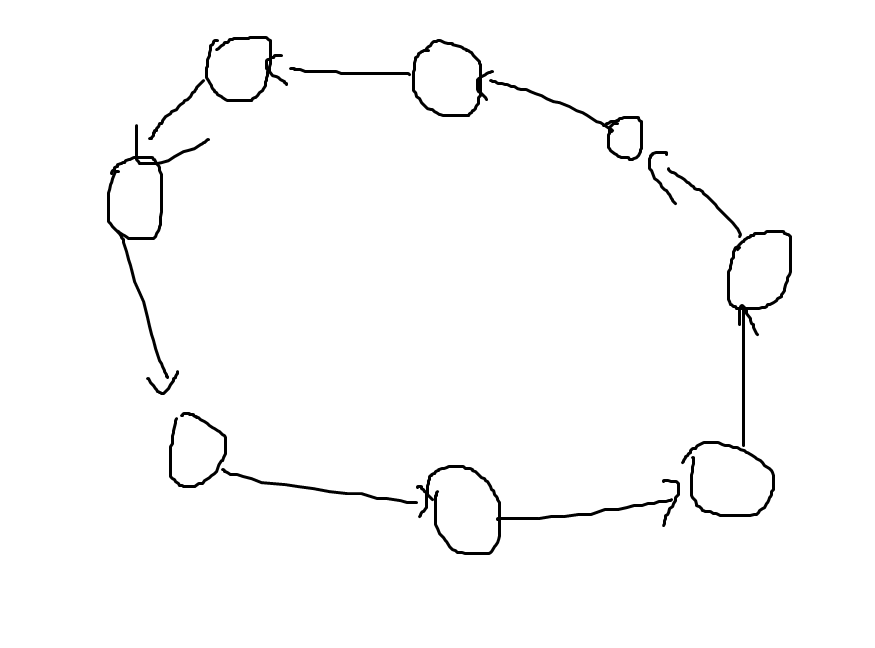
对于一个环来说，显然你是注定无法让它们都能统计贡献的。你可以自己在脑子里想象这些点逐个移动到它的拜访点，然后你就会发现注定有一个点的拜访点已经挪走了。

刚才那一通模拟后你还能得到，如果这个环有 \(m\) 条边，那你一定可以统计 \(m-1\) 条边的贡献，而且这样一定是比 \(m-2\) 条边或者更往下的情况更优。那些情况一定是如下的图所展示的：

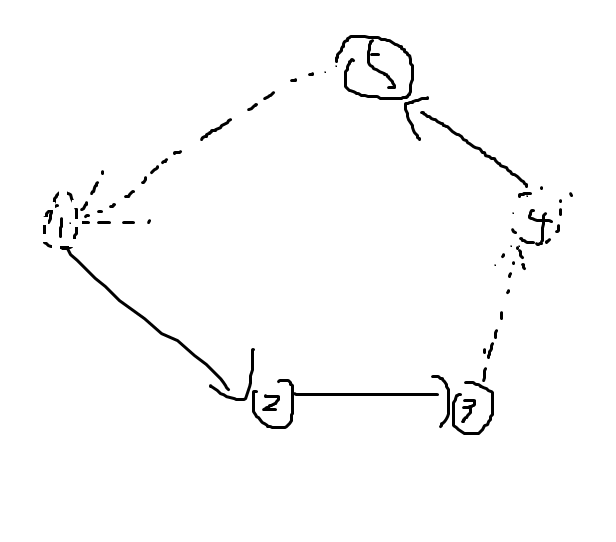
也就是 1->2,2->3,4->5,3->4,5->1。那你一定不如 1->2,2->3,3->4,4->5,5->1 或是 4->5,5->1,1->2,2->3,3->4 优。

既然这样，那就相当于我们要在这个环上舍弃一条边。贪心一下，我们舍弃这个环上的最小边。这棵基环树的贡献就是它边权的总和减掉被舍弃的边之边权。

注意原图里有多个基环树，也会有多个环，要将它们被舍弃的边求一个 sum，然后统一减掉。

代码：

P8269

#include<bits/stdc++.h>
#define int long long
using namespace std;

inline int read(){
	int x=0,f=1;char c=getchar();
	while(c<48){
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}

const int N=1e5+5;
const int inf=1e16;
int n,h[N],tot,in[N],p[N],W[N],vis[N],mi=inf;
queue<int> q;
struct Nahida{
	int u,v,w,nxt;
}e[N];

inline void add(int u,int v,int w){
	e[++tot]={u,v,w,h[u]};h[u]=tot;in[v]++;
}

inline void dfs(int u){
	vis[u]=1;
	for(int i=h[u];i;i=e[i].nxt){
		int v=e[i].v;
		mi=min(mi,e[i].w);
		if(vis[v]) continue;
		dfs(v);
	}
}

signed main(){
	n=read();
	int sum=0;
	for(int i=1;i<=n;i++){
		int v=read(),w=read();
		p[i]=v,W[i]=w;
		sum+=W[i];
		add(i,v,w);
	}
	for(int i=1;i<=n;i++){
		if(!in[i]){
			q.push(i);
		}
	}
	int ans=0;
	while(!q.empty()){
		int u=q.front();q.pop();
		int v=p[u];
		if(in[v]){
			in[v]--;
			if(!in[v]){
				q.push(v);
			}
		}
	}
	int misum=0;
	for(int i=1;i<=n;i++){
		if(in[i]&&!vis[i]){
			mi=inf;
			dfs(i);
			misum+=mi;
		}
	}
	ans=sum-misum;
	printf("%lld",ans);
	return 0;
}