P5322 [BJOI2019] 排兵布阵

题目传送门

博客传送门

我们浏览一遍测试点，发现了一个 \(s=1\) 的特殊性质。先考虑这一性质。

\(s=1\)特殊性质

如果我们当前第 \(i\) 座城市的兵力数量足够时，添加兵力显然不优。而如果兵力不够，我们的最优策略挺显然的，要么添加兵力使其恰好足够，要么干脆就不要这个城市。

换句话说，我们对一个城市的决策只有选与不选两种，选的话需要花费一定的体积，同时获得一定的价值。

听我这么一描述，是不是感觉这就是个很板的01背包？对的对的，这个部分分就是个01背包板子……忘记01背包的可以移步01背包基础

而那个兵力限制 \(m\)，往这个方向上考虑，其实就是个背包最大容量 \(V\)。

特殊性质代码也贴在这里，希望有助于大家理解。

P5322特殊性质

#include<bits/stdc++.h>
#define int long long
using namespace std;

inline int read(){
	int x=0,f=1;char c=getchar();
	while(c<48){
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}

const int N=120;
const int M=2e4+4;
int S,n,m,w[N],v[N],dp[M];

signed main(){
	S=read(),n=read(),m=read();
	int W=m;
	//不同于我当时的博文，这里的w数组是代价，v数组是价值 
	for(int i=1;i<=n;i++){
		int x=read();
		//根据题意，第i座城市恰巧被占领的兵力是2*a[i]+1 
		w[i]=((x<<1)|1),v[i]=i;
	}
	//01背包模版 
	for(int i=1;i<=n;i++){
		for(int j=W;j>=w[i];j--){
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
	int ans=dp[m];
	printf("%lld",ans);
	return 0;
}

正解

那既然这个部分分是个背包dp，我们合理猜测本题也是个dp，搞不好还是背包dp。

考虑分组背包。简单来说，既然对决是独立的，我们对于某座城池，首先可以将 \(s\) 个人的驻守兵力从小到大排序。记排序后的数组为 \(b\)。

接下来的过程类似于你做题时拿部分分。

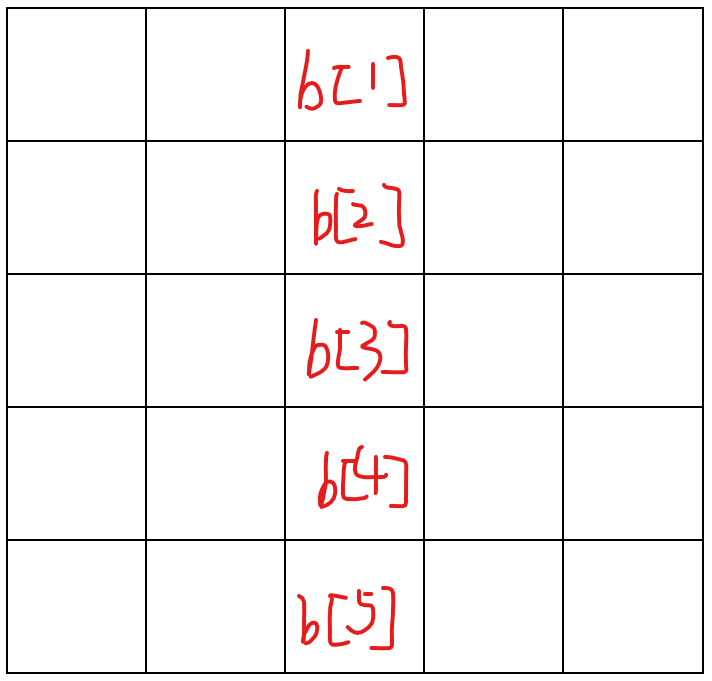
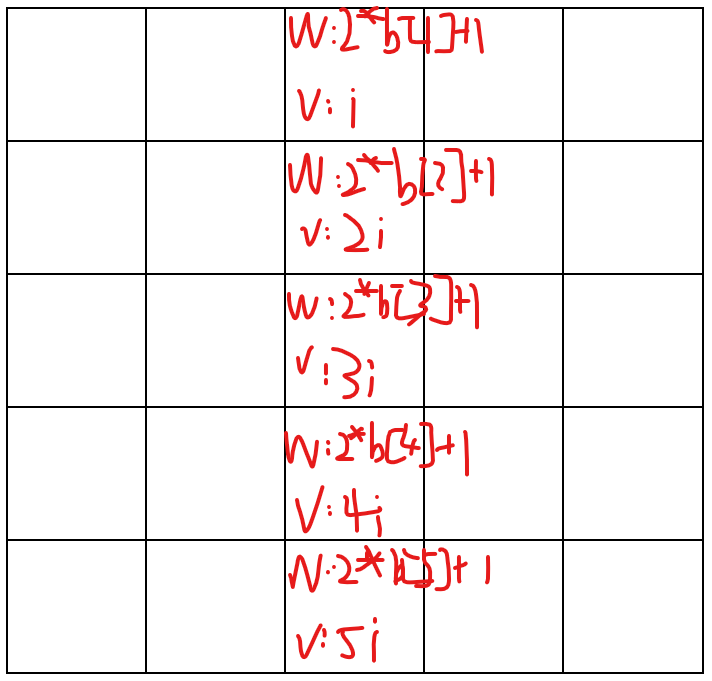
对于某个城市 \(i\)，因为 \(b_1 \le b_2 \le \cdots b_s\) ，所以如果我们现在的驻扎兵力刚好可以拿下 \(b_j\) 的话，那它一定能且只能拿下 \(b_1,b_2,\cdots,b_j\)。

所以我们拆物品方法有所不同：对于\(i\) 城市兵力第 \(j\) 小的那个对应得物品，我们让它的体积是 \(2*b_j+1\)，价值是 \(j \times i\)，如上图所示。

（类似于你拿部分分，除非特殊性质，否则你拿到越靠后的分，用的时间一般越长，但拿到的分值也会越高。而且你能解决后面的部分分，也就能解决前面的部分分）

就像你做题的时候，一道题目只会有一个得分，对于 \(i\) 城市，贡献只能有一个，所以这个分组背包的组就是每个城市，里面的物品就是刚才拆出来的 \(s\) 个。我们只能选择一个物品的价值作为这个城市的最终贡献。

总之分析到这里，本题就是个很板的背包dp，仅此而已。

代码：

P5322

#include<bits/stdc++.h>
#define int long long
using namespace std;

inline int read(){
	int x=0,f=1;char c=getchar();
	while(c<48){
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}

const int N=120;
const int M=2e4+4;
int S,n,m,w[N],v[N],dp[M],a[N][N],b[N],W[N][N],V[N][N],DP[N][M];

signed main(){
	S=read(),n=read(),m=read();
	for(int i=1;i<=S;i++){
		for(int j=1;j<=n;j++){
			a[i][j]=read();
		}
	}
	//拆分物品 
	for(int i=1;i<=n;i++){
		for(int j=1;j<=S;j++){
			b[j]=a[j][i];
		}
		sort(b+1,b+S+1);
		for(int j=1;j<=S;j++){
			W[i][j]=2*b[j]+1,V[i][j]=i*j;
		}
	}
	//分组背包 
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			for(int k=0;k<=S;k++){
				//k=0时的物品价值是0，代价是0，相当于根本不要i城市的情况 
				if(j>=W[i][k]){
					DP[i][j]=max(DP[i][j],DP[i-1][j-W[i][k]]+V[i][k]);
				}
			}
		}
	}
	int ans=DP[n][m];
	printf("%lld",ans);
	return 0;
}