P2272 [ZJOI2007] 最大半连通子图

闲聊：最近好像一直在写题，好久没补题解了qwq，今天来一发。

以及，不会缩点的请先移步P3387

---

题目传送门

博客传送门

思路

首先呢，如果原图里存在强连通分量，那么它们首先是半联通的（任意两点间都可以相互到达）。

其次，如果外面有其他点 \(u\) 能到达其中一点 \(v\) ，显然 \(u\) 也能到达强联通分量里其他任意一点。如果是其中一点 \(v\) 能到达外面某点 \(u\) ，那么显然其他强联通分量里的点也能到达 \(u\) 。

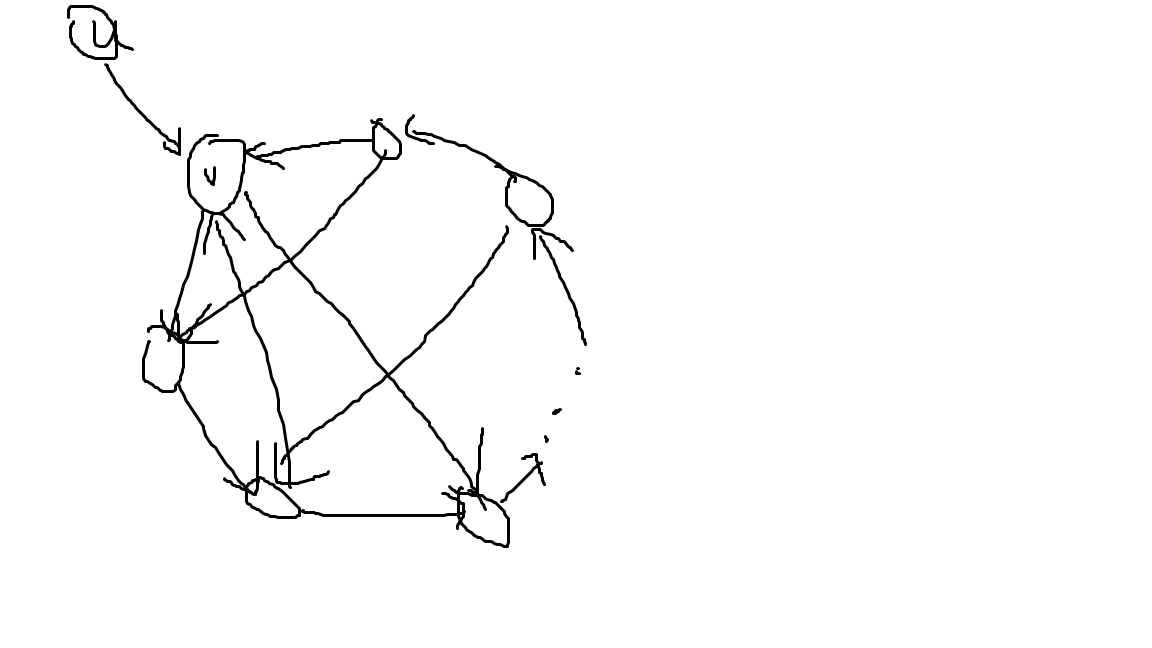
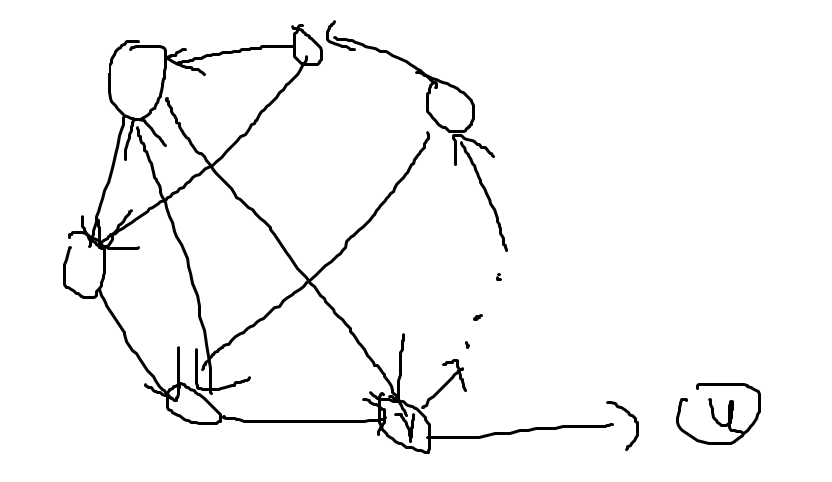
于是，如果一些点同时归属于一个强联通分量，那么如果其中的一个点被选进子图了，把整个强联通的部分都选进去一定是更优的。

这样本题的第一步就是缩点，缩完后的图一定是个 DAG 。我们接着在 DAG 上跑带点权的原问题就好了。

（以下的点编号均为缩点后的新点的编号）

玩了几组数据后，我们发现 DAG 的半联通子图似乎一定是个单向的链。其实也很好理解，如下图所示，如果某处点存在如下的两种分支，显然 B 和 C 点是无法互相到达的。

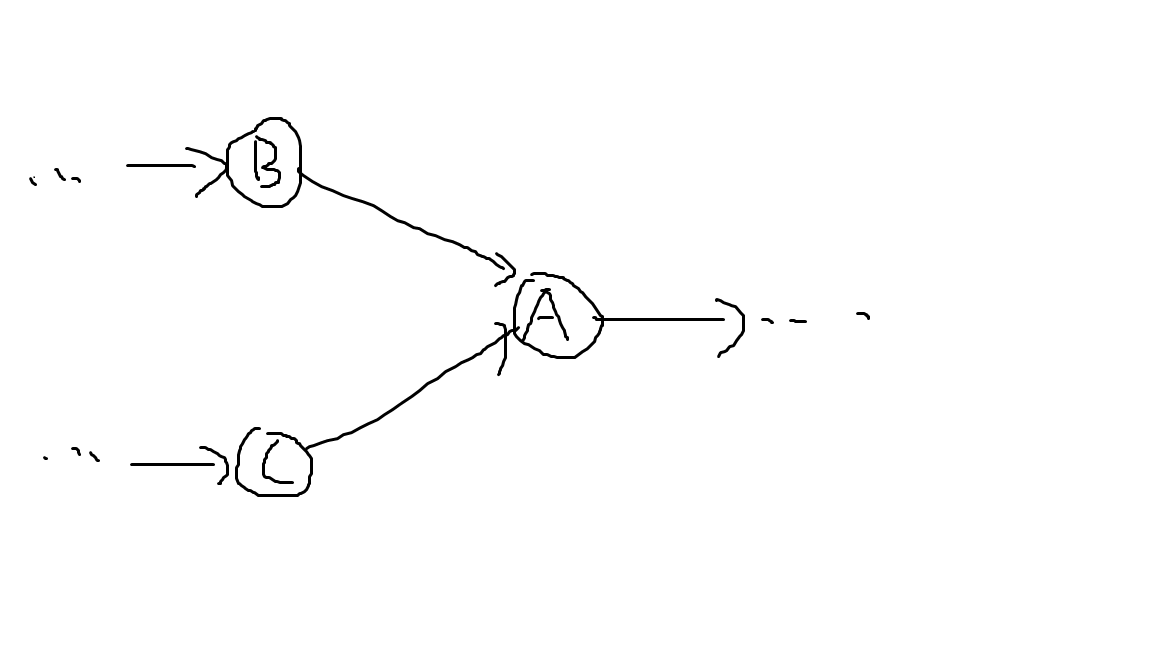
所以问题就变得特别简单了：拓扑dp找带权最长路及最长路计数， \(dp_{i}\) 表示走到 \(i\) 号点的带权最长路是多少， \(sum_{i}\) 则表示走到 \(i\) 号点的最长路条数是多少。

这样更新的式子就是这两种（ \(w_{v}\) 表示新图里的 \(v\) 点里有多少旧图里的点，也就是我们说的点权）：

\[\begin{cases} dp_{v}=dp_{u}+w_{v},sum_{v}=sum_{u}(dp_{v}<dp_{u}+w_{v}) \\ sum_{v}=sum_{v}+sum_{u}(dp_{v}==dp{u}+w_{v}) \\ \end{cases} \]

很简单对吧。不多说了，上代码：

代码

P2272

#include<bits/stdc++.h>
#define int long long
#define mkp make_pair
using namespace std;

inline int read(){
	int x=0,f=1;char c=getchar();
	while(c<48){
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}

inline void write(int x){
	if(x<0) putchar('-'),x=-x;
	if(x<10) putchar(x+'0');
	else write(x/10),putchar(x%10+'0');
}

const int N=1e5+5;
const int M=1e6+6;
int n,m,mod,h[N],nh[N],ntot,tot,newn,at[N];
//nh[],ntot:存新图的
//newn:新图的点的个数
//at[i]:旧图中的i在新图的哪个点里 
int dfn[N],low[N],awa,vis[N];
//awa:Tarjan中的时间戳，至于为啥是awa，因为比较可爱 
int w[N],dp[N],sum[N],in[N];
//w[i]:新图中i的点权（即它里面有多少原图里的点）
//dp[],sum[]:同题解 
map<pair<int,int> ,bool> mp;
//mp:判重边的 
stack<int> st;
queue<int> q;
struct sw{
	int u,v,nxt;
}e[2*M],ne[2*M]; 

inline void add(int u,int v){
	e[++tot]={u,v,h[u]};h[u]=tot;
}

inline void nadd(int u,int v){
	ne[++ntot]={u,v,nh[u]};nh[u]=ntot;in[v]++;
}

inline void tar(int u){//Tarjan
	dfn[u]=low[u]=++awa;
	vis[u]=1;
	st.push(u);
	for(int i=h[u];i;i=e[i].nxt){
		int v=e[i].v;
		if(!dfn[v]){
			tar(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]){
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(dfn[u]==low[u]){//缩点，不会的移步P3387 
		int owo=0;newn++;
		do{
			owo=st.top();st.pop();
			vis[owo]=0;at[owo]=newn;w[newn]++;
		}while(owo!=u);
	}
}

signed main(){
	n=read(),m=read(),mod=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read();
		add(u,v);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			tar(i);
		}
	}
	for(int i=1;i<=newn;i++){
		vis[i]=0;
	}
	for(int i=1;i<=tot;i++){
		int u=e[i].u,v=e[i].v;
		int x=at[u],y=at[v];
		if(!mp[mkp(x,y)]&&at[u]!=at[v]){
			//一定要判好重边，否则最长路个数会重复计算 
			//以及，不要用并查集判重边。。。 
			nadd(x,y);
			mp[mkp(x,y)]=1;
		}
	}
	//topo
	for(int i=1;i<=newn;i++){
		if(!in[i]){
			q.push(i);dp[i]=w[i];sum[i]=1;vis[i]=1;
		}
	}
	while(!q.empty()){
		int u=q.front();q.pop();
		for(int i=nh[u];i;i=ne[i].nxt){
			int v=ne[i].v;
			if(vis[v]) continue;
			if(in[v]){
				in[v]--;
				if(dp[u]+w[v]>dp[v]){
					dp[v]=dp[u]+w[v];sum[v]=sum[u];
				}
				else if(dp[u]+w[v]==dp[v]){
					sum[v]=(sum[v]+sum[u])%mod;
				}
			}
			if(!in[v]){
				q.push(v);vis[v]=1;
			}
		}
	}
	//统计答案 
	int ans=0,CNT=0;
	for(int i=1;i<=newn;i++){
		if(dp[i]>ans){
			ans=dp[i];CNT=sum[i];
		}
		else if(dp[i]==ans){
			CNT=(CNT+sum[i])%mod;
		}
	}
	printf("%lld\n%lld",ans,CNT);
	return 0;
}

Tips

不要使用并查集判断重边。。。详情移步这个帖子。

如果你觉得这篇题解还不错的话，不妨点个赞吧qwq