P7915 [CSP-S 2021] 回文

题目传送门

首先题意这里有个理解误区：不是让最终形成的回文串的字典序最小，而是要让操作序列（即那串由L和R构成的序列）字典序最小。换言之，要在保证方案存在的情况下尽可能使用L操作。

首先我们先考虑将最左侧数字首先拿出来的情况（先拿最右边那个数同理）：

以第一个样例为例：

5
4 1 2 4 5 3 1 2 3 5

将最左侧的4拿出后，为了保证最后\(b\)数组回文，我们需要保证中间的4最后一个被拿走，即在此之前都只能从它两侧的最顶端拿数。

如下图所示，这样的话中间的4两边就分别形成了一个栈：

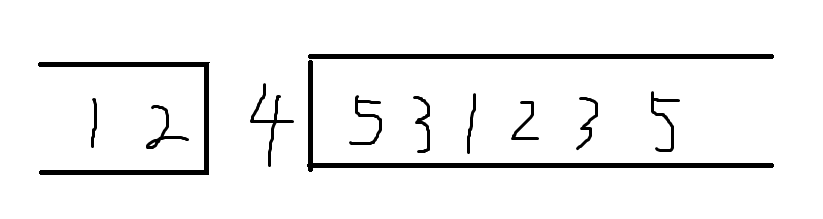
接下来我们考虑完了首尾元素，该考虑第二位及倒数第二位了。这两位很显然，是仅次于首尾元素里最早第一次出栈，最晚第二次出栈的。

要做到在未考虑的元素里最早出栈，说明这一位的元素的两个值，有一个在栈顶；同理，最晚第二次出栈，说明另一个值在栈底。

这样一来，第二及倒数第二个位置的数就要一个在栈底、一个在栈顶。就比如样例，满足条件的只有5一个数，说明第二位的数就是5。

既然这一位考虑完了，我们就把5从所在栈底栈顶出栈，把两个值都出掉。

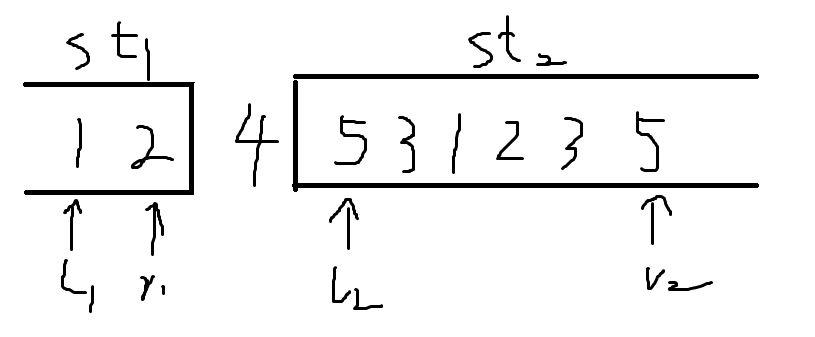
（注：\(l1,r1,l2,r2\)分别为两个栈\(st1,st2\)的栈顶栈底指针，实际上这两个栈更类似于双端队列……）

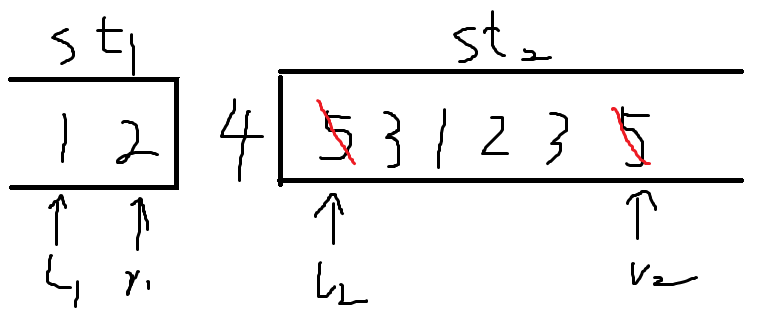
然后就是第三个位置。同第二个位置，只有同时存在于栈顶和栈底的元素才能填充位置，样例里也就是3。然后我们删掉两个3。

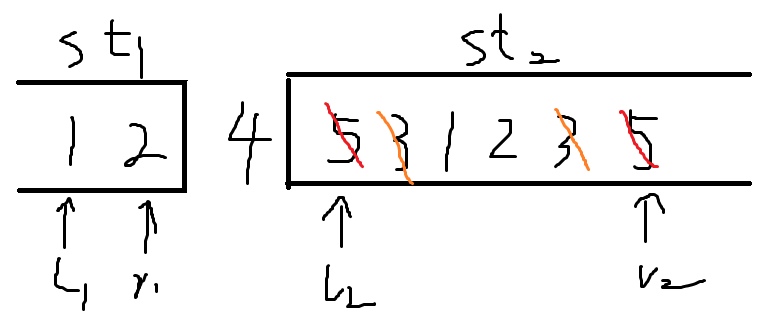
以此类推，如果这个位置能填充一个合法的数字，当且仅当它同时出现在某个栈的栈顶或栈底。显然，满足这条性质的数至多只有两个。

无论是两个数同时出现在同一个栈的栈顶、栈底，或是在两个栈的栈顶和栈底皆可，因为我们只需要让它之前和之后都没有要出栈的待定位置的元素。

那如果有两种这样的数，我们优先将左侧栈顶的数出栈，因为左侧数出栈的命令是"L"，字典序比将右侧数出栈的命令"R"小。

就比如接下来第四个位置，1和2都满足性质，但是为了让结果字典序最小，我们将1出栈。

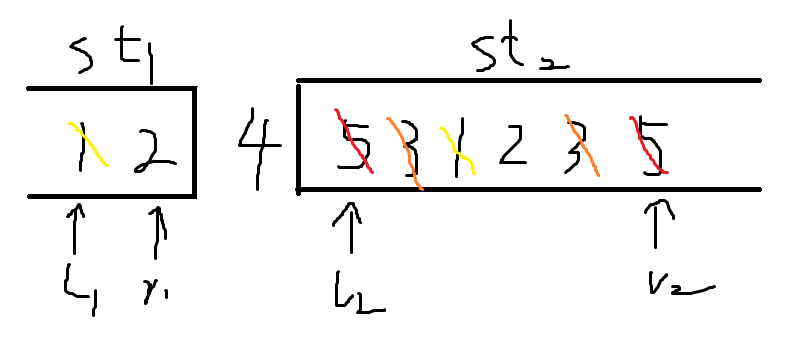
轮到第五位，我们将2出栈。

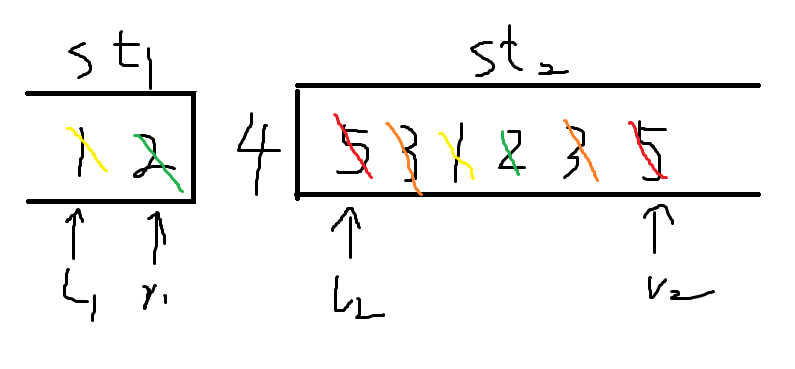
这样最小的操作序列就诞生了。

如果说找不到这样的数，比如第二个样例，说明该情况不可行。

如果第一次操作取"L"找不到解，我们将第一次操作取"R"再跑一遍，如果还是不行就直接输出-1。

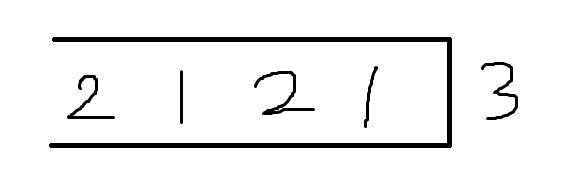
这样这个题\(O(n)\)算法的思路就有了，具体实现还要注意一点，就是务必检查好你的循环/判断/数组大小理论上应该是\(n\)还是\(2n\)。。。很容易就被这个卡出很多奇奇怪怪的错误。。。

代码：

P7915

#include<bits/stdc++.h>
#define int long long
using namespace std;

inline int read(){
	int x=0,f=1;char c=getchar();
	while(c<48){
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}

const int N=5e5+5;
int T,n,a[2*N],st1[2*N],st2[2*N],l1=1,r1=0,l2=1,r2=0,ans[2*N];
//ans[i]:为0则第i次操作为L,否则为R 

signed main(){
	T=read();
	while(T--){
		n=read();
		int pos1=0,pos2=0;
		
		for(int i=1;i<=2*n;i++){
			ans[i]=0;
		}
		l1=l2=1;r1=r2=0;
		//st1,st2,l1,r1,l2,r2同题解
		//pos1,pos2:pos1存储a[1]的另一个位置，pos2存储a[2*n]的另一个位置 
		
		for(int i=1;i<=2*n;i++){
			a[i]=read();
			if(a[i]==a[1]&&i!=1){
				pos1=i;
			}
		}
		for(int i=2*n-1;i>=1;i--){
			if(a[i]==a[2*n]){
				pos2=i;
			}
		}
		//st1,st2初始化（第一次操作为L） 
		for(int i=2;i<pos1;i++){
			st1[++r1]=a[i];
		}
		for(int i=pos1+1;i<=2*n;i++){
			st2[++r2]=a[i];
		}
		int fl=1,tot=0;
		ans[++tot]=0;ans[2*n+1-tot]=0;
		while(fl){
			//合法的数只有4种情况：
			//1.两个数同时在st1的栈顶和栈底，令l1++ r1--使两个数出栈。 
			//这种情况对应到原操作序列是两个对应的L。 
			//2.两个数同时在st1的栈顶和st2的栈底，令l1++ l2++使两个数出栈。 
			//这种情况对应到原操作序列是一个L和一个R。 
			//3.两个数同时在st2的栈顶和st1的栈底，令r1-- r2--使两个数出栈。 
			//这种情况对应到原操作序列是一个R和一个L。 
			//4.两个数同时在st2的栈顶和栈底，令l2++ r2--使两个数出栈。 
			//这种情况对应到原操作序列是两个对应的R。
			//注意，23两种情况要判断两个栈都非空，14只需要判断对应的栈非空，但是对应的栈里至少要剩两个数  
			if(l1<r1&&st1[l1]==st1[r1]){
				ans[++tot]=0;l1++;r1--;
				ans[2*n+1-tot]=0;
			}
			else if(l1<=r1&&l2<=r2&&st1[l1]==st2[l2]){
				ans[++tot]=0;l1++;l2++;
				ans[2*n+1-tot]=1;
			}
			else if(l1<=r1&&l2<=r2&&st1[r1]==st2[r2]){
				ans[++tot]=1;r1--;r2--;
				ans[2*n+1-tot]=0;
			}
			else if(l2<r2&&st2[l2]==st2[r2]){
				ans[++tot]=1;l2++;r2--;
				ans[2*n+1-tot]=1;
			}
			else{
				fl=0;//找不到这样的数就没法往下找了 
			}
		}
		//我们用tot里存了几次操作判断是否可行，如果tot==n则说明可行，否则不可行 
		if(tot>=n){
			for(int i=1;i<=2*n;i++){
				if(ans[i]){
					cout<<"R";
				}
				else{
					cout<<"L";
				}
			}
			cout<<endl;
		}
		else{//第一次操作为L不可行，让第一次操作为R
			//注意重新初始化 
			l1=1;r1=0;l2=1;r2=0;
			for(int i=1;i<pos2;i++){
				st1[++r1]=a[i];
			}
			for(int i=pos2+1;i<2*n;i++){
				st2[++r2]=a[i];
			}
			fl=1,tot=0;
			ans[++tot]=1;ans[2*n+1-tot]=0;
			while(fl){
				if(l1<r1&&st1[l1]==st1[r1]){
					ans[++tot]=0;l1++;r1--;
					ans[2*n+1-tot]=0;
				}
				else if(l1<=r1&&l2<=r2&&st1[l1]==st2[l2]){
					ans[++tot]=0;l1++;l2++;
					ans[2*n+1-tot]=1;
				}
				else if(l1<=r1&&l2<=r2&&st1[r1]==st2[r2]){
					ans[++tot]=1;r1--;r2--;
					ans[2*n+1-tot]=0;
				}
				else if(l2<r2&&st2[l2]==st2[r2]){
					ans[++tot]=1;l2++;r2--;
					ans[2*n+1-tot]=1;
				}
				else{
					fl=0;
				}
			}
			if(tot<n){//无解 
				printf("-1\n");
			}
			else{//第一次操作为R有解 
				for(int i=1;i<=2*n;i++){
					if(ans[i]){
						cout<<"R";
					}
					else{
						cout<<"L";
					}
				}
				cout<<endl;
			}
		}
	}
	return 0;
}