哈希
update&勘误:不要写hs[i]=hs[i-1]*B+(s[i]-'a'),这样的话a和aa的哈希值就一样了,更容易哈希冲突。很抱歉之前的写法有误。
由于当时本人没有意识到这个问题,所以代码写的全部是错误写法,在此说明,代码不作改动。
哈希是一个很神奇的东西。那么这一块呢,给咱同学做个说明。
一.字符串哈希
把一个字符串映射到一个整数的函数称作哈希函数,映射到的这个整数就是这个字符串的哈希值。
一般采用多项式哈希函数求字符串哈希值,即
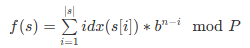

当然毕竟哈希是把大范围映射到小范围里,难免会有哈希冲突,即两个不同的字符串的哈希值相等。双哈希是个很好的解决方法,也就是算两套哈希值,只有两个哈希值都一样才会被判定为是同一字符串。
例1.P3370
字符串哈希的模板题,可以将字符串多项式哈希后比较哈希值是否相等,单哈希即可通过。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2025;
const int T=1e4+4;
const int B=13331;
const int mod=998244353;
int t,n,a[T];
char s[N];
int main(){
scanf("%d",&t);
for(int i=1;i<=t;i++){
scanf("%s",s+1);
n=strlen(s+1);
int HASH=0;
for(int j=1;j<=n;j++){
HASH=(HASH+(int)(s[j]))%mod;
HASH=(HASH*B)%mod;
}
a[i]=HASH;
}
sort(a+1,a+t+1);
int len=unique(a+1,a+t+1)-a-1;
printf("%d",len);
return 0;
}
例2.ABC398F
当年这个题的赛时数据实在太水了,暴力都能打过去,不过后来加强了,遂讲其哈希之做法。
题目求的是最短的以原字符串为前缀的回文串,可以转化为求最长的原字符串的后缀回文子串,而回文串不管是正着求哈希还是倒着求哈希,哈希值都是固定的,我们就用这个性质判断是否回文。
单哈希就能过,当然双哈希更保险。
单哈希
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int B=79;
const int mod=998244353;
const int N=5e5+5;
int lst,hs1,hs2,n,pw[N];
char c[N];
signed main(){
scanf("%s",c+1);
n=strlen(c+1);
pw[0]=1;
for(int i=1;i<=n;i++){
pw[i]=pw[i-1]*B%mod;
}
for(int i=n;i;i--){
hs1=(hs1*B+(int)(c[i]))%mod;
hs2=(hs2+(int)(c[i])*pw[n-i])%mod;
//cout<<"i="<<i<<endl;
//cout<<hs1<<" "<<hs2<<endl;
if(hs1==hs2){
lst=i;
}
}
for(int i=1;i<lst;i++){
cout<<c[i];
}
for(int i=n;i;i--){
cout<<c[i];
}
return 0;
}
双哈希
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int B1=79;
const int mod1=998244353;
const int B2=233;
const int mod2=1e9+7;
const int N=5e5+5;
int lst,hs1,hs2,hs3,hs4,n,pw1[N],pw2[N];
char c[N];
signed main(){
scanf("%s",c+1);
n=strlen(c+1);
pw1[0]=pw2[0]=1;
for(int i=1;i<=n;i++){
pw1[i]=pw1[i-1]*B1%mod1;
pw2[i]=pw2[i-1]*B2%mod2;
}
for(int i=n;i;i--){
hs1=(hs1*B1+(int)(c[i]))%mod1;
hs2=(hs2+(int)(c[i])*pw1[n-i])%mod1;
hs3=(hs3*B2+(int)(c[i]))%mod2;
hs4=(hs4+(int)(c[i])*pw2[n-i])%mod2;
//cout<<"i="<<i<<endl;
//cout<<hs1<<" "<<hs2<<endl;
if(hs1==hs2&&hs3==hs4){
lst=i;
}
}
for(int i=1;i<lst;i++){
cout<<c[i];
}
for(int i=n;i;i--){
cout<<c[i];
}
return 0;
}
----------------------------------------------------------并不华丽的分割线----------------------------------------------------------
很多字符串的算法也可以用哈希暴力解决,比如manache和KMP。
例3.P3375&P4824
本来是两个KMP的题目的,但是如果考场上忘了怎么写———哈希,启动!
KMP模板题可以用哈希做第一问,但第二问用哈希做就不太行,所以只放第一问核心代码。
核心代码
for(int i=1;i<=n2;i++){//由于第二个串只需要完整哈希值,所以不用开数组
hs2=((hs2*B)%mod+(s2[i]-'A')%mod)%mod;
}
for(int i=1;i<=n1;i++){
hs1[i]=((hs1[i-1]*B)%mod+(s1[i]-'A')%mod)%mod;
if(hs1[i]-hs1[i-n2]*pw[n2]==hs2){//判断两串是否相等
printf("%d\n",i-n2+1);
}
}
P4824的一般做法是把原串按顺序丢进栈中,同时用KMP进行匹配,栈首匹配成功就将匹配部分弹出栈,最后剩下的就是答案。具体可参考前几篇题解。
但是有一般就会有二般。
如果你一不小心忘了KMP怎么写时,今天的主角哈希就登场了。
同样是把字符串扔进栈里,不过用哈希代替KMP匹配,匹配成功就把匹配部分弹出,和刚才基本类似。
P4824完整代码
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;//自然溢出就相当于取模了,起码不会有负数
const int N=1e6+6;//更正,其实是屑作者没判边界
const ull B=131;
int n1,n2,top;
ull hs2,pw[N],hst[N];
char s1[N],s2[N],st[N];
signed main(){
scanf("%s%s",s1+1,s2+1);
n1=strlen(s1+1),n2=strlen(s2+1);
/*
if(n1<n2){
//要删除的串比原串还长,那就不会有要删的子串了
printf("%s",s1+1);
return 0;
}
*/
pw[0]=1;
for(int i=1;i<=n2;i++){
pw[i]=pw[i-1]*B;
hs2=((hs2*B)+(s2[i]-'a'));
}
for(int i=1;i<=n1;i++){
st[++top]=s1[i];//入栈
hst[top]=((hst[top-1]*B)+(s1[i]-'a'));
if(top<n2){//如果栈里不足n2个元素是肯定不会匹配成功的,不判会RE
continue;
}
if(hs2==hst[top]-hst[top-n2]*pw[n2]){//匹配成功
top-=n2;//就把这一段出栈,注意这里不会影响前面字符串,所以前面的哈希值不用改
}
}
for(int i=1;i<=top;i++){
cout<<st[i];
}
return 0;
}
例4.P3805
本来是manache的经典板子题,但是如果你又一不小心把manache忘了 (那很不小心了)
那么哈希也能过掉这个题。
和马拉车有点类似,我们枚举中间点i,分奇数个字母的回文串和偶数个字母(此时i为偏左的那个点)的回文串两种情况讨论。
设len为回文串的半径(含端点),那么如果len+1回文len就回文,len-1不回文len就不回文,所以可以用O(nlogn)的时间复杂度解决。(可以过,就是时间很紧张)
但是,既然求最长回文串,那就没必要先二分,把当前的最优答案ans记录下来,并且判断以i为中心点、以ans为基础能否延展,可以的话就更新答案ans。
这样时间复杂度就差不多是O(n)了,虽然和manacher差点,但也足够AC了。
P3805哈希
#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
const int N=1.1e7+1;
const ull B=131;
int n,ans;
ull hs1[N],hs2[N],pw[N];
char s[N];
int main(){
scanf("%s",s+1);
n=strlen(s+1);
//for(int i=1;i<=n;i++){
// cout<<s[i];
//}
//cout<<endl;
pw[0]=1;
for(int i=1;i<=n;i++){
pw[i]=pw[i-1]*B;
}
for(int i=1;i<=n;i++){
hs1[i]=hs1[i-1]*B+(int)(s[i]);//正着求
hs2[n-i+1]=hs2[n-i+2]*B+(int)(s[n-i+1]);//倒着求
}
for(int i=1;i<=n;i++){
int len=(ans+1)>>1;//在最优答案的基础上判断能否更优
int l=i-len,r=i+len;
//判断回文的方法同ABC398F
while(l>=1&&r<=n&&hs1[r]-hs1[l-1]*pw[r-l+1]==hs2[l]-hs2[r+1]*pw[r-l+1]){//奇
len++;ans=max(ans,2*len-1);l--;r++;//若可以就更新
}
len=ans>>1;
l=i-len,r=i+len+1;
while(l>=1&&r<=n&&hs1[r]-hs1[l-1]*pw[r-l+1]==hs2[l]-hs2[r+1]*pw[r-l+1]){//偶
len++;ans=max(ans,2*len);l--;r++;
}
}
printf("%d",ans);
return 0;
}
值得一提的是,其实我们可以像马拉车一样在字符中间插入井号,这样就不用判断是奇数个还是偶数个字母的回文串了。
不过这个题显然不太行,数组占空间8.8e7,大抵会MLE。
例5.P3763
刚才我们反复提到哈希的一个性质:对于两个字符串s1,s2,如果他们的前i位相同,则前i-1位一定相同;如果前i位不同,则前i+1位不同。
这也就决定了哈希可以和二分搭配使用,比如这个题。
根据上述性质,我们可以三次二分,具体地说,每次二分求s1,s2的最大匹配长度l,则第l+1位一定失配。接着我们跳过l+1位,从s1,s2剩余未匹配部分接着找最大匹配长度,以此类推,直到s2匹配完成或已经进行了3次二分。
注意,如果是后一种情况的话,那三次二分完成后需要检验剩余部分是否相同。以及,多组数据一定记得清空+初始化。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N=1e5+5;
const int B=131;
int T,n1,n2,ans;
ull pw[N],hs1[N],hs2[N];
char s1[N],s2[N];
ull HASH(ull hs[],int l,int r){
return hs[r]-hs[l-1]*pw[r-l+1];
}
bool check(int x){
int l1=x,l2=1,r1=x+n2-1,r2=n2,lst=0;
//lst:已经匹配了多少位
for(int t=1;t<=3;t++){
int l=0,r=n2-lst,mid;//二分两串可以匹配的最大长度
//最差一个都匹配不上,最好剩下的都能匹配上
while(l<r){
mid=(l+r+1)>>1;
if(HASH(hs1,l1,l1+mid-1)==HASH(hs2,l2,l2+mid-1)){//能匹配上
l=mid;//就向后取mid,当然这个位置要保留
}
else{//匹配不上
r=mid-1;
}
}
//cout<<"l="<<l<<endl;
l1=l1+l+1;l2=l2+l+1;
lst+=l+1;
//注意要跳过失配位置
if(l2>r2){//已经匹配完了
return 1;
}
}
return (HASH(hs1,l1,r1)==HASH(hs2,l2,r2));
//此时已经有3位失配,需要判断剩下的串是否相同
}
int main(){
scanf("%d",&T);
pw[0]=1;
while(T--){
ans=0;//从0->100只需要一个清空
scanf("%s%s",s1+1,s2+1);
n1=strlen(s1+1),n2=strlen(s2+1);
//初始化
for(int i=1;i<=n2;i++){
pw[i]=pw[i-1]*B;
}
for(int i=1;i<=n1;i++){
hs1[i]=hs1[i-1]*B+s1[i];
}
for(int i=1;i<=n2;i++){
hs2[i]=hs2[i-1]*B+s2[i];
}
for(int i=1;i+n2-1<=n1;i++){//枚举可能是基因开头位置的i
//cout<<"i="<<i<<endl;
if(check(i)){
ans++;
}
}
printf("%d\n",ans);
}
return 0;
}
课后复习题:P4503
二.哈希表
哈希表是一种通过计算键的哈希值,并使用该哈希值作为数组的索引来存储和检索键值对的数据结构。常用的映射函数是将原数取模存储到数组中。
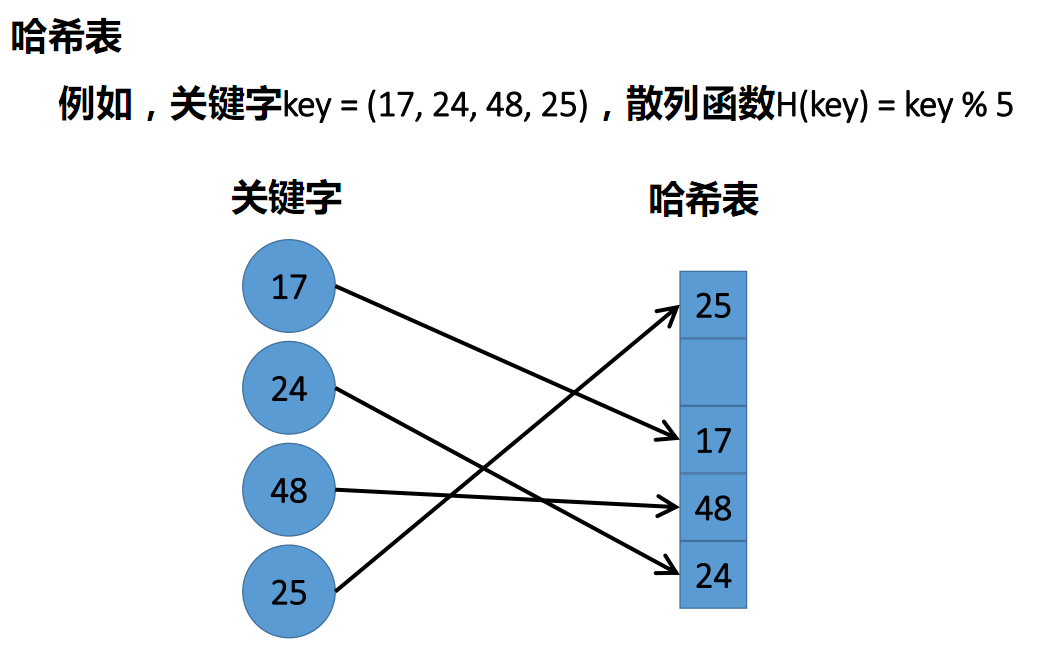
但是哈希毕竟是将大范围的数映射到小范围内,难免会有冲突。这个时候,一般会采用常见的两种方法处理。
第一种是开放定址法,即向前找下一个空着的位置并存数,包括线性探测(一次只走一步)和二次探测(步长为平方)等。
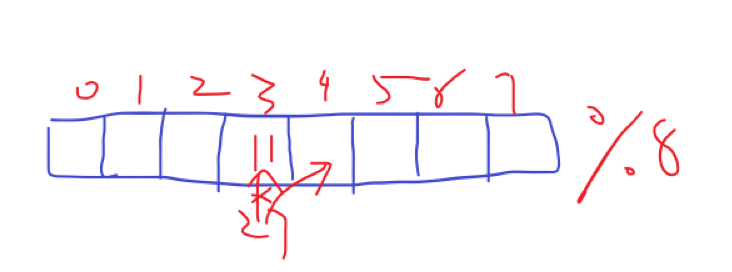
缺点是可能发生较连续的冲突
第二种是链表法,将多个冲突的数放在一个纵向链表里,如图。
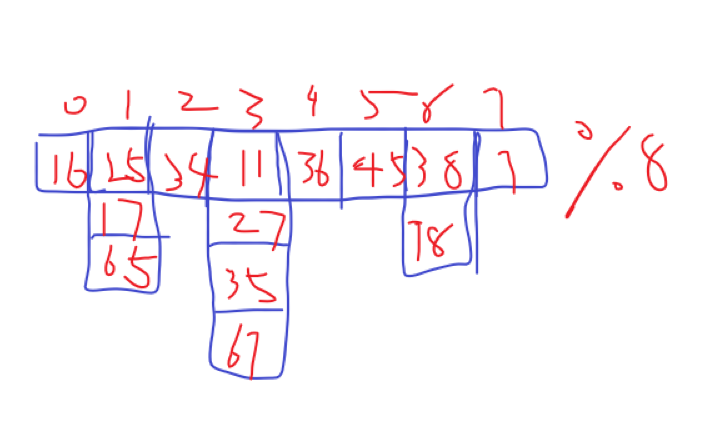
缺点是如果冲突集中查找复杂度会退化为O(n)。
例1.P11615
哈希表板子题。
介于这个题开unordered_map等其他数据结构会被卡,所以我们采用手写哈希表。
这里我用的是vector模拟哈希链表,而且开了pair,其中x表示映射前的数,y表示映射后的数。
每次查找x位时就先找到x所在的哈希表下标(这里是x%mod=mm),然后遍历mm里所有元素,找到了就收工,找不到说明x原来不在哈希表里,就在mm里新建一个x的位置。
这个题要求对2^64取模,但其实用ull自然溢出就约等于取模了。
点击查看代码
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef unsigned long long ull;
const int N=5e6+6;
const int mod=1e7+19;//某位大佬给的哈希表建议:约2~3倍元素个数N大小的质数
ull n;
//题目给的快读,听说不用会TLE
//输入出现读入n及n对数后可继续输入的问题时,试试ctrl+Z
char buf[1<<23],*p1=buf,*p2=buf;
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
inline unsigned long long rd() {//读入一个 64 位无符号整数
unsigned long long x=0;
char ch=gc();
while(!isdigit(ch))ch=gc();
while(isdigit(ch)) x=x*10+(ch^48),ch=gc();
return x;
}
vector<pair<ull,ull> > h[mod+5];
void CHANGE(ull x,ull y){//改变y值
ull mm=x%mod;
for(ull i=0;i<h[mm].size();i++){
if(h[mm][i].x==x){//查询、更改
h[mm][i].y=y;
break;
}
}
}
ull FIND(ull x){//查找函数
ull mm=x%mod;
for(ull i=0;i<h[mm].size();i++){
if(h[mm][i].x==x){
return h[mm][i].y;//找到直接返回
}
}
h[mm].push_back((pair<ull,ull>){x,0});//找不到则说明原来没有,新建一个空位
//注意这里的大部分变量都得开ull
return 0;
}
int main(){
n=rd();
ull sum=0;
for(ull i=1;i<=n;i++){
ull x=rd();ull y=rd();
ull ans=FIND(x);
CHANGE(x,y);
sum=sum+i*ans*1ll;
}
cout<<sum;
return 0;
}
三.其他哈希
详情请见这个题单。
包括但不限于哈希+线段树、树哈希。 作者是蒟蒻,所以这里不展开讲了
参考资料:
1.哈希题单
2.大佬的哈希文章
3.洛谷题解P4824
4.洛谷题解P3763
5.洛谷题解P11615


 浙公网安备 33010602011771号
浙公网安备 33010602011771号