CF1363C Game On Leaves(简单博弈）

CF1363C Game On Leaves

题意：

给定 \(n\) 个节点的无根树。

两名选手轮流操作，每次可以选择一个叶节点并删除它以及所有和它相连的边。叶节点指度数不超过 \(1\) 的节点。删除节点 \(x\) 的选手胜利。

你需要判断先手是否有必胜策略。具体来讲，如果先手有必胜策略，输出 \(Ayush\)，否则输出 \(Ashish\)。

多组数据，数据组数 \(t \leq 10\)，\(n \leq 1000\)。

思路：

分类讨论：

• \(x\)是叶子节点，则先手赢。
• \(n=1\)，则先手赢。
• \(n-3\)是偶数，则先手输。
• \(n-3\)是奇数，则先手赢。

关于后面两个讨论的简单证明：

易得知，此时\(x\)不是叶子，选\(x\)为树根重构这棵树。

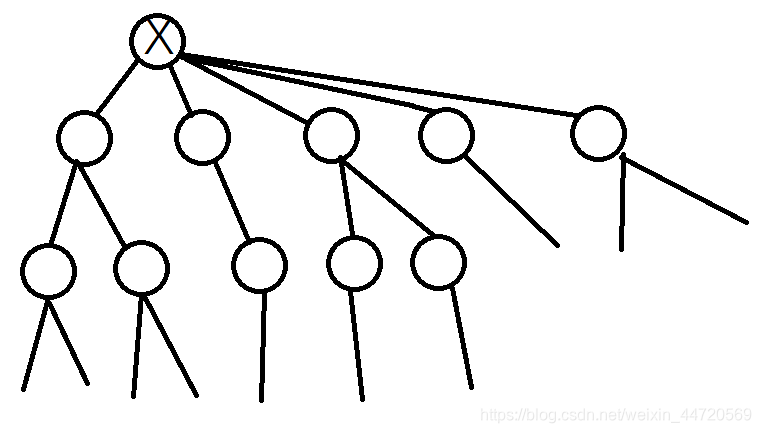
按规则，考虑把所有叶子节点不断删除，直到\(x\)的每个子树只剩一个节点时，如下。

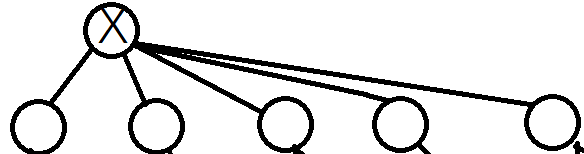
由图可观察到，还可以继续删除\(x\)的儿子节点。

于是不难想到，以\(x\)为根的游戏的最终状态一定以\(x\)只有两个儿子节点的形式呈现，因为其他点在不同的时间点都会做为叶子节点删去。
最终状态：

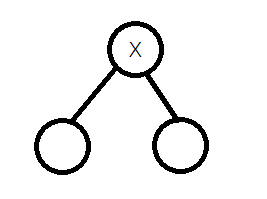
所以\(n-3\)即表示删去的点数。

• 若\(n-3\)是偶数，则到最终状态时，轮到先手取叶子，取完后另一个人取\(x\)，则为后手获胜。
• 若\(n-3\)是奇数，则到最终状态时，轮到后手取叶子，取完后另一个人取\(x\)，则为先手获胜。

证毕

Code：

#include<bits/stdc++.h>
using namespace std;
int d[3000];
/**
 * 简单博弈
 * @return [description]
 */
int main(){
	int n,x;
	int t;
	cin>>t;
	while(t--){
		cin>>n>>x;
		int l,r;
		for(int i=1;i<=n-1;++i)d[i]=0;
		for(int i=1;i<=n-1;++i){
			cin>>l>>r;
			d[l]++;
			d[r]++;
		}
		if(n==1){
			puts("Ayush");

		}
		else if(d[x]==1){
			puts("Ayush");
		}
		else if((n-3)%2==0){
			puts("Ashish");
		}
		else puts("Ayush");
	}
	return 0;
}