单调栈与单调队列专题

这是栈和队列的一个高级应用，需要重点掌握，可以从LeetCode中看出来，这类型的题大多数都是Hard级别，面试中出现的频率也是属于比较高的

---

单调栈

这是一道典型的单调栈的问题，显然，我们需要维持一个递增栈

class Solution {
    public int[] nextLargerNodes(ListNode head) {
        List<Integer> list = new ArrayList<>();
        for(ListNode fakehead = head; fakehead != null; fakehead = fakehead.next){
            boolean flag = false;
            int t = Integer.MAX_VALUE;
            for(ListNode nexts = fakehead.next; nexts != null; nexts = nexts.next){
                if(nexts.val > fakehead.val){
                    flag = true;
                    t = Math.min(t, nexts.val);
                }
            }
            if(!flag) list.add(0);
            else list.add(t);
        }
        int[] res = new int[list.size()];
            for(int i = 0; i<list.size(); i++)
                res[i] = list.get(i);
        return res;
    }
}

---

接下来看一道类似的题目，同样也是 Middle

先列出代码：

class Solution {
    public int[] dailyTemperatures(int[] T) {
        int[] res = new int[T.length];
        Stack<Integer> stack = new Stack<>();
        for(int i = 0; i<T.length; i++){
            int value = T[i];
            while(!stack.isEmpty() && value > T[stack.peek()]){
                int idx = stack.pop();
                res[idx] = i-idx;
            }
            stack.push(i);
        }
        return res;
    }
}

我们可以看出来，这两道题套路基本很相似，都是用Stack 存储索引，当不满足单调的条件，就开始出栈处理这些索引

---

可能你觉得上面的都简单嘛，接下来我们来解决几道Hard类型的题目，走起~

仔细观察，可以发现其实，就是一个单调栈的变种，隐藏比较深，我们可以这么想，这就是简单的木桶效应，最短的那根木头，决定木桶能装多少水，长度为6的那个最长的柱子，它不能单独决定最大的面积，往往还要考虑它周围比它短的柱子

class Solution {
    public int largestRectangleArea(int[] heights) {
        if(heights.length == 0) return 0;
        int[] left = new int[heights.length];
        int[] right = new int[heights.length];
        Stack<Integer> stack = new Stack<>();
        for(int i = 0; i<heights.length; i++){
            int v = heights[i];
            while(!stack.isEmpty() && v < heights[stack.peek()]){
                int idx = stack.pop();
                right[idx] = i;
            }
            stack.push(i);
        }
        while(!stack.isEmpty()) right[stack.pop()] = heights.length;
        for(int j = heights.length-1; j>=0; j--){
            int v = heights[j];
            while(!stack.isEmpty() && v < heights[stack.peek()]){
                int idx = stack.pop();
                left[idx] = j;
            }
            stack.push(j);
        }
        while(!stack.isEmpty()) left[stack.pop()] = -1;
        int res = -1;
        int v;
        for(int i = 0; i<heights.length; i++){
            v = (right[i]-left[i]-1)*heights[i];
            res = Math.max(res, v);
        }
        return res ;
    }
}

代码的思路是：针对每一根柱子，我们先从左往右计算右边第一根比它小的柱子，记录索引保存，从左往右记录左边第一根比它小的柱子的索引，以这个柱子为中心的最大面积就是 柱子的长度 * (右索引-左索引-1)，最后记录每根柱子为中心的面积，保存最大的那个面积， 即为我们的解。

---

其实，把上面那题Ac了，这题基本就没啥问题了，仔细瞅瞅，是不是稍微改下代码就是这题的题解了

class Solution {
    public int maximalRectangle(char[][] matrix) {
        int len = matrix.length;
        if(len == 0) return 0;
        int wid = matrix[0].length;
        if(wid == 0) return 0;
        int[] heights = new int[wid];
        int res = -1;
        for(int i = 0; i<matrix.length; i++){
            for(int j = 0; j<matrix[i].length; j++){
                if(matrix[i][j] != '0')
                heights[j] += 1;
                else
                heights[j] = 0;
            }
            res = Math.max(res, largestRectangleArea(heights));
        }
        return res;
    }

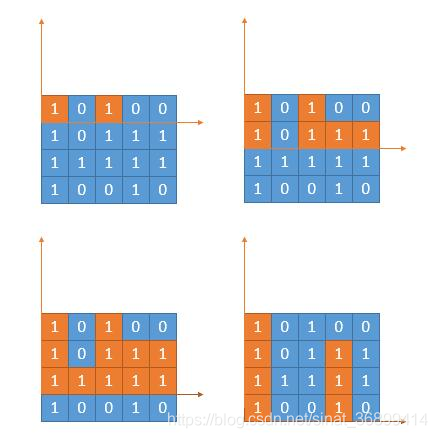
矩形的每一行，其实就是上一题求解矩形面积最大值，如下图所示：

---

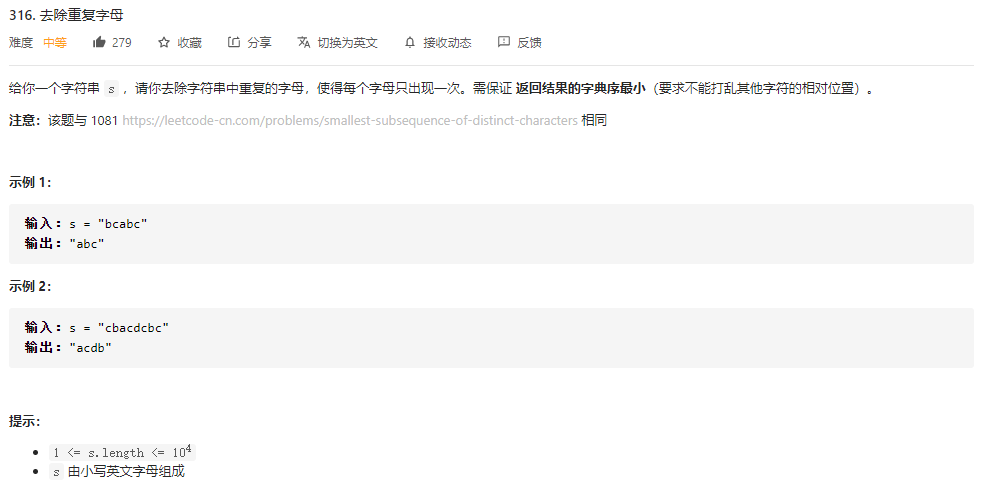
补充一道单调栈的题目 ----2020/11/24 ------ 做完这道题，再去试一下1081，同样也是差不多的题型

class Solution {
    public String removeDuplicateLetters(String s) {
        int len = s.length();
        if(len == 0) return s;
        char[] count = new char[26];
        for(char ch: s.toCharArray()) count[ch-'a'] ++;
        boolean[] instack = new boolean[26];
        Stack<Character> stack = new Stack<>();
        for(int i = 0; i<len; i++){
            char ch = s.charAt(i);
            count[ch-'a'] --;
            if(instack[ch-'a']) continue;
            while(!stack.isEmpty() && stack.peek() >= ch){
                if(count[stack.peek()-'a'] == 0) break;
                instack[stack.peek()-'a'] = false;
                stack.pop();
            }
            stack.push(ch);
            instack[ch-'a'] = true;
        }
        StringBuffer sb = new StringBuffer();
        while(!stack.isEmpty()) sb.append(stack.pop());
        return sb.reverse().toString();
    }
}

---

单调队列

这是一道典型的优先队列题目，求某个区间内的最大或者最小值，看完代码其实还是比较好理解：

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int len = nums.length;
        if(len <= 1) return nums;
        int[] res = new int[len-k+1];
        Deque<Integer> deque = new LinkedList<>();
        for(int i = 0; i<len; i++){
            while(!deque.isEmpty() && nums[i] > deque.peekLast()) deque.pollLast();
            deque.offerLast(nums[i]);
            if(i >= k-1){
                res[i-k+1] = deque.peekFirst();
                if(deque.peekFirst() == nums[i-k+1]) deque.pollFirst();
            }
        }
        return res;
    }
}

这类题目其实还有很多，在LeetCode中搜索标签，很多相关的例题，建议直接刷一遍。