论文阅读：比特币庞氏交易的检测

阅读报告：Data mining for detecting Bitcoin Ponzi schemes

论文简介：

比特币因为其匿名性的特征，被不法分子用来进行网络犯罪，包括诸如勒索，洗钱和庞氏骗局。本文就主要研究了如何通过机器学习算法来从比特币交易数据中识别庞氏骗局。庞氏骗局是一种是欺诈性投资，用后加入骗局的用户所投资的资金来偿还先前加入的用户，当不再能找到新的投资时，就会发生崩溃。

本文的主要内容是介绍了比特币交易的具体运作机制；搜集并公开了庞氏骗局的地址集合；提出了一组特征集合，来对每一笔交易进行描述，来作为后期分类的指标；提出了数据集检测存在两个类别不平衡的解决办法；进行试验找到效果最好的检测模型，即有监督的随即森林方法。

一、对比特币机制的介绍

首先，什么是比特币，我们可以把比特币和传统的金融机构进行对比：

传统的金融交易中，银行作为中心化的账本，我们的余额，交易活动，全部都经过银行系统的结算，记录。

对于比特币来说，区块链作为了一个去中心化的账本，大致的功能与中心化的银行类似。

 

比特币用户在电脑上运行比特币客户端软件，这样的电脑称为一个节点（node）。

大量节点电脑互相连接，形成一张像蜘蛛网一样的P2P（点对点）网络。

二、数据搜集

搜集的方法是再在bitcointalk.org用关键词“高收益 投资”搜索，且大多数网址需要在庞氏骗局网站注册才能获得相对应的转账地址。论文最终寻找到了32个的庞氏骗局转账地址。

三、地址聚类

由于比特币具有匿名性的特点，每个人可以为自己的钱包创建多个地址，因此从茫茫的地址数据中进行聚类，变为个体层面的分析很有必要。同时，地址聚类可以减少数据量，降低计算难度。

聚类的方法是，对于一个多输入交易，认为输入所使用的多个地址属于同一个用户。然后对所有的数据进行迭代，遍历所有地址数据进行聚类。

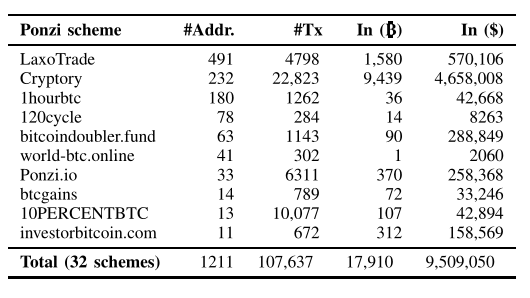
首先对庞氏骗局寻找到的32个地址进行以上方法聚类，得到了一些统计信息如下

Addr代表每个骗局聚类的地址数目，Tx代表交易数目，第三项代表涉及的流入金额，第四项代表流入金额转换为美元，使用交易当天的平均汇率。

 

四、特征划分

为了进行后续的机器学习算法，需要对每个地址提缺一些特征，作为算法的输入项。

•地址的生存期（表示单位是天）。根据地址第一个交易到最后一个交易之间的差计算得出。

•活动天数，指有交易发生的天数总和。

•地址的最大每日交易数。

•基尼系数，基尼系数代表财富不平等程度，0表示完全平等，而100表示​​完全不平等。

•传送到地址的所有值的总和。

•将钱转至地址（或从地址中转出）的交易数。

•转入交易和转出交易的比例。

•输入（或输出）交易值的平均值。

•短时间内互相交易的地址数量 。

•地址比特币到发送出比特币之间的最小（或最大，平均）延迟。

•连续两天的余额间的最大差额。

但是要注意的是，以上特征是针对地址定义的，而不是地址聚类，对于聚类来说，聚类的以上对应特征都是聚类内所有地址的特征组合。

五、实验数据集的构建

我们构建了一个包含两个类别的数据集:庞氏骗局(表示为P)和正常用户(表示为nP)。

数据集中的每个实体对应于一组比特币地址(即地址聚类)，它被表示为一组特征(即上节的特征，在最后加上类别标签P或nP)。

论文用庞氏骗局的32个实例和随机选择的6400个实例填充数据集（作为正常用户）。但是这其中存在两个类别比例极端的问题，虽然论文已经做到了1：200的比例，在实际的区块链环境中这个比例会更加极端。

对于类别不平衡问题，论文进行了如下处理：

在欺诈检测应用中，稀有类(即问题中的P类)的正确分类远比多数类(即nP类)的正确分类更重要，因为对欺诈案例进行错误分类的成本通常高于对合法案例进行错误分类的成本(因为后者可以通过事后分析来纠正)。论文中提出了两种处理这个问题的方法，包括基于抽样的方法和成本敏感的方法。

基于抽样的方法:基本思想是修改实例的分布，以便在用于模型开发的数据集中充分地表示少数类。最常见的采样技术是随机欠采样(RUS)，即从多数类中随机移除观察值。另一种方法是随机过采样(ROS)，将少数类的实例进行复制，但这可能导致过拟合

成本敏感的方法:成本敏感的学习涉及到成本矩阵的使用，它编码了类的实例错误的分类为另一个类的代价。即设置一个惩罚系数，论文中的做法是如果将庞氏骗局错误的分类成正常用户，将会受到比把正常用户分类为庞氏骗局更大的惩罚。

六、分类模型

6.1基于规则的分类

举一个例子感性上认识：

 

 

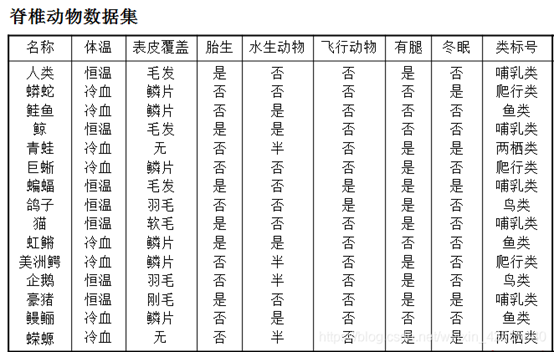
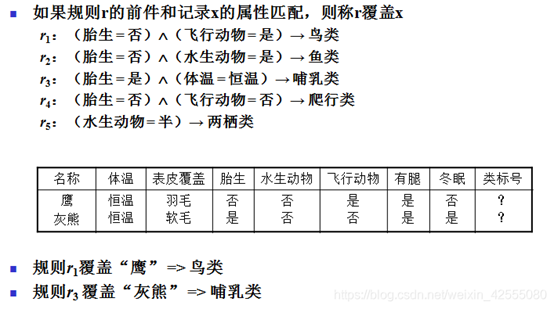
Rule: (条件1)^(条件2)....(条件n)-----> y

6.2贝叶斯分类：

首先了解一下条件概率的意义：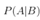

表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。

贝叶斯定理的意义是：我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。

 

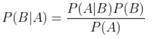
朴素贝叶斯分类的正式定义如下：

1、设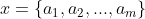为一个待分类项，而每个a为x的一个特征属性。

2、有类别集合。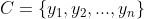

3、计算。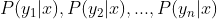

4、如果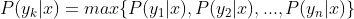，则。

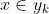那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：

1、找到一个已知分类的待分类项集合，这个集合叫做训练样本集。

2、统计得到在各类别下各个特征属性的条件概率估计。即

。

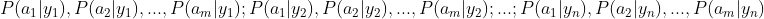3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

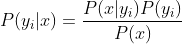
因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

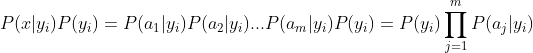
6.3随机森林：

决策树

 

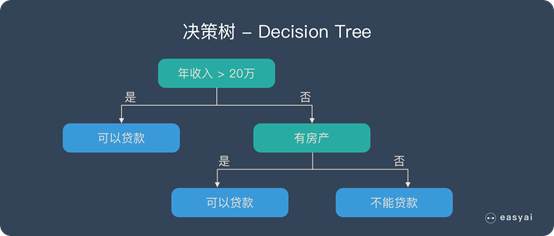
随机森林是由很多决策树构成的，不同决策树之间没有关联。

 

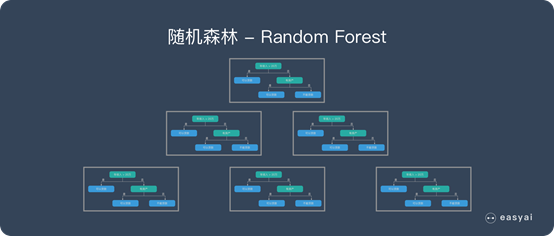
当我们进行分类任务时，新的输入样本进入，就让森林中的每一棵决策树分别进行判断和分类，每个决策树会得到一个自己的分类结果，决策树的分类结果中哪一个分类最多，那么随机森林就会把这个结果当做最终的结果。

构造随机森林的步骤：

一个样本容量为N的样本，有放回的抽取N次，每次抽取1个，最终形成了N个样本。这选择好了的N个样本用来训练一个决策树，作为决策树根节点处的样本。

当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。

决策树形成过程中每个节点都要按照步骤2来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了）。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。

按照步骤1~3建立大量的决策树，这样就构成了随机森林了

一个例子：

描述：根据已有的训练集已经生成了对应的随机森林，随机森林如何利用某一个人的年龄（Age）、性别（Gender）、教育情况（Highest Educational Qualification）、工作领域（Industry）以及住宅地（Residence）共5个字段来预测他的收入层次。

收入层次 :

Band 1 : Below $40,000

Band 2: $40,000 – 150,000

Band 3: More than $150,000

　　随机森林中每一棵树都可以看做是一棵CART（分类回归树），这里假设森林中有5棵CART树，总特征个数N=5，我们取m=1（这里假设每个CART树对应一个不同的特征）。

　　CART 1 : Variable Age

　　

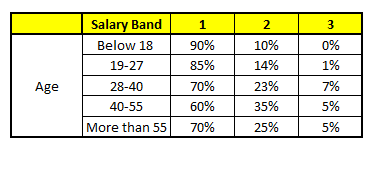
　　CART 2 : Variable Gender

　　

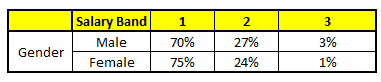
　　CART 3 : Variable Education

　　

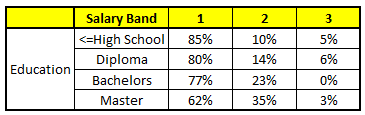
　　CART 4 : Variable Residence

　　

　　CART 5 : Variable Industry

　　

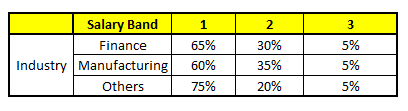
　　我们要预测的某个人的信息如下：

　　1. Age : 35 years ; 2. Gender : Male ; 3. Highest Educational Qualification : Diploma holder; 4. Industry : Manufacturing; 5. Residence : Metro.

　　根据这五棵CART树的分类结果，我们可以针对这个人的信息建立收入层次的分布情况：

　　

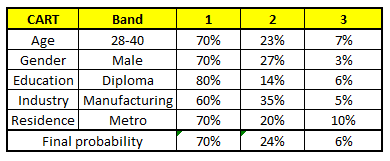
　　最后，我们得出结论，这个人的收入层次70%是一等，大约24%为二等，6%为三等，所以最终认定该人属于一等收入层次（小于$40,000）。

七、模型评价指标

在不平衡类分布的二元问题中，稀有类(P)被表示为正例，而多数类(nP)被表示为负例。

 

TP（True Positive）：模型预测为正例（1），实际为正例（1）的观察对象的数量。
TN（True Negative）：模型预测为负例（0），实际为负例（0）的观察对象的数量。
FP（False Positive）：模型预测为正例（1），实际为负例（0）的观察对象的数量。
FN（False Negative）：模型预测为负例（0），实际为正例（1）的观察对象的数量。

正确率（Accuracy）：指类被正确分类的概率

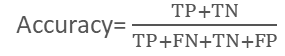
敏感度（Sensitivity）正例被正确分类的几率，也叫查全率（Recall）

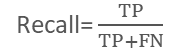
特异度（Specificity）负例被正确分类的几率

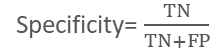
查准率（Precision）表示被预测为正例的实例中实际为正例的几率

查全率和查准率是一对矛盾的度量。一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。

在一些应用中，对查准率和查全率的重视程度有所不同。例如在商品推荐系统中，为了尽可能少打扰用户，更希望推荐内容确是用户感兴趣的，此时查准率更重要；而在逃犯信息检索系统中，更希望尽可能少的漏掉逃犯，此时查全率更重要。

F表示为两者的调和平均数

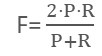
G表示为两者的几何平均数

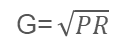
AUC是接收器操作特性(ROC)曲线下的区域，它显示了真阳性和假阳性率之间的权衡(模型越好，该区域越接近1)。

为了更好的测试分类器，实验使用了十折交叉验证

八、实验与结果

首先，未进行任何处理的实验，没有采用基于抽样和成本敏感的方法来降低类不平衡带来的影响。

结果如下，其中行索引指的是实际的类，而列索引指的是预测的类。可以看到，32个庞氏骗局都没有被完全识别。贝叶斯正确地分类了最大数量的庞氏骗局(32个中的23个)，但是误报(即，非庞氏骗局被分类为庞氏骗局)的数量也是最高的。这些结果证实，从高度不平衡的数据集分类是一项非常困难的任务。

第二步，使用随机抽样中的欠采样方法，具体而言，在交叉验证过程的每次迭代中，从多数类中随机移除实例，以减少类不平衡的程度:每200个非庞氏(1:200)实例中有1个庞氏的原始比例被减少到每40个非庞氏(1:40)实例中有1个庞氏，每20个非庞氏(1:20)实例中有1个庞氏，每10个非庞氏(1:10)实例中有1个庞氏，每5个非庞氏(1:5)实例中有1个庞氏。

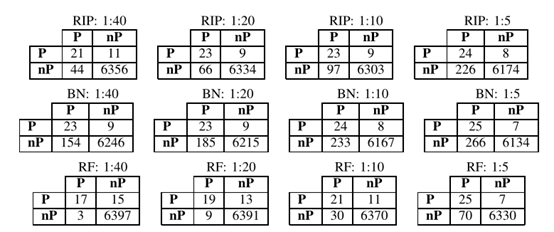
图3中的结果显示，欠采样方法提高了真阳性率。特别是，在1:5的设置下，随机森林识别的庞氏骗局数量与贝叶斯相同(32个中的25个)，但误报数量明显更少。贝叶斯产生了太多的误报(266)，甚至超过了RIPPER (226)。因此，虽然提高了真阳性率(影响查全率)，但欠采样方法在假阳性(影响查准率)方面并不令人满意。在查全率和查准率之间实现最佳平衡的困难是欺诈检测文献中公认的问题。

第三步，使用了成本敏感方法。在学习我们的检测模型时，我们使用下图的成本矩阵进行惩罚。

具来说，就是把庞氏骗局分类为非庞氏所付出的代价要远大于把非庞氏分类为庞氏。

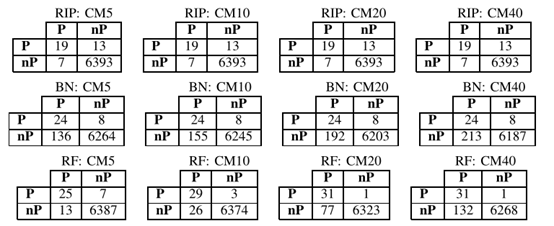
结果如图， RIPPER的结果和未进行处理时相同，这说明该算法对于惩罚正实例的错误分类不敏感。贝叶斯也没有特别明显的效果，这种方法错误分类仅仅减少一个，引起了假阳性的大幅度增加。

使用随机森林分类器可以获得最佳结果。当惩罚错误分类时，真阳性的数量增加(使用CM10的29和使用CM20的31)，错误分类大幅减少，虽然假阳性的数量依次增加，但是达到可以接受(分别为26和77)。特别的，进一步增加成本(CM40)是无益的，因为真阳性和错误分类的数量保持不变，但假阳性增加到132。

同时，还对成本敏感方法进行计算评价指标

就准确性而言，它简单地表示正确分类的实例的比例(不管它们的类别如何)，最好效果是CM5成本矩阵。同时它还确保最高的特异性和F分数（也就是查全率和准确率之间的平衡度最大）。

但是，在异常检测中，应该做到“宁杀一千，不漏一人”，更希望尽可能少的漏掉庞氏骗局，此时查全率更重要。在成本矩阵是CM20时，查全率效果最好，G分数也最好（表示了查全率和查准率的平衡），同时AUC值也是最高的。

考虑到这些因素，使用CM20获得的随机森林模型可以被认为是检测庞氏骗局最有效的方法。