层次分析法

层次分析法

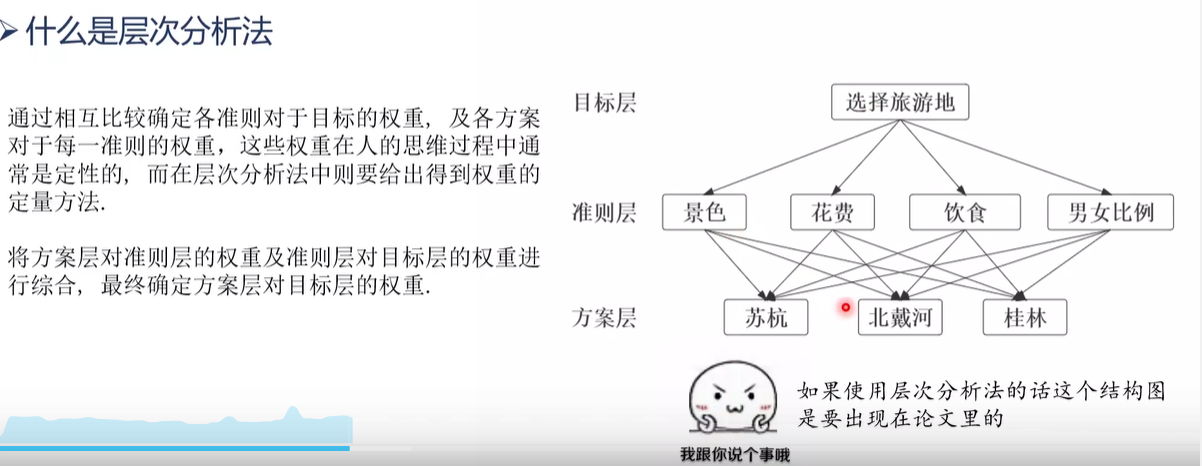
• 莫要忘记使用层次分析法要画结构图

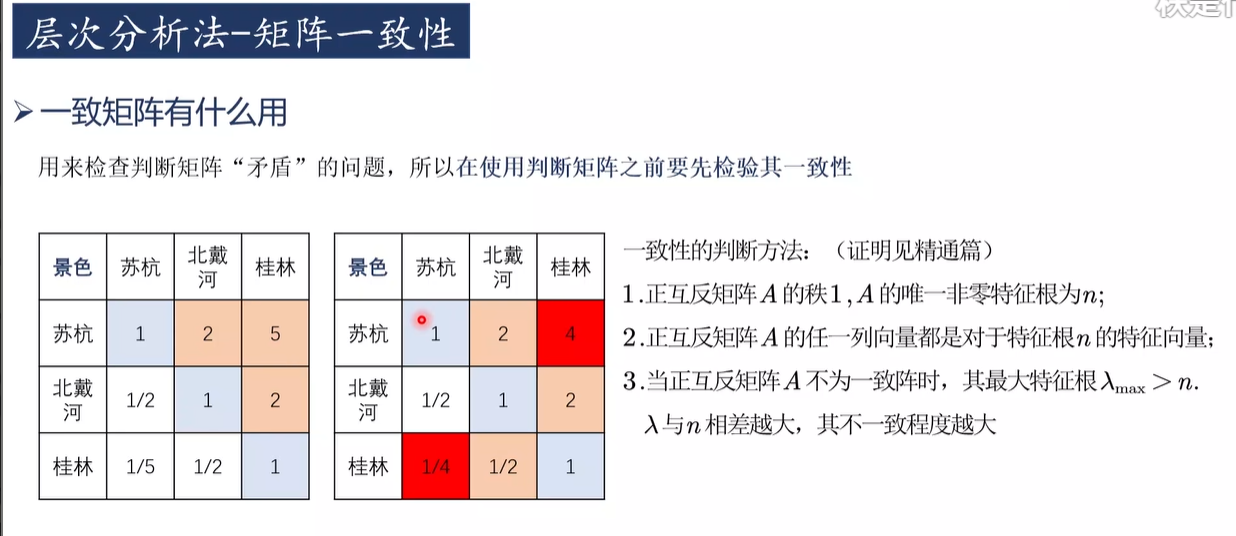
矩阵一致性

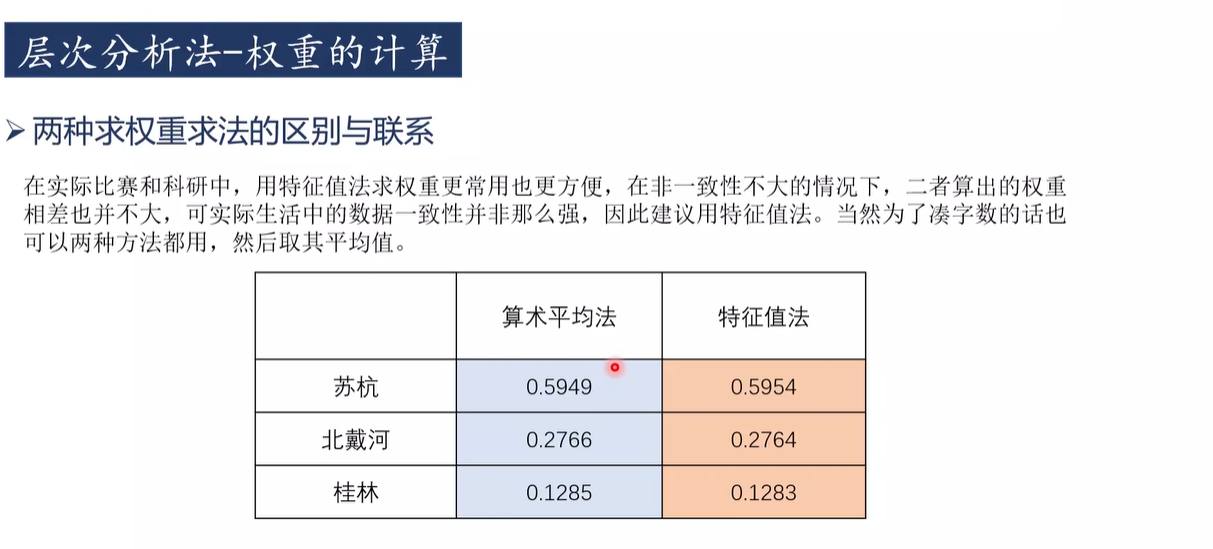
权重的计算

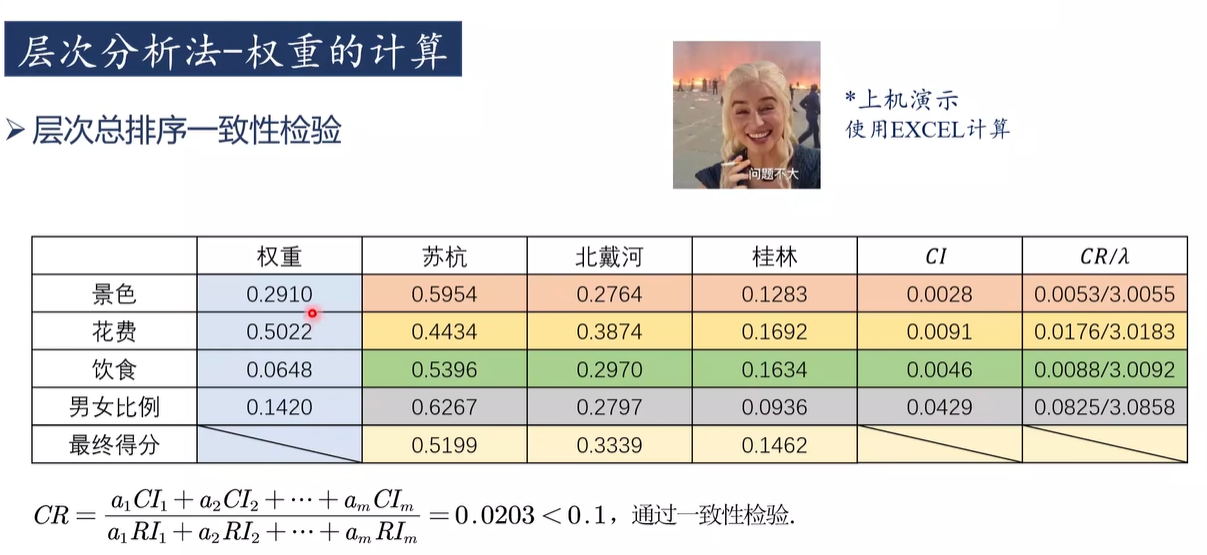
总结

应用

代码部分：

%% 层次分析法
% 只有非一致性才需要一致性检验

%% 获取判断矩阵
disp("请输入判断矩阵A:")
A = input('A=');
[n,n]=size(A);

%% 方法一：算数平均值求权重
sum_A = sum(A);
SUM_A = repmat(sum_A,n,1);
Stand_A = A./SUM_A;

disp("算数平均法求权重的结果为：")
w1 = sum(Stand_A,2)./n;
disp(w1);


%% 方法二：特征值法求权重
[V,D] = eig(A);
Max_eig =  max(max(D));
[r,c] = find(D == Max_eig, 1);
disp("特征值法求权重的结果为：");
w2 = V(:,c) ./ sum(V(:,c));
disp(w2);
disp("两种方法的平均权值为：");
disp((w1+w2)./2);



%% 计算一致性比例CR

CI = (Max_eig-n)/(n-1);
RI = [0.000,0.001,0.524,0.882,1.115,1.249,1.342,1.404,1.453,1.486,1.516,1.541,1.560,1.577,1.593];
% 这里的RI最多支持n=15,注意检查

% 这里的n=2时，RI=0,我们为了避免分母为0，将第二个元素修改为接近0的正数

CR = CI/RI(n);

disp(Max_eig);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR < 0.10
    disp("CR<0.10,该判断矩阵A的一致性可以接受");
else
    disp("注意：CR>=0.10，该判断矩阵需要进行修改！")
end

输出结果：

>> ccfx
请输入判断矩阵A:
A=[1,2,5;0.5,1,2;0.2,0.5,1]
算数平均法求权重的结果为：
    0.5949
    0.2766
    0.1285

特征值法求权重的结果为：
    0.5954
    0.2764
    0.1283

两种方法的平均权值为：
    0.5951
    0.2765
    0.1284

    3.0055

一致性指标CI=
    0.0028

一致性比例CR=
    0.0053

CR<0.10,该判断矩阵A的一致性可以接受
>>