P2698 [USACO12MAR] Flowerpot S （单调队列、离散化）

洛谷原题链接：https://www.luogu.com.cn/problem/P2698

P2698 [USACO12MAR] Flowerpot S

题目描述

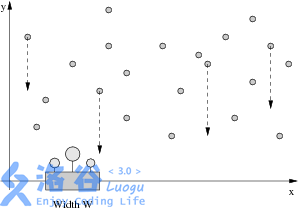
老板需要你帮忙浇花。给出 \(N\) 滴水的坐标，\(y\) 表示水滴的高度，\(x\) 表示它下落到 \(x\) 轴的位置。

每滴水以每秒 \(1\) 个单位长度的速度下落。你需要把花盆放在 \(x\) 轴上的某个位置，使得从被花盆接着的第 \(1\) 滴水开始，到被花盆接着的最后 \(1\) 滴水结束，之间的时间差至少为 \(D\)。

我们认为，只要水滴落到 \(x\) 轴上，与花盆的边沿对齐，就认为被接住。给出 \(N\) 滴水的坐标和 \(D\) 的大小，请算出最小的花盆的宽度 \(W\)。

输入格式

第一行 \(2\) 个整数 \(N\) 和 \(D\)。

接下来 \(N\) 行每行 \(2\) 个整数，表示水滴的坐标 \((x,y)\)。

输出格式

仅一行 \(1\) 个整数，表示最小的花盆的宽度。如果无法构造出足够宽的花盆，使得在 \(D\) 单位的时间接住满足要求的水滴，则输出 \(-1\)。

输入输出样例 #1

输入 #1

4 5
6 3
2 4
4 10
12 15

输出 #1

2

说明/提示

【样例解释】

有 \(4\) 滴水，\((6,3)\)，\((2,4)\)，\((4,10)\)，\((12,15)\)。水滴必须用至少 \(5\) 秒时间落入花盆。花盆的宽度为 \(2\) 是必须且足够的。把花盆放在 \(x=4\dots6\) 的位置，它可以接到 \(1\) 和 \(3\) 水滴，之间的时间差为 \(10-3=7\) 满足条件。

【数据范围】

\(40\%\) 的数据：\(1 \le N \le 1000\) ，\(1 \le D \le 2000\)。

\(100\%\) 的数据：\(1 \le N \le 10 ^ 5\)，\(1 \le D \le 10 ^ 6\)，\(0\le x,y\le10^6\)。

思路：

创建两个单调队列，一个维护窗口中最大值，一个维护窗口中最小值，由于水滴的x坐标不是连续的，所以进行离散化处理，然后将水滴的x坐标从小到大排序，每次循环左边界移动一位，有边界找到符合条件的最小右边界，按照单调队列的流程，更新区间的最大值和最小值，如果符合条件跳出循环，下面再进行判断一次，避免出现r已经处于n-1位置的情况下，无法继续移动，使得条件成立，错误更新答案的情况，每次更新取min，每次循环结束更新一次左边界

题解：

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
int n,d;
struct water
{
    int x,y;
}wa[N];

bool cmp(water a,water b)
{
    return a.x<=b.x;
}

int mindq[N];
int maxdq[N];

int mint,minh,maxh,maxt;

bool ok()
{
    int maxnum = maxt>maxh?wa[maxdq[maxh]].y:0;
    int minnum = mint>minh?wa[mindq[minh]].y:0;
    return maxnum-minnum>=d;
}

void push(int r)
{   
    while(maxh<maxt&&wa[maxdq[maxt-1]].y<=wa[r].y)
    {
        maxt--;
    }
    maxdq[maxt++]=r;
    while(minh<mint&&wa[mindq[mint-1]].y>=wa[r].y)
    {
        mint--;
    }
    mindq[mint++]=r;
}


void pop(int l)
{
    if(maxh<maxt&&maxdq[maxh]==l)maxh++;
    if(minh<mint&&mindq[minh]==l)minh++;
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>n>>d;
    for(int i=0;i<n;i++)cin>>wa[i].x>>wa[i].y;
    sort(wa,wa+n,cmp);
    // for(int i=0;i<n;i++)cout<<wa[i].x<<' '<<wa[i].y<<endl;
    int ans = INT_MAX;
    for(int l=0,r=0;l<n;l++)
    {
        while(!ok()&&r<n)
        {
            push(r++);
        }
        if(ok())ans = min(ans,wa[r-1].x-wa[l].x);
        pop(l);
    }
    if(ans==INT_MAX)cout<<-1<<endl;
    else cout<<ans<<endl;

    return 0;
}