CF453A Little Pony and Expected Maximum （动态规划，期望）

codeforces链接原题：https://codeforces.com/problemset/problem/453/A

CF453A Little Pony and Expected Maximum

题目描述

暮暮刚刚在和她的朋友——AJ（苹果杰克）、FS（小蝶）、RD（云宝黛西）玩Ludo游戏。但是她马品没攒够总是输。回到城堡过后，她对游戏用的骰子产生了兴趣。

这个骰子有M面：骰子的第一面有一个点，第二面有两个点，以此类推，第m面含有M点。暮暮确信的是，当掷骰子时，每一面都有1/m的可能性出现，并且每次投掷的概率都是都是独立的。请你帮助她计算掷N次骰子后每次得到的点数中最大值的期望。

输入格式

一行两个整数 m 和 n (1 ≤ m, n ≤ 10^5).

输出格式

输出一行一个实数，与答案误差不大于10^-4

输入输出样例 #1

输入 #1

6 1

输出 #1

3.500000000000

输入输出样例 #2

输入 #2

6 3

输出 #2

4.958333333333

输入输出样例 #3

输入 #3

2 2

输出 #3

1.750000000000

思路：

这道题目是一个期望dp的题目，第一次见，学习了
这道题目的意思是投掷n次后，投掷的这n次里，投出的数的最大值的期望
不难意识到，投掷次数越多，期望一定是越来越大的
接下来就是遍历投出最大值为i的情况，然后累加，就是最后的答案了
公式的话如下

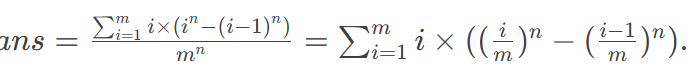
注意控制精度

题解：

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long ll;
double  m,n,ans;

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>m>>n;
    for(double i=1;i<=m;i++)
    {
        ans += i*(pow(i/m,n)-pow((i-1)/m,n));
    }
    printf("%.12lf\n",ans);
    return 0;
}