CF466C Number of Ways （前缀和）

codeforces原题链接：https://codeforces.com/problemset/problem/466/C

CF466C Number of Ways

题目描述

You've got array $ a[1],a[2],...,a[n] $ , consisting of $ n $ integers. Count the number of ways to split all the elements of the array into three contiguous parts so that the sum of elements in each part is the same.

More formally, you need to find the number of such pairs of indices $ i,j $ $ (2<=i<=j<=n-1) $ , that .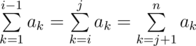

输入格式

The first line contains integer $ n $ $ (1<=n<=5·10^{5}) $ , showing how many numbers are in the array. The second line contains $ n $ integers $ a[1] $ , $ a[2] $ , ..., $ a[n] $ $ (|a[i]|<=10^{9}) $ — the elements of array $ a $ .

输出格式

Print a single integer — the number of ways to split the array into three parts with the same sum.

输入输出样例 #1

输入 #1

5
1 2 3 0 3

输出 #1

2

输入输出样例 #2

输入 #2

4
0 1 -1 0

输出 #2

1

输入输出样例 #3

输入 #3

2
4 1

输出 #3

0

思路：

这道题不难发现，可以利用前缀和更快捷的划分区间求和，将数组划分为3份，说明需要找到两个断点，在第一个断点前面的数字的和为所有数字加起来的sum的三分之一，而从索引1到第二个断点之间的数字之和则是sum的三分之二，而当sum无法被3整除时候一定无解，所以在前面可以对sum先进行一个特判，同时要对两个断点设定好满足条件，上题解

题解

#include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
typedef long long ll;
int n;
int a[N];
ll presum[N];
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    ll sum=0;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        sum+=a[i];
        presum[i]+=presum[i-1]+a[i];

    }
    if(sum%3)cout<<0<<endl;
    else
    {
        ll ans=0;
        ll cnt=0;
        ll div= sum/3 ;
        for(int i=1;i<n;i++)
        {
            if(presum[i]==(2*div)&&i<=n-1&&i>1)ans+=cnt;
            if(presum[i]==div&&i<=n-2)cnt++;
        }
        cout<<ans<<endl;
    }


    return 0;
}