一个二元函数的图像
import numpy as np
import matplotlib.pyplot as plt
# 生成数据
x0 = np.linspace(-3, 3, 100)
x1 = np.linspace(-3, 3, 100)
X0, X1 = np.meshgrid(x0, x1)
Z = X0**2 + X1**2
# 创建3D画布
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
# 绘制曲面
surf = ax.plot_surface(X0, X1, Z,
cmap='viridis', # 颜色映射
edgecolor='k', # 网格线颜色
alpha=0.8) # 透明度
#
# 坐标轴设置
ax.set_xlabel('$x_0$', fontsize=12)
ax.set_ylabel('$x_1$', fontsize=12)
ax.set_zlabel('$f(x)$', fontsize=12)
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
ax.set_zlim(0, 18)
# 添加颜色条
# fig.colorbar(surf, shrink=0.5, aspect=5)
# 视角调整(可选)
# ax.view_init(elev=30, azim=45) # 仰角30度,方位角45度
plt.show()
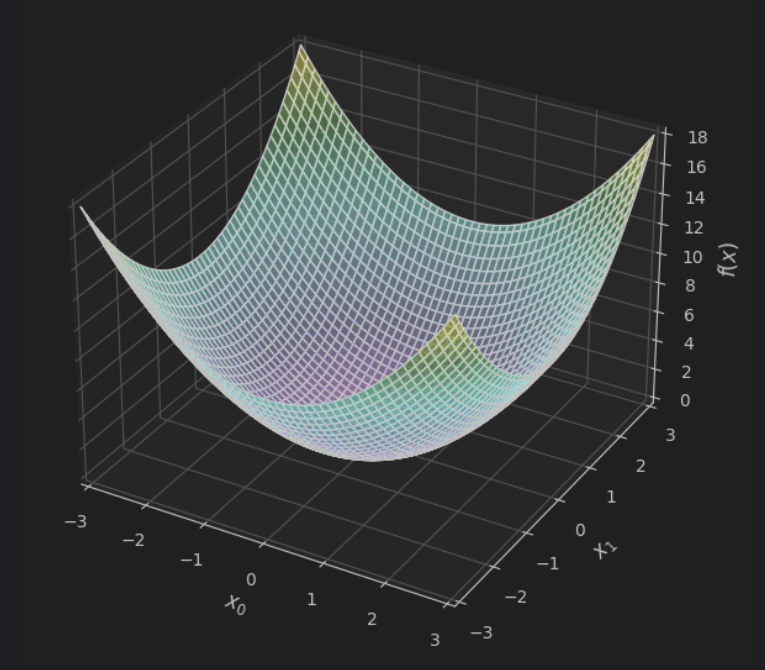
该函数的梯度图像
import numpy as np
import matplotlib.pyplot as plt
# 生成网格数据
x0 = np.linspace(-3, 3, 20) # 减少点数避免箭头过密
x1 = np.linspace(-3, 3, 20)
X0, X1 = np.meshgrid(x0, x1)
# 计算梯度(手动求导)
df_dx0 = 2 * X0 # 对x0的偏导数
df_dx1 = 2 * X1 # 对x1的偏导数
# 计算梯度幅值(箭头颜色)
grad_magnitude = np.sqrt(df_dx0**2 + df_dx1**2)
# 创建画布
plt.figure(figsize=(8, 6))
# 绘制梯度向量场
quiver = plt.quiver(X0, X1, df_dx0, df_dx1, grad_magnitude,
cmap='viridis', # 颜色映射
angles='xy', # 箭头方向基于xy坐标系
scale_units='xy', # 缩放单位一致
scale=30, # 箭头缩放比例(值越小箭头越大)
width=0.004, # 箭头宽度
headwidth=3) # 箭头头部宽度
# 添加颜色条
plt.colorbar(quiver, label='Gradient Magnitude')
# 图形装饰
plt.title('Gradient Vector Field of $f(x_0, x_1) = x_0^2 + x_1^2$', fontsize=12)
plt.xlabel('$x_0$', fontsize=12)
plt.ylabel('$x_1$', fontsize=12)
plt.grid(alpha=0.3)
plt.axis('equal') # 保持坐标轴比例一致
plt.show()
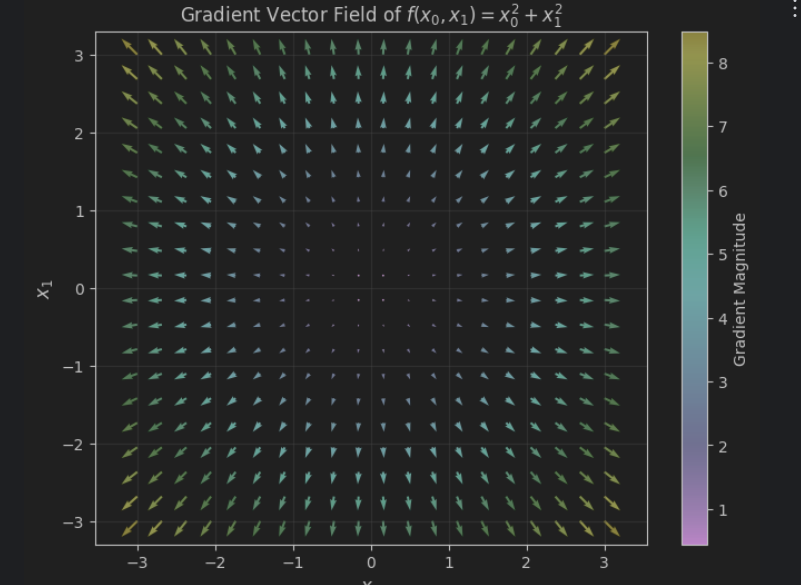
三维的梯度图像
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 生成数据
x0 = np.linspace(-3, 3, 10) # 稀疏网格避免箭头拥挤
x1 = np.linspace(-3, 3, 10)
X0, X1 = np.meshgrid(x0, x1)
Z = X0**2 + X1**2
# 计算梯度
df_dx0 = 2 * X0
df_dx1 = 2 * X1
df_dz = np.ones_like(Z) # 梯度在z方向的分量(投影到三维空间)
# 创建3D画布
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
# 绘制抛物面
ax.plot_surface(X0, X1, Z,
cmap='viridis',
alpha=0.7,
edgecolor='k')
# 绘制三维梯度箭头
ax.quiver(X0, X1, Z, # 箭头起点
df_dx0, df_dx1, df_dz, # 箭头分量
length=0.5, # 箭头长度
color='red', # 箭头颜色
normalize=True, # 归一化箭头长度(统一显示方向)
arrow_length_ratio=0.03) # 箭头头部比例
# 坐标轴设置
ax.set_xlabel('$x_0$', fontsize=12)
ax.set_ylabel('$x_1$', fontsize=12)
ax.set_zlabel('$f(x)$', fontsize=12)
ax.set_title('3D Gradient Visualization', fontsize=14)
plt.show()
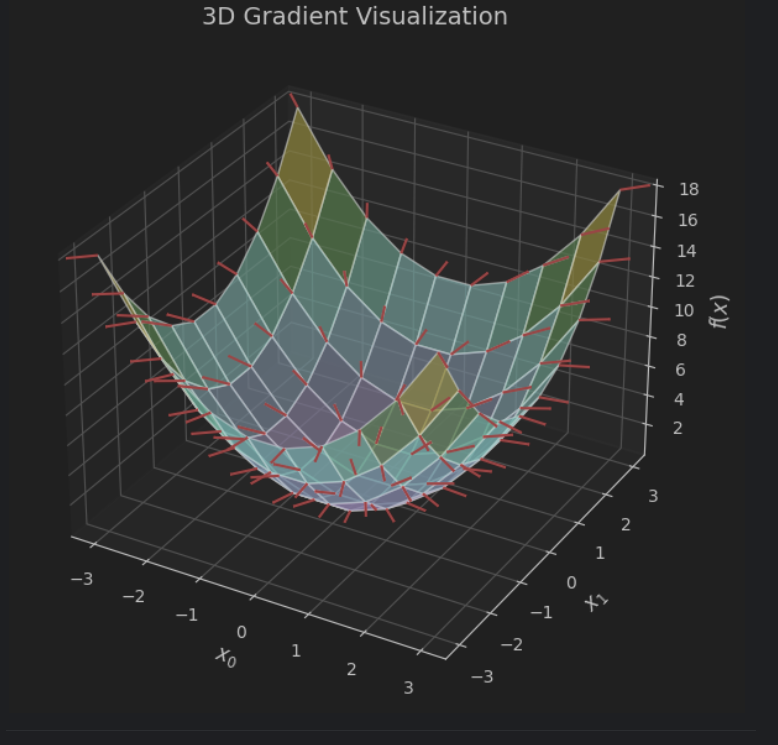
梯度下降法的实现
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx]=tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val -h
fxh2 = f(x)
grad[idx]=(fxh1 - fxh2) / (2*h)
x[idx] = tmp_val
return grad
def gradient_descend(f,init_x,lr =0.01,step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f,x)
x -= lr * grad
return x
def f(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0,4.0])
gradient_descend(f,init_x,lr=0.1,step_num=100)
梯度更新过程
import numpy as np
import matplotlib.pyplot as plt
# 定义目标函数和梯度
def f(x0, x1):
return x0**2 + x1**2
def gradient(x0, x1):
return np.array([2*x0, 2*x1]) # 梯度向量
# 梯度下降参数
initial_point = np.array([-3.0, 4.0]) # 初始位置
learning_rate = 0.1 # 学习率
max_iterations = 20 # 最大迭代次数
tolerance = 1e-6 # 收敛阈值
# 生成等高线数据
x0 = np.linspace(-4, 4, 100)
x1 = np.linspace(-5, 5, 100)
X0, X1 = np.meshgrid(x0, x1)
Z = f(X0, X1)
# 运行梯度下降
path = [initial_point.copy()]
current_point = initial_point.copy()
for _ in range(max_iterations):
grad = gradient(*current_point)
if np.linalg.norm(grad) < tolerance:
break
current_point -= learning_rate * grad
path.append(current_point.copy())
path = np.array(path)
# 可视化设置
plt.figure(figsize=(10, 6))
# 绘制等高线
contour = plt.contour(X0, X1, Z,
levels=np.logspace(0, 2, 10), # 指数间隔的等高线
cmap='gray',
linestyles='--',
linewidths=0.5)
plt.clabel(contour, inline=True, fontsize=8) # 添加等高线数值标签
# 绘制梯度下降路径
plt.plot(path[:,0], path[:,1],
'o-', # 圆形标记+实线
color='#FF6347', # 番茄红色
markersize=8,
linewidth=2,
markeredgecolor='black',
label='Gradient Descent Path')
# 添加路径箭头
for i in range(1, len(path)):
dx = path[i,0] - path[i-1,0]
dy = path[i,1] - path[i-1,1]
plt.arrow(path[i-1,0], path[i-1,1], dx*0.8, dy*0.8, # 缩短箭头避免重叠
shape='full',
color='dodgerblue',
width=0.02,
head_width=0.3)
# 标注特殊点
plt.scatter(*initial_point, s=150, zorder=3,
marker='*',
color='gold',
edgecolor='black',
label='Start (-3, 4)')
plt.scatter(0, 0, s=100,
marker='X',
color='limegreen',
edgecolor='black',
label='Minimum (0, 0)')
# 图形装饰
plt.title("Gradient Descent on $f(x_0, x_1) = x_0^2 + x_1^2$", fontsize=14)
plt.xlabel('$x_0$', fontsize=12)
plt.ylabel('$x_1$', fontsize=12)
plt.xlim(-3.5, 1)
plt.ylim(-1, 4.5)
plt.grid(alpha=0.3)
plt.legend(loc='upper right')
plt.gca().set_aspect('equal') # 保持坐标轴比例一致
plt.show()
SGD 随机梯度下降法
from torch import sigmoid, softmax
import sys, os
sys.path.append(os.pardir)
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size,
weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:输入数据, t:监督数据
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = (numerical_gradient(loss_W, self.params['W1']))
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads





 浙公网安备 33010602011771号
浙公网安备 33010602011771号