20年Selection rules for quasibound states in the continuum-用群论研究了所有能带折叠的情况-这篇好像与Rashba效应有关，与手性有关！ 引用也很高，200. 我完全没懂这篇，需要花大量时间仔细研究文献[66]这本书以及群论

20年Selection rules for quasibound states in the continuum-用群论研究了所有能带折叠的情况-这篇好像与Rashba效应有关，必须读！ 与手性有关！ 引用也很高，200. 我完全没懂这篇，需要花大量时间仔细研究文献[66]这本书以及群论

目录

Phys. Rev. B 102, 035434 (2020) - Selection rules for quasibound states in the continuum (aps.org)

Overvig-2020-Selection rules for quasibound st.pdf

‍

六种类型的二维PCS晶格中的面内对称性破缺控制的对称保护BIC的选择规则（如果以及发生自由空间偏振耦合）的详尽目录。

光子晶体板 （PCS） 是一类经过充分研究的器件，已知它支持通常入射到板的光的光学 Fano 共振(见02年导模共振论文，注意02年导模共振论文中说，可以从透射谱的尖锐线形计算出Q因子)，可用于窄带滤波器、调制器和非线性光子器件。在浅蚀刻PCS中，通过调整蚀刻深度，可以很容易地控制共振的线宽。这种设计优势是以由于光能量的平面内局域较差而导致器件占用空间大为代价的。在高折射率对比度材料系统中实现的全蚀刻 PCS 中，平面内局域得到了极大的改善，但对线宽的控制受到了影响。全蚀刻 PCS（也称为高对比度光栅 （HCG）） 中的这一缺点可以通过访问对称保护BIC来克服。通过扰动 HCG，BIC 可以从自由空间激发，其品质因子显示出与扰动大小成反平方的依赖性，同时继承了未扰动对应物的出色平面内局域（其实扰动之后就成为了QBIC，Q因子比BIC低一些，但还是挺高）。在这里，我们报告了由六种类型的二维PCS晶格中的面内对称性破缺控制的对称保护BIC的选择规则（如果以及发生自由空间偏振耦合）的详尽目录。所选晶格允许访问未受扰动的方形和六边形 PCS 的三个最高对称模式类。与面外对称性破坏相比，对面内对称性破坏的限制允许使用简单的光刻制造技术制造设备，这在实际应用中很有用。报告的方法为设计PCS提供了一个高级路线图，该PCS支持可控的锐利光谱特征，使用成熟的制造平台以最小的器件尺寸。为了演示由此产生的结构"字母表"的使用，我们数值演示了用于太赫兹生成、机械可调光学寿命和仅在共振时进行波前整形的非局部超表面平台。

全蚀刻 光子晶体板PCS（也称为高对比度光栅 （HCG））

‍

光子晶体板的用处：可用于窄带滤波器、调制器和非线性光子器件。

‍

引言

增强光-物质相互作用是改进和扩展各种光子设备功能的关键能力。对光进行空间和时间限制可实现具有快速开关速度的紧凑型平面光调制器 [1-4]、窄带带通滤波器 [5-9]、灵敏的生物和折射率传感器 [10-12]、高效的光学微机电设备 [13,14]、新型激光器 [15-19]，以及增强非线性 [20-23] 和量子光学现象 [24,25]。传统的方法是引入光腔，使光能循环，让光子多次穿过材料。

平面衍射光学技术可在轻质准二维系统中实现独特的紧凑光学约束，该系统由成熟的微型和纳米制造技术制造而成。传统的等离子材料（如金）可在元表面产生强烈的光物质相互作用 [23,26-30]，但与标准的互补金属氧化物半导体（CMOS）代工厂不兼容。替代性质子材料是一个活跃的研究领域[31,32]，但无一例外都会带来巨大的光学损耗，从而降低光子设备的效率。这些限制促使人们探索在不使用金属的情况下限制光能的方法，将光学材料限制在硅及其氧化物等常见介电材料上。

低对比度光栅（LCG）或导模共振滤波器 [5-8]，就是增强光-物质相互作用的介质衍射光学元件的一个典型例子。通过周期性地波纹化亚波长周期性薄板，由薄板支持的横向传播波导模式可与正常入射光耦合。The leakage out of the slab interferes with the direct optical pathways（此处为法布里-珀罗共振），产生著名的法诺共振 [33-35]。

这句话可以从 02年Fan-2002-Analysis of guided resonances in photonic crystal slabs[1] 中，其实就是在说两个路径的干涉：因此，整个透射谱图7，就是取决于直接和间接路径的干涉。【其实就是说有两种路径】[2]

从伍德反常Wood's anomalie现象开始，人们对相关现象的研究已经持续了一个多世纪 [36-38]。在 LCG 中，波纹的程度可以很容易地通过实验进行控制，它是一个直接控制共振谱特征线宽的设计参数。特别是，对于小波纹，品质因数 ( Q 系数）与波纹深度成反比 [39]。然而，这一诱人的设计特点也有其固有的缺点： 长的光学寿命来自于导波模式在耦合回自由空间之前在器件内的长距离传播；因此，器件的横向尺寸必须与这一特征传播距离相当，才能观测到窄光谱特征。换句话说，LCG 受限于空间限制（器件尺寸）和时间限制（Q 值）之间的权衡。

全蚀刻 PCS（也称为高对比度光栅 （HCG））不容易像LCG一样容易控制Q值。
全蚀刻 PCS的优点：高对比度光栅能够通过大的面内布拉格反射横向限制光能，从而实现紧凑型器件

另一种经过深入研究的衍射光学元件是高对比度光栅（HCG） [40-42]，众所周知，高对比度光栅能够通过大的面内布拉格反射横向限制光能，从而实现紧凑型器件。由于 HCG 的波纹很深（而且通常很完整） ，因此在LCG中提出的容易控制Q值的方法对于HCG来说是缺失的。因此，HCG 以其宽带光谱特性而著称。 不过，众所周知，HCG 也支持法诺共振形式的尖锐光谱特征 [42-44]（指的是透射谱、反射谱，见02年导模共振论文）。特别是对于某些光学材料、几何形状、波长、角度和偏振的组合，HCG 中的 Q 因子可能变得无限大，这种现象被称为 "连续体中的束缚态" （BIC） [45-48]。在相关多维参数空间中的 BIC 附近操作，可以调整共振的有限 Q 因子。遗憾的是，由于同时对许多参数具有复杂而敏感的依赖性，这种控制与 LCG 中的控制相比并不稳健robust。

HCG 中受对称性保护的 BIC 比意外的 BIC 更适合制造具有尖锐光谱特征的紧凑型光学器件。

不过，HCG 可以支持两类 BIC：一类是由于对称性限制而被排除在与自由空间耦合之外的 BIC（或称 "对称性保护 "BIC），另一类是由于与对称性无关的原因而被排除在外的 BIC（或称 "意外 "BIC [49]）。最近有观点认为 [50]，HCG 中受对称性保护的 BIC 比意外的 BIC 更适合制造具有尖锐光谱特征的紧凑型光学器件。众所周知，通过降低 HCG 或 PCS 的对称性 [9,28,51-60]，受对称性保护的 BIC 在连续体中会变得准束缚，此时它们被称为 "准 BIC" [61]。

准BIC是由对称保护BIC变换过来的！
准 BIC 在沿法线入射条件下与光耦合，其光学寿命受制于打破保护它们的对称性的扰动大小，thereby restoring a robust design paradigm for controlling the Q factor of a sharp spectral feature。

此外，最近的研究还表明 [54,60]，适当的扰动（包括打破垂直对称性）可以很好地控制能带结构。因此，对称性被打破的 HCG 继承了 LCG 和 HCG 在紧凑型器件中与尖锐光谱特征相关的优点。

即继承了"高对比度光栅能够通过大的面内布拉格反射横向限制光能，从而实现紧凑型器件。"这个优点 以及 LCG的Q因子可调这个优点

布里渊区折叠的效果：a period doubling perturbation (a dimerization of an HCG) allows modes previously bound [under the light line at the edge of the first Brillouin zone (FBZ)] to be brought into the continuum,，与接近法线入射角的一系列角度耦合，

特别是，a period doubling perturbation (a dimerization of an HCG) allows modes previously bound [under the light line at the edge of the first Brillouin zone (FBZ)] to be brought into the continuum,，与接近法线入射角的一系列角度耦合，在某种程度上，这种耦合完全由扰动控制[53-56,60,62,63]。

to a degree: 在某种程度上

因此，"二聚化高对比度光栅"（DHCG [50]）是实现光的空间和时间限制的平面光学器件的绝佳候选平台。

时间限制指的是 Q因子。 空间限制指的是 光局域在板中，即QBIC 会局域在板中，且不与外界耦合。

注意区分 准导模共振，QGM，就是23年那篇QGM的论文说的。

对 DHCG 的研究大多集中在简单的一维器件上，这种器件可以控制一个平面内方向的模式，但不能控制正交方向的模式。具有周期性扰动的二维高对比度 PCS 是 DHCG 的自然延伸，它解决了这一限制，也是本文的主题。与简单的一维情况相比，二维 PCS 的对称性数量要多得多；因此，需要对自由空间与具有周期性扰动的二维 PCS 之间丰富的模态相互作用进行详细探讨。

对称保护 BIC 通常在单原子 PCS 中进行研究，在这种情况下，偶数/奇数对称条件可能会排除在发现入射时与自由空间的耦合。

这句话说的就是对称保护BIC：对称性保护的连续体束缚态（Symmetry-protected BIC）[3]，Gamma点

双原子 PCS（如 DHCG）

双原子 PCS（如 DHCG） 中的 BIC 受制于类似的偶/奇对称条件，因此一旦周期倍增将束缚模式折叠到连续体中，它们仍可能被束缚在连续体中。【即仍然可能存在BIC】

如果相关的偶/奇对称性被打破，受对称性保护的 BIC 就会变成准 BIC。单原子和双原子方法属于同一类受对称保护的 BIC，但可以进入不同的高对称模式（即具有不同周期性和场剖面的模式） 。

因此，为了充分利用可用的扰动和模式，我们同时研究了单原子和多原子 PCS。

我们注意到，打破相关面内对称性的最简单方法是以刚好偏离基底法线的入射角激发准 BIC。 然而，正如文献[50]所指出的，这种方法受到限制。[50]，与通过扰动结构来打破对称性相比，这种方法具有局限性。特别是，这种方法只适用于以精确角度为中心的光动量角散布有限的光（为了得到目标的 Q 因子），因此需要大面积的设备，以及设备相对于光源光学器件的精确倾斜。

最后，虽然我们在本文中描述的是由全介质 PCS 支持的准 BIC，但我们注意到，只要材料是各向同性的，这里采用的群论方法对任何材料系统都是有效的。 例如，硅柱阵列与硅板（甚至金属板）上的孔阵列的处理方法相同。可以根据应用需要选择材料系统；尽管场剖面和共振频率千差万别，但仍会存在一组遵循本文推导的选择规则的类似模式（按其面内对称性分类）。

‍

本文：准 BIC 的选择规则目录-可以指导器件设计

在本文中，我们将研究应用于高对称性 PCS 晶格的面内扰动所引起的光学响应。在整个研究过程中，我们假定这些 PCS 在面外方向具有不变的横截面，并假定由于基底的存在而引入的面外对称性可以忽略不计。在第 II 章 A 节中，我们回顾了准 BIC 及其如何在空间和时间上限制光。在第二节 B 中，我们用群论的语言回顾了正方形和六边形 PCS 各自支持的三类高对称性模式（共六类模式）的分类。第三节 A 部分探讨了针对这六种高对称性模式而选择的六类扰动晶格。 为了确定这些扰动的影响，第 III B 节推导了对称约束耦合条件，规定了扰动时自由空间极化的耦合情况（如果有的话） 。在第 III C 节中，应用群论原理写出了每种模式和每个空间群的偏振依赖性。结果是一份准 BIC 的选择规则目录，描述了方形和六角形光子晶体晶格的六种最高对称模式可通过平面内对称破缺进入的所有独特方式。 最后，在第四节中，我们讨论了目录中值得注意的方面，并简要介绍了几个器件应用实例。特别是，在这里和随附论文[64]中，我们展示了目录如何指导器件设计，利用连续扰动实现光学光谱的多功能控制，并介绍了一类新型元表面，利用这种多功能控制来空间控制谐振波面。

‍

背景

A. 连续体中的准约束态

我们首先回顾了创建有限尺寸 DHCG 的设计过程；我们在图 1(a) 中艺术性地描绘了一个二元晶格中的 BIC。图 1(b) 和图 1(c) 分别定义了未扰动晶格和扰动晶格的几何参数。 扰动晶格中的两个 "原子"（此处为硅柱）高度相同 𝐻 和直径 𝐷 相同，并位于周期为 2 𝑃 其中 𝑃 是未扰动晶格的周期。扰动可量化为原子间的间隙： 扰动间隙为 \(𝑔_2\)= 𝑔 + 𝛿 ,其中 𝑔 是未扰动间隙 ( 𝑔 = 𝑃 - 𝐷 )和 𝛿 为扰动。图 1(d)和图 1(e)分别显示了未扰动晶格和扰动晶格的 FBZ，图中定义了高对称点。晶格变换的影响 （将实际空间中的周期从 𝑃 到 2 𝑃 并将基向量旋转 45 ° ) 是缩小 FBZ 的范围，并将其旋转 45 ° .

重要:折叠前和折叠后的态的关系:根据布洛赫定理，属于未扰动 FBZ 部分的态位于新的扰动 FBZ 之外，等同于新 FBZ 内的态。

如图 1(e)所示，它们通过倒易点阵矢量的平移被带入新的 FBZ 中（这一过程被称为布里渊区折叠）。 𝑋 点附近阴影区域的图形。在 𝑋 点的约束模态现在位于 Γ 点（即在连续体中）。

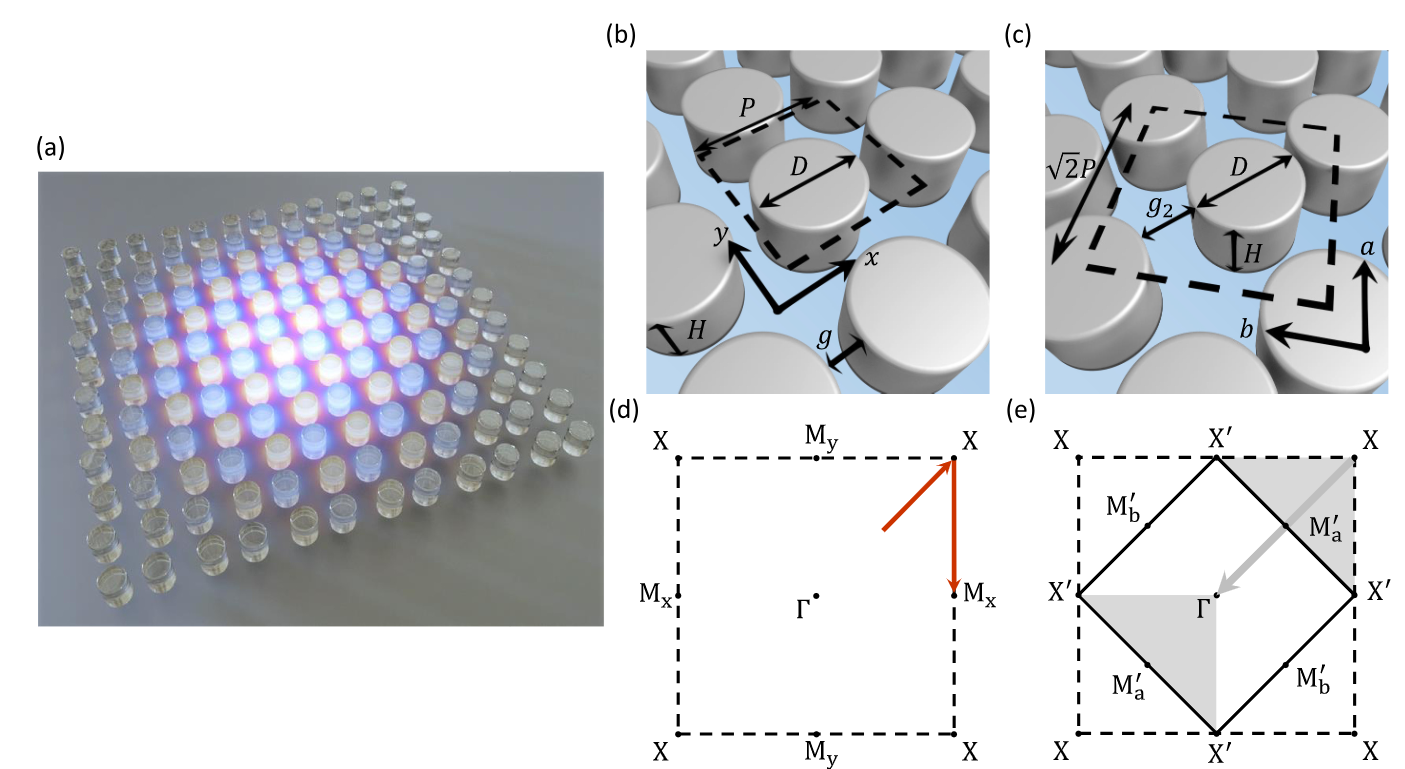
image

(a) 周期性扰动方晶格中连续体准结合态的艺术效果图。(b) 未扰动晶格的几何形状。(c) 扰动晶格的几何形状。(d) 未扰动晶格的第一布里渊区，红色箭头描绘了 (i) 带图中使用的路径。(e) 受扰动晶格的第一布里渊区，显示带状折叠。

折叠后能带图应该扫描的路径：注意(i)图是进行微扰后的结构的能带。其横坐标路径可以见图d和e，特别是d图中红色箭头就是 (i) 带图中使用的路径 ！

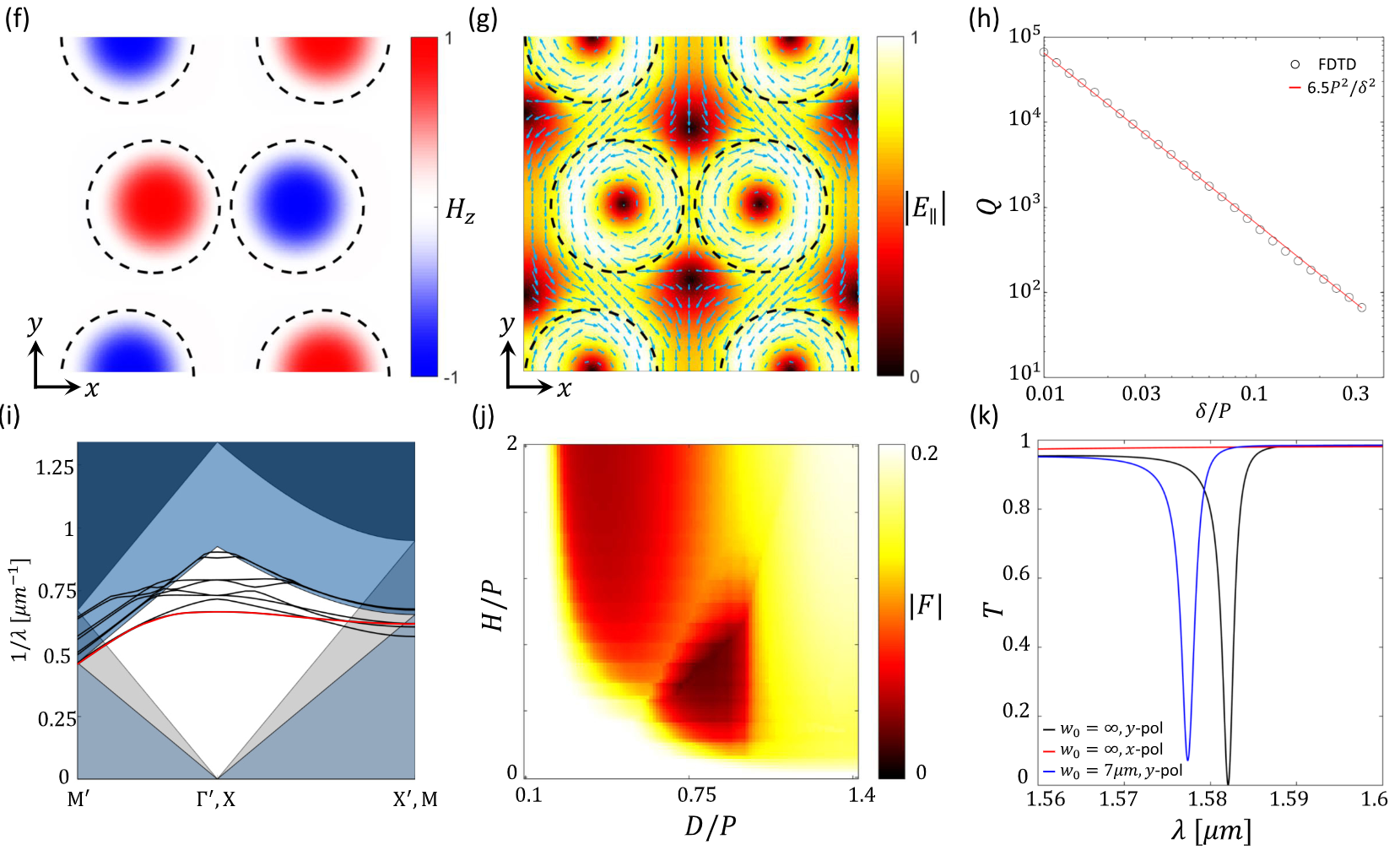image(f），（g）扰动晶格基本模式的面外磁场和面内电场分量。(h) 𝑄 系数与扰动的关系、 𝛿 = 𝑔_2 - 𝑔 . Overvig-2020-Selection rules for quasibound st.pdf - p4 - (i) Overvig-2020-Selection rules for quasibound st.pdf - p4 - Band diagram (with target band highlighted in red) Overvig-2020-Selection rules for quasibound st.pdf - p4 - of the folded modes in a finite height PCS with D = 0.411 μm, H = 0.295 μm, P = 0.527 μm. These parameters correspond to an operating wavelength of λ = 1.58 μm with the optimal (minimal) figure of merit |F | as found by the parameter sweep in (j), in which |F | is mapped for varying D/P and H/P. Overvig-2020-Selection rules for quasibound st.pdf - p4 - The taller diamondlike window in(i) represents the region of energy-momentum space where the superstrate (air) supports only a single diffractive order (m = 0);Overvig-2020-Selection rules for quasibound st.pdf - p4 - the shorter window represents the same for the substrate (silicon dioxide). (k) Transmittance T near the fundamental mode frequency of an infinitely periodic device excited by a plane wave at normal incidence and of a finite device (30 μm × 30 μm) with δ = 80 nm excited by a Gaussian beam with e−2 waist radius of w0 = 7 μm. Both devices show Q ≈ 1000 and excellent resonance visibility, indicating that the performance of the finite device is maintained despite its small footprint.

"Overvig-2020-Selection rules for quasibound st.pdf - p4 - The taller diamondlike window in(i) represents the region of energy-momentum space where the superstrate (air) supports only a single diffractive order (m = 0);"

什么是支持零级衍射的能量动量区域？注意，这并不是光锥，是一个比光锥更小的范围

零级衍射范围，在物理光学书172页中，圆孔的夫琅和费衍射，中间是一个圆，光能量大部分集中在中央亮斑，艾里斑。 （注意从图5.37可以看出，是在动量空间）[4]

有限结构和周期结构的Q因子都是1000，而且展现出优秀的共振可见性。这实际上就是Rashba那篇论文，通过能带折叠，实现了QGM！ 但实际上在远场图中，第一BZ和第二BZ的相差一个新倒格矢的同一能带的点，在远场图中还是会有区别。

Overvig-2020-Selection rules for quasibound st.pdf - p4 - Both devices show Q ≈ 1000 and excellent resonance visibility, indicating that the performance of the finite device is maintained despite its small footprint.

‍

通过BZ折叠引入连续域的新模式现在可以耦合到自由空间，并在法线入射光下产生类似法诺的尖锐光谱特征。

透射谱是fano线形，说明可以与自由空间耦合，是导模共振。 见02年导模共振论文。

根据构造，与自由空间之间的耦合强度 与扰动的大小有关。研究表明 [50]，扰动的耦合强度为 𝛿 量级. 由于 𝑄 因子与耦合强度的平方成反比 [39]，

因此受对称保护的 BIC 的 𝑄 因子受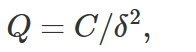image (1) [50,61] 约束。

其中常数 𝐶 会因模式、几何形状、材料和偏振而变化。图 1(f) 和 1(g) 显示了图 1(a) 所示基本模式的模式剖面。图 1(h) 显示了对 𝑄 因子随扰动强度变化的全波模拟结果。 . 图 1(i) 包含使用超级椭球方法的平面波展开法（PWEM）计算的扰动结构带图，其中定义了相对于未扰动晶格和扰动晶格的高对称点。按照图 1(d)中的红色箭头计算未扰动结构中的模式，然后将其人为折叠到 FBZ 中。

Γ 点附近的波段曲率对"由高斯光束激发的有限器件"可达到的 Q 因子有一个上限。

图 1(i)中扰动 PCS 的带状结构有助于预测对于有限器件，公式 (1) 的准确性。在无限器件中，平面波对应于单一状态（例如，在 Γ 点的模式），带曲率与之无关。然而，由高斯光束激发的有限器件将表现为由组成该高斯光束的平面波激发的响应的某种组合。预测有限器件行为的一个简单模型是对构成平面波的相应谱进行加权求和[50]。我们通过关于 Γ 点的泰勒展开来建立带模型、 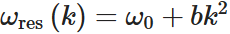image 其中 𝜔 0 是位于 𝑘 = 0 的模式的角频率 和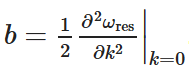image . A Gaussian beam with a characteristic spread in wave vector of Δk will excite a characteristic spread of frequencies 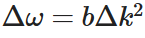image . 我们可以很自然地想到，如果这个频率分布大于共振线宽 𝑑 𝜔 ，光谱特征就会被冲掉，从而降低观测到的 𝑄 并使公式 (1) 失效。这就提出了一个约束条件

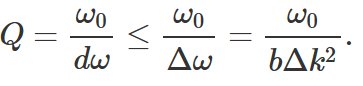image（2）

换句话说，Γ 点附近的波段曲率对有限器件可达到的 Q 因子有一个上限。

注意上式还表现了Q因子的定义,在02年导模共振论文中也有

虽然这个简单的模型并没有考虑到所有可能的有限尺寸效应（如边缘效应和更复杂的模态结构），但推导出的约束条件表明，优化频带平坦度往往能实现最紧凑的器件。 特别是，需要最小化的因子是 F = | b | / ω 0 （从(2)知，确实），F这个值可以作为在设计器件时，可通过计算其带状结构来确定其优劣。

image

‍

怎么优化几何参数，从而让计算波长优化到实验所需的共振波长：

Overvig-2020-Selection rules for quasibound st.pdf - p3 - We choose a design with the smallest F according to Fig. 1(j) and scale its geometrical parameters by a factorλ/λres such that the operating resonant wavelength is λ =1.58 μm for a calculated resonant wavelength λres .

such that ：以致于

‍

对于由高斯光束激发的有限结构,具有高Q，\(10^3\)

我们选择最小的设计 F 我们根据图 1(j)选择了一个 F 最小的设计，并将其几何参数按系数 λ / λ res 使工作谐振波长为 λ = 1.58 μ m 计算出的谐振波长 λ 谐振 . 图 1(k)显示了通过全波模拟计算出的无限周期器件的透射率光谱，该器件由一平面波激发，波长为 x 或 y 极化激发的平面波计算出的透射光谱，表明这种耦合只发生在 y 偏振。图 1(k)还显示了有限尺寸器件（30 毫米）的透射光谱。 30 μ m × 30 μ m ）激发的高斯光束的腰半径为 w 0 = 7 μ m 通过全波模拟计算得出。频谱特征保持不变，这证实了通过图 1(j) 所示的优化确定的图 1(i) 中的平坦频带可实现具有适度高 Q 值的紧凑型器件。 Q ≈ 10 3 .

特别注意，上面这部分讲解了优化器件设计的过程：3个步骤

图 1 概述了一个紧凑型光学器件（二维 DHCG）的设计过程，该器件因准 BIC 而支持尖锐的光谱特征（尖锐光谱特征说明会与外界进行耦合）。然而，这一过程只代表了一种高对称模式，并且只探索了一种特定扰动所导致的行为。结果表明，这种行为与入射角关系不大[图 1(i)] ，但与入射偏振关系很大[图 1(k)]。

对”所有高对称模式和扰动“ 的"​偏振行为（选择规则） " ​进行了理论描述，这一成果（我们称之为 "选择规则目录"）

本文的主要成果是对”所有高对称模式和扰动“ 的"偏振行为（选择规则）" 进行了理论描述。有了这一成果（我们称之为 "选择规则目录"），

图 1 中概述的设计过程可概括为三个步骤： (1) 根据高对称模式的实空间特性（如在高折射率材料中的场重叠）​选择一个高对称模式；(2) 通过调整未扰动结构中的参数来​优化能带结构 [如图 1(i)] ；(3) 根据所需的选择规则选择一个适当的扰动（如将目标指向 y 极化）。目录为步骤（3）提供了全面指导，结合步骤（1）对所需高对称性模式的选择，明确了丰富的选项；从而为这三步设计过程提供了一个高层次的路线图，最终设计出在空间和时间上都能限制光的 PCS。这种设计方案可进一步与计算反向设计技术[65]相结合，以缩小待探索的设计参数空间的尺寸。

‍

B. 高对称性模式的分类

确定扰动 PCS 选择规则的第一步是对存在的模式进行分类。由于选择规则源于对称性破缺，因此采用允许模式的对称性进行模式分类是自然而然的选择。虽然最终的器件是三维性质的（在平面外方向具有有限的厚度），但它的对称性是非常重要的，但从二维的麦克斯韦方程入手可以大大简化分析。在这种情况下，麦克斯韦旋度方程解耦为两个独立的三方程组，每个方程组都定义了以平面外磁场为特征的模式 𝐻 𝑧 (称为 TE 模式）或平面外电场 𝐸 𝑧 (称为 TM 模式）。然后，每个模式都可以通过这个单一的场分量来定义。因此，我们选择、回顾并执行了参考文献 [66]中详述的群论方法，对模式进行分类。[66] 中详述的群论方法，根据平面外场分量的平面内对称性对模式进行分类。我们注意到，这种群论分析适用于任何材料系统，例如硅柱阵列、硅片上的孔洞，甚至金属结构。为方便起见，并与传统的元表面进行比较，我们首先考虑硅柱阵列。但由此得出的选择规则可立即应用于任何其他材料系统。

  • 文献66就是光子晶体中的光学性质那本书
根据平面外场分量的平面内对称性对模式进行分类

由于场存在于周期性晶格中，它们的特征是平面波，其大小和方向与倒易晶格的高对称点相对应。当折射率对比度较低时，这种特性非常出色；当折射率对比度较大时（如硅和空气系统） ，相对于低折射率对比度系统，共振频率会出现显著偏差，但可能的模式的对称性保持不变。因此，​可以参照扩展区方案来研究这些模式。

图 2(a) 描述了正方形晶格的扩展区方案，并标出了显著的高对称点。image . 这些点具有点群对称性 𝐶 4 𝑣 , 𝐶 2 𝑣 和 𝐶 4 𝑣 和 𝐶 4 𝑣（有关特性表和其他相关群论表见附录 A），Overvig-2020-Selection rules for quasibound st.pdf - p5 - , and the modes decomposable by plane waves corresponding to these points are describable by these point groups.。这三组点是倒易网格中的最高对称点，因此对应于方格网格中的相关模态。六方格[图 2(b)]中的三组类似点是 Γ 点、 𝑀 点，以及 𝐾 点。

群论方法[66-68]预测了扩展区方案中每组高对称点的模式数量和性质。图 2(c) 中的表格总结了方形晶格中每个高对称点可能出现的模式。一组高对称点 N 的简并程度也就是该组高对称点对应的模式数。一组平面波的波向量 k 的大小将对应于模式的预期特征频率（然而，如上所述，在高指数对比度系统中，这种对应关系并不理想）。最后，不可还原表示法描述了模式对称性。也就是说，扩展区中列出的每个不可还原表征的 "相似变换"（共享其所有对称性）模式将出现在该扩展区中。需要注意的是，E 不可还原表示是双重简并的，因此包含两种模式。

图 3 和图 4 分别描述了正方形和六边形晶格中每个高对称点的前四个扩展区的 TM 模式。TE 模式也有类似的集合，对称性相同（以 H z 代替 E z），但空间扭曲，特征频率不同。这些模式按扩展区阶（列）和不可还原表示（行）排列。参考相关字符表[附录 A，图 17(a)]可知，以特定不可还原表示法标注的模式与字符表中相应行的转换方式相同：该行某列中的 1 表示该模态在该列的运算类下是对称的；- 1 表示反对称；0 表示不对称；大小为 2 表示该模态是简并的。

最后，模态的平面外特性是由 Z 方向上 PCS 每个原子的阶数 n 或反节点数来表征的。如果 PCS 具有关于 x y 平面的镜像对称性，则面外特性包含了本文讨论范围内的所有相关模态特征。

然而，众所周知，带有衬底的二维 PCS 会表现出手性行为：入射的圆偏振光的行为方式取决于手性[62,69]。基底和垂直对称破缺的手性效应超出了本文的研究范围，是未来研究的一个富有成果的方向。我们仅限于研究由垂直挤压的二维晶格组成的 PCS，我们发现低折射率基底（如玻璃）的存在通常不会产生什么实际影响（因此可以忽略）。

‍

法线入射时，研究二维PC 与有限厚度PCS,是一样的。因为：

重要的是，我们讨论了二维模式描述与有限厚度 PCS 模式之间的关系，本文始终假定有限厚度 PCS 在 Z 方向上是简单挤压的（其横截面是不变的）。图 3 和图 4 所示的模式可视为半无限二维光子晶体中沿 Z 方向移动的模式。在这种情况下，这些特征模是通过折叠无图案各向同性介质（即平面波，即就是一个纯板子，没有刻孔）的特征模来描述的。而在有限 PCS 中，正如文献[66]所讨论的，特征模是通过折叠无图案板的特征模来描述的。[66]，特征模态是通过折叠无图案板的特征模态来描述的。虽然基础不同，但所产生的模态对称性是相同的。然而，由于厚度有限，在 PCS 中会出现polarization混合现象（指的是TE和TM混合），从而产生准 TE 和准 TM 模态，而不是纯模态。 但是，由于垂直挤压和法线入射光线，新的偏振分量不会引入或破坏任何对称性，对称性由点群描述；也就是说，准 TE（准 TM）模式的 TM（TE）成分与类似的纯 TE（纯 TM）模式具有等效的对称性， and therefore have no bearing on the selection rules for normally incident light.。因此，我们将准 TE（准 TM）模式简称为 TE（TM），并将 PCS 模式等同于其二维对应模式，以便研究法线入射时的选择规则。

‍

与二维模式相比，PCS 模式还可能具有额外的平面外对称性。

如果存在 x y 镜像平面（位于 PCS 的中心），那么此处使用的点群就不足以描述模态。例如，六边形晶格的模式可以用二面体群来描述 D 6 h = C 6 v ⊗ C 1 h 其中 C 1 h 组表示模式相对于该模式是对称还是不对称的 x y 镜像平面对称还是不对称。这种对称性在一定程度上决定了法诺共振的 "手性"[39] （即反射峰出现的波长是比反射倾角更红还是更蓝）。不过，这与正常入射时的选择规则无关，因此可以忽略不计。此外，在最实际的情况下，低折射率基板的存在会打破镜面对称性，只留下面内对称性。由于镜面的加入不必要地增加了模态标签的数量，因此我们将其排除在外。

‍

相反，我们使用模态指数 n 来表示 PCS 模的面外特性。当 n 为奇数（偶数）时，衰变对称性为偶数（奇数），这意味着公式 (3) 中的模式命名方案包含了不对称线形的手性相关信息（注意，即使存在低指数基底，衰变对称性也大致成立）。因此，半无限光子晶体和 PCS 的模式之间存在 1:1 的对应关系： 图 3 和图 4 中的每个模式与 PCS 中的许多模式具有完全相同的面内对称性，根据模态指数的不同，这些模式只有面外的区别 n . 文献[40]描述了 HCG 支持的意外 BIC 与相应一维波导阵列的垂直传播波导模式之间的这种关系。[40]，其中垂直传播模式的往返相位条件预测了 BIC 的色散；在这里，BIC 的整数倍是 2 π 的整数倍，即为模态指数 n .

‍

最后，我们注意到 K 点模式比其他五种高对称性模式更为复杂。特别是 K 点的点对称性为 C 3 v ，如图 2(b) 所示。然而，有两组完全相同的 K 点；图 2（b）中没有画出的那组可以通过对 k y 轴的反射而得到。如图 1 所示，只有在折叠到 Γ 点（如图 5 所示）。对于 K 点的模式，类似的扰动会产生三原子晶格，从而使新的Γ 点的模式数量增加三倍。 Γ 点的模式数量是未扰动单原子晶格的三倍。在扰动的 Γ 点上，源自每组 K K 点将成对混合。混合模式的对称性由直接乘积组描述 C s ⊗ C 3 v ，对应于两组 K 点的关系。这个直积群与群 C 6 v 中的模式命名。 C 6 v . 根据 C 6 v 的模式不一致。 K 点时的模式不一致，但与折叠到 Γ 点并在相关扰动晶格中混合时的模式一致。由于我们的目标是研究扰动晶格中的这些模式，因此在 C 6 v 是更有成效的选择。

‍

选择规则

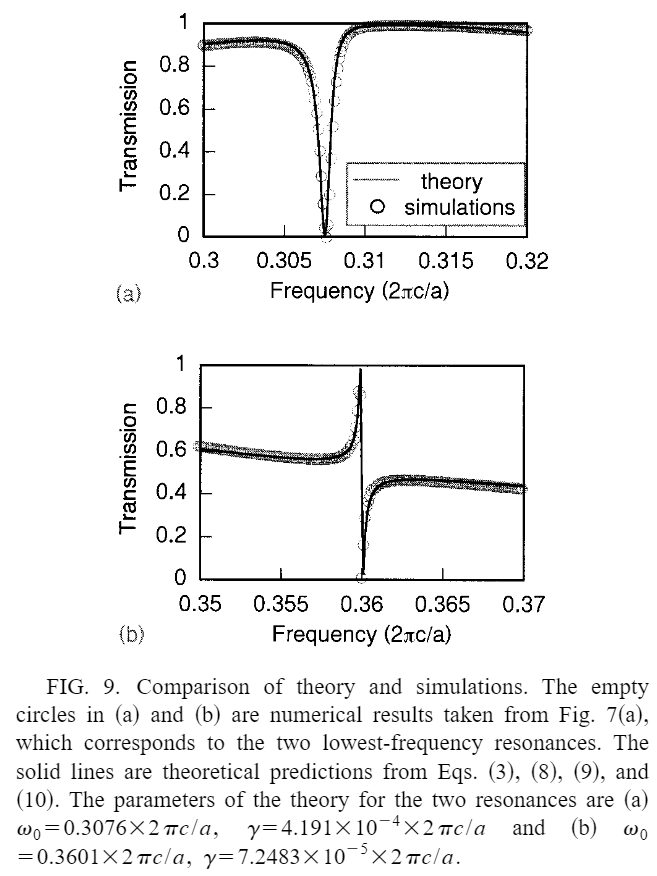
通过适当的周期性扰动，如果满足额外的对称性约束，六类高对称性模式中的任何一类都可以从自由空间进入。这些对称约束可以用群论方法来处理，并产生一个目录，详细说明在给定的平面扰动下，上述每一类高对称性模式如何与自由空间耦合。在下文中，我们将确定针对六种高对称性模式而选择的六种晶格类型（图 5） ，列出与这些晶格类型兼容的所有简并空间群（图 6），然后推导出每种情况下的选择规则（以图 7 和图 8 为例） 。由此得出的目录（图 9 和图 10） 可作为设计平面光子器件的高级路线图。

目标空间群

上述六种高对称性模式产生了六种晶格，每种晶格都针对六种高对称性模式中的一种。对于每一种晶格，我们都会探索出一份通过平面扰动可达到的低对称性晶格的详尽清单。

The symmetry degeneration from higher symmetry to lower symmetry will constrain which polarization, if any, may couple to free space for each high symmetry mode.

从高对称性到低对称性的对称性简并将限制每种高对称性模式与自由空间耦合的偏振（如果有的话）。

图 5 所示的六种晶格类型是根据它们所针对的模式以及它们是以正方形还是六边形对称开始而命名的。 例如，\(Sq_Γ\) 是一种具有方形晶格的单原子光子晶体，其扰动周期与未扰动晶格的周期相同。用 Γ 标记该晶格是因为它不支持连续域中方形晶格支持的其他类型的模式（即 M 和 X 模式） 。图 5（左上）描述了一个真实空间晶格、FBZ 和\(Sq_Γ\)晶格带图的示例。带图中的白色区域是我们所关注的连续域，其中只允许使用第零衍射阶。 我们将自己限制在白色区域的 Γ 点附近区域，在该区域，受对称保护的 BIC 可以产生上述尖锐的光谱特征。

能带图中的白色区域不是光锥，而是第零衍射阶

受对称保护的 BIC 可以产生上述尖锐的光谱特征 是因为 在微扰下，这里变成了QBIC

这种布里渊区折叠也会改变带图中零阶衍射区的形状。[从第二个图知，光锥发生了BZ折叠]

另一方面，Sq M 晶格（图 5 中上部）是一种光子晶体，在单一方向上的扰动周期是未扰动晶格的两倍。这种周期加倍（图 5 中 x 方向）使 k x 方向的 FBZ 范围减半。 然后，新 FBZ 以外的阴影部分通过一个倒数晶格矢量平移到 FBZ 中。结果，未受扰动晶格的 M 点与Γ点重叠，以类似图 1 中例子的方式将 M 点模式带入连续体。这种布里渊区折叠也会改变带图中零阶衍射区的形状。现在，Γ 点既有未受扰动的Γ 点模式，也有未受扰动的 M 点模式。

李师兄说，零阶衍射区就是光锥，零阶衍射区就是个菱形， 0+1+2+.。。。所有衍射区就等于 光锥

将各种高对称点带入连续域：

.图 5 中只有 SqM 晶格将正方形晶格的 M 点模式带入连续体，这也是 SqM 晶格名称的由来。 其余晶格以类似方式针对正方形晶格的 X 模式（SqX，即图 1 中探讨的晶格类型），以及六边形晶格的、M 和 K 点模式（分别为 Hex、HexM 和 HexK）。值得注意的是，在 HexK 晶格的 FBZ 中折叠了两个不同的区域：如上所述，有两组模式折叠到Gamma点上，每组模式来自一个不同的 K 点。

‍

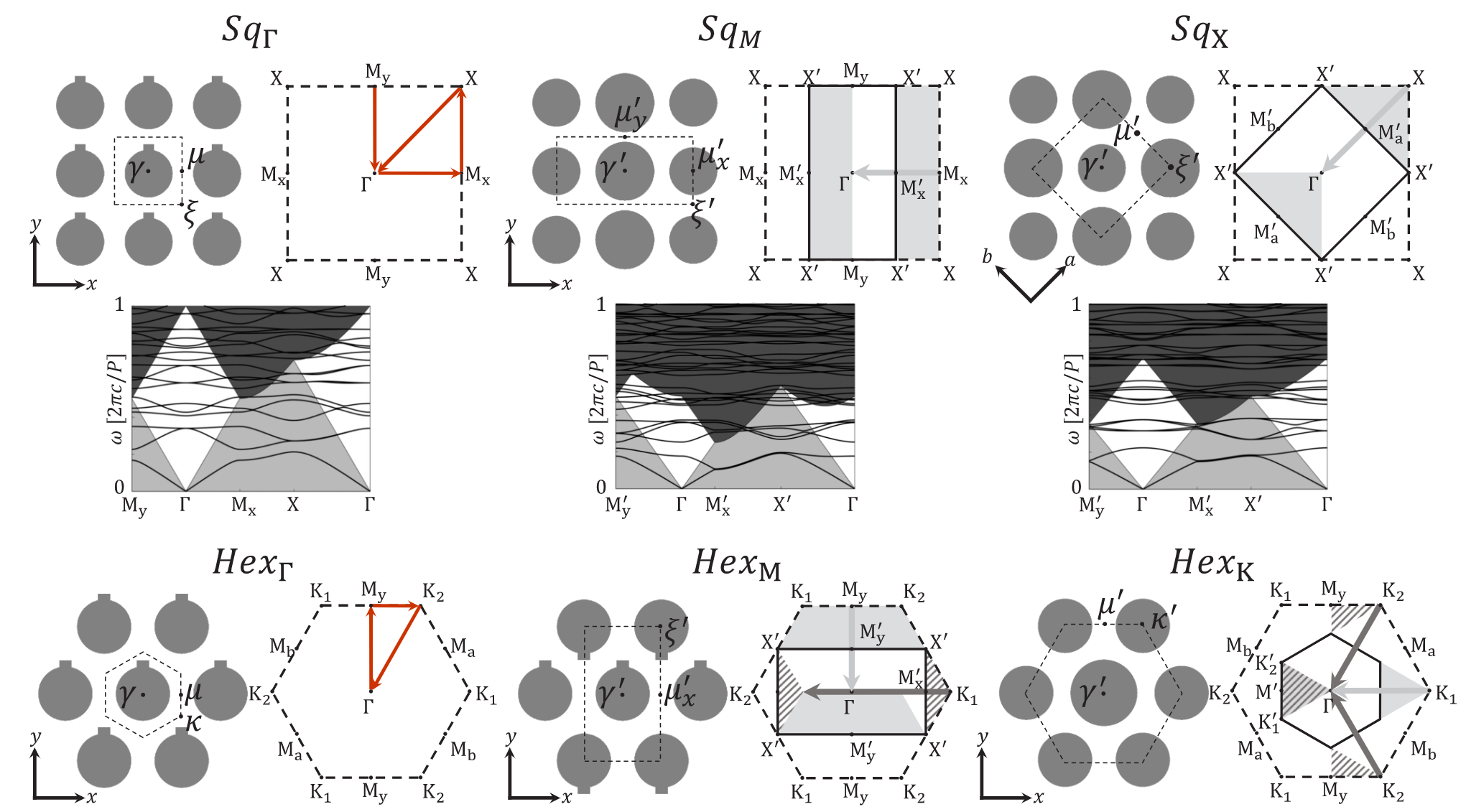
image

image

‍

我们注意到，图 5 中选择的六个网格并不是一个详尽的集合：每个单胞原子数不限的晶格都是可能的。按照每个单胞中的原子数对晶格进行排序，所选的六个晶格是最低阶晶格，它们唯一针对的是我们感兴趣的六种高对称性模式。附录 B 介绍了三个高阶晶格的例子。下文所述方法可用于生成任何高阶晶格的目录。

‍

附录B：一个晶胞中有更多原子的情况：在各个方向上都进行周期加倍,在连续域就可以得到更多的模式（比如X、M、K）

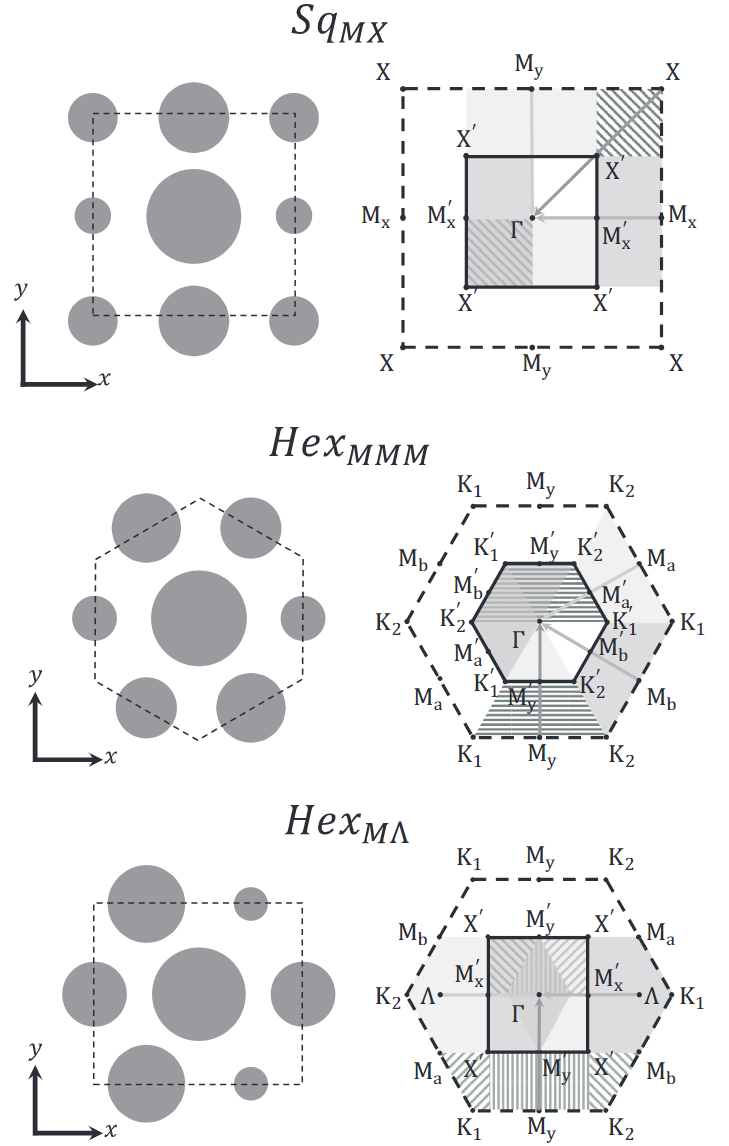
image

这第三个就是Rashba效应的能带折叠的情况的BZ，但是实空间是不一样的

tOvervig-2020-Selection rules for quasibound st.pdf - p25 - his lattice is a “quadromer,” having four atoms per unit cell, and therefore has four times the modes compared to the unperturbed case. I

图 19 所示的晶格绝不是唯一可以探索的其他晶格。 所以我还可以探索一些其他能带折叠的方法

列表中的晶格通常越来越复杂，但如果需要，可以采用第 III 章 C 节中概述的相同方法来确定选择规则。

‍

微扰后的晶格的空间群兼容性表：

‍

首先，列出所有 17 个 "壁纸组"，并按兼容的晶格族（如 "Rectangu-ar"）进行分类。然后，针对每个目标晶格类型（如 SqM）列出与晶格类（即正方形或六边形）兼容的空间群。例如，空间群 p6mm 要求六边形，因此任何方格都不可能是六边形。同样，六边形晶格无法在不扭曲晶格矢量的情况下扰动成正方形晶格，但它可以扰动成矩形晶格。因此，正方形晶格族的空间群在所有六角形晶格中都被省略了，但矩形晶格族的空间群却没有被省略。

idea：矩形BZ可以微扰为六边形BZ 但似乎这就没有谷锁定了

‍

通过这种方法，可以为上述六种晶格类型中的每一种兼容简并空间群生成一个目录。图 9 给出了正方形晶格的目录，图 10 给出了六边形晶格的目录。目录中的一个条目列出了空间群名称、用于描述 V 的点群、V Γ 和 V L 的不可还原表示、简并晶格的可视化示例（使用 "钥匙孔 "图案 [57]），以及扰动晶格中 Γ 点存在的所有模式的选择规则。

选择规则就是图9、10，推导太难，不管

‍

三个六边形晶格族（Hex Γ、Hex M 和 Hex K）的选择规则目录。如图例（右上角）所示，对称性列中的每个条目都指定了空间群、用于描述 V 的点群以及 V 的两个分量的不可还原表示（第一个分量具有未扰动晶格的周期性，第二个分量具有扰动晶格的周期性）。示例栏描述了一个与对称性栏中的规格相符的扰动单元格示例。彩色星形、三角形和椭圆形分别表示具有六倍、三倍和两倍旋转对称性的点。其余各栏分别标为 Γ、M 或 K，并报告了未扰动 FBZ 中相应位置上每种高对称模式的选择规则。行以图例为索引，对应于 FBZ 中以列为标记的点上存在的不同不可还原表征（图例中显示了每行和每列的 TM 模式示例，以供参考）。这些列和行中的条目指的是由于扰动而激发相应模式的自由空间极化，并由给定的坐标轴定义。对于 TM 模式，极化与自由空间电场有关；对于 TE 模式，极化与自由空间磁场有关。空白条目表示禁止激发模式（该模式仍然是受对称保护的 BIC），破折号表示 M 点没有第五或第六个不可还原表示。

‍

应用

上述过程推导出了应用平面内扰动的二维 PCS 的选择规则。由此产生的产品目录分为图 9 和图 10，其中包含大量信息，值得进一步讨论和探索。特别是，目录中的一些独特特征很容易激发设备应用，而这在较简单的一维 PCS 中是不可能实现的。

可以设计出结构紧凑、与偏振无关的设备，如滤波器和调制器。因此，对简并模式的操作具有相当大的技术意义

例如，由于器件的二维性质 ，带状结构可以在两个面内方向上进行优化，从而实现带状结构的全面优化，进而优化器件的结构。一维结构（例如，由矩形光栅指组成的器件，在一个面内方向上不变）可理解为 Sq 𝑀 晶格的一个特例，但对沿光栅指方向的行为控制有限，甚至无法控制。此外，二维结构较高的面内对称性意味着存在简并的 𝐸 -型模式（与正交偏振耦合的特征频率相同的 "伙伴 "模式），这在一维结构中是不存在的。这样就可以设计出结构紧凑、与偏振无关的设备，如滤波器和调制器。因此，对简并模式的操作具有相当大的技术意义。最后，我们注意到目录中高阶空间群和低阶空间群之间的父子关系，并发现通过连续添加不同的父空间群而构建的子空间群，可以实现具有父空间群引入的独立自由度的光学控制。我们证明，这一原理可以控制大量表征光学光谱的参数，远远超过了目前的技术水平。

考虑到这些因素，第四节 A 部分讨论了单原子和多原子 PCS 中存在的简并模式，为使用该目录的偏振无关器件提供了一套全面的选择。第 IV 章 B 节详细介绍了这一讨论所激发的设备应用，证明由三个连续扰动控制的 Hex K 退化基本模式适合通过四波混合产生太赫兹。

证明由三个连续扰动控制的 Hex K 退化基本模式适合通过四波混合产生太赫兹

通过研究目录条目，我们可以发现连续扰动的第二种应用，第四章 C 节展示了可拉伸基底上的 PCS 在实现机械可调光学寿命方面的潜力。最后，第四章 D 节报告了与圆偏振光耦合到 Sq M 晶格的 p 2 空间群相关的几何相位的发现，该相位可与"共振的 Q 因子"同时控制。 然后，我们展示了如何在空间上改变这一几何相位，从而实现一类新颖的光子设备，在这类设备中，出射的法诺共振波面可在空间上进行调整，而非共振光则不受影响。

与圆偏振光耦合到 Sq M 晶格的 p 2 空间群相关的几何相位的发现，该相位可与共振的 Q 因子同时控制。

‍

非局域超表面-几何相位-完全类似Rashba效应！

image

‍

以及如果在空间上改变这种几何相位，我们将如何实现仅在共振时具有反常反射和折射的器件。

前面的应用展示了利用连续扰动来指导设备设计的目录的实用性。换句话说，设计的关键在于理解最终的低阶空间群是如何从高阶空间群中构建出来的，它们共同构成了父子关系。在本节中，我们将对随附论文[64]中的方法进行补充，其中我们将利用这一原理来演示特定的 𝑝 2 空间群是如何从两个父空间群构造出来的。我们阐明了一种几何相位，它是母空间群表现出图 11 所示的那种模式 "扭曲 "的结果，以及如果在空间上改变这种几何相位，我们将如何实现仅在共振时具有反常反射和折射的器件。

我们首先关注 Sq M 晶格中三个空间群之间的关系，如图 14(a)所示。左侧显示的是两个母空间群（p m g 和 p m m）。除了硅柱中心的两倍旋转外，这两个空间群没有共同的对称性。因此，如果连续添加扰动，子空间群将只保留这两倍旋转，形成图 14（a）右侧所示的 p 2 空间群。这个高阶父系和低阶子系之间的父子关系示例非常普遍；Sq M 和 Sq X 晶格的完整层次结构见图 20。(注：附带论文[64]中介绍的多波长元面的层次结构见图 21）。

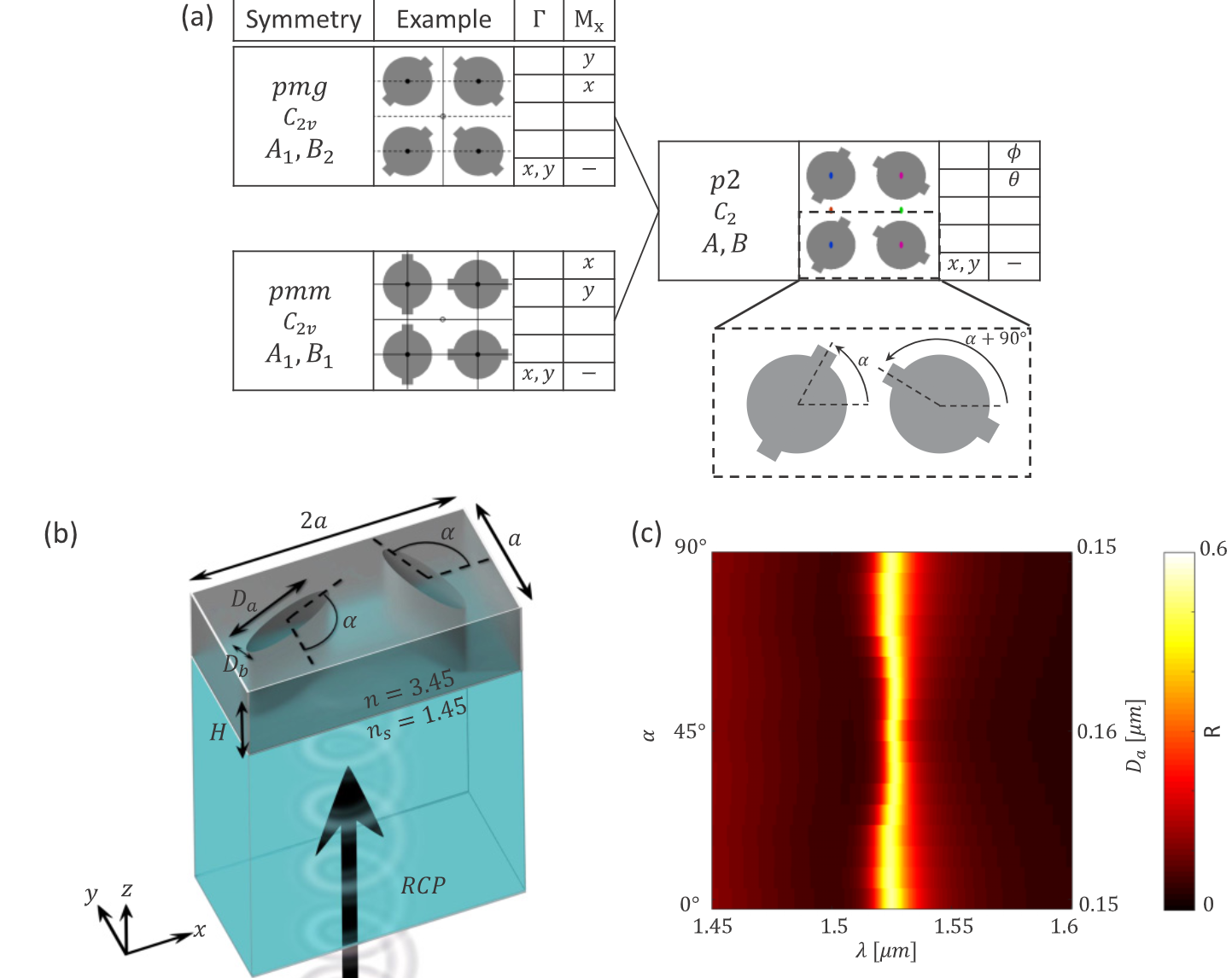
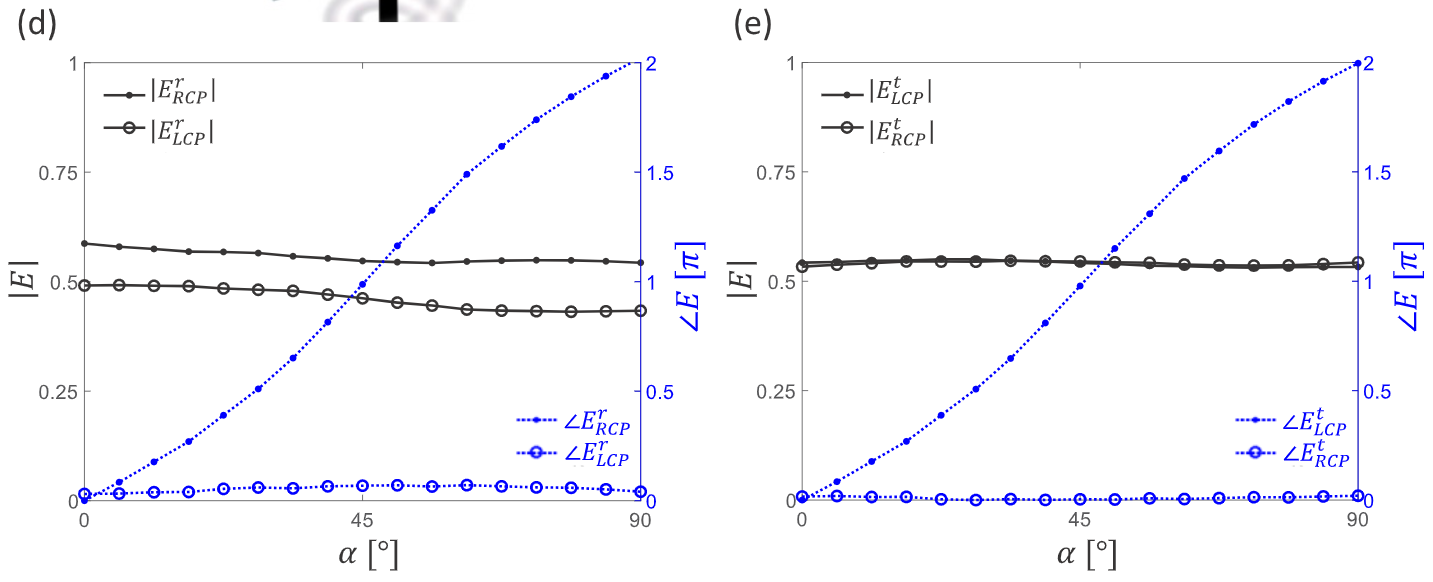image

image图 14：引入两个几何相位因子的元单元。(a) Sq M 晶格中一个 p 2（子）空间群和两个高阶（父）空间群之间的层次关系。(b) 由蚀刻在硅片上的椭圆组成的元单元示意图，由从基底入射的 RCP 光激发。(c) 通过改变 α 和 D a 以保持恒定共振频率而构建的元胞库的反射图reflectance map。 (d) 共振时反射光的 LCP 和 RCP 分量的​振幅和相位响应​。(e) 透射光的 LCP 和 RCP 分量在共振时的​振幅和相位响应。

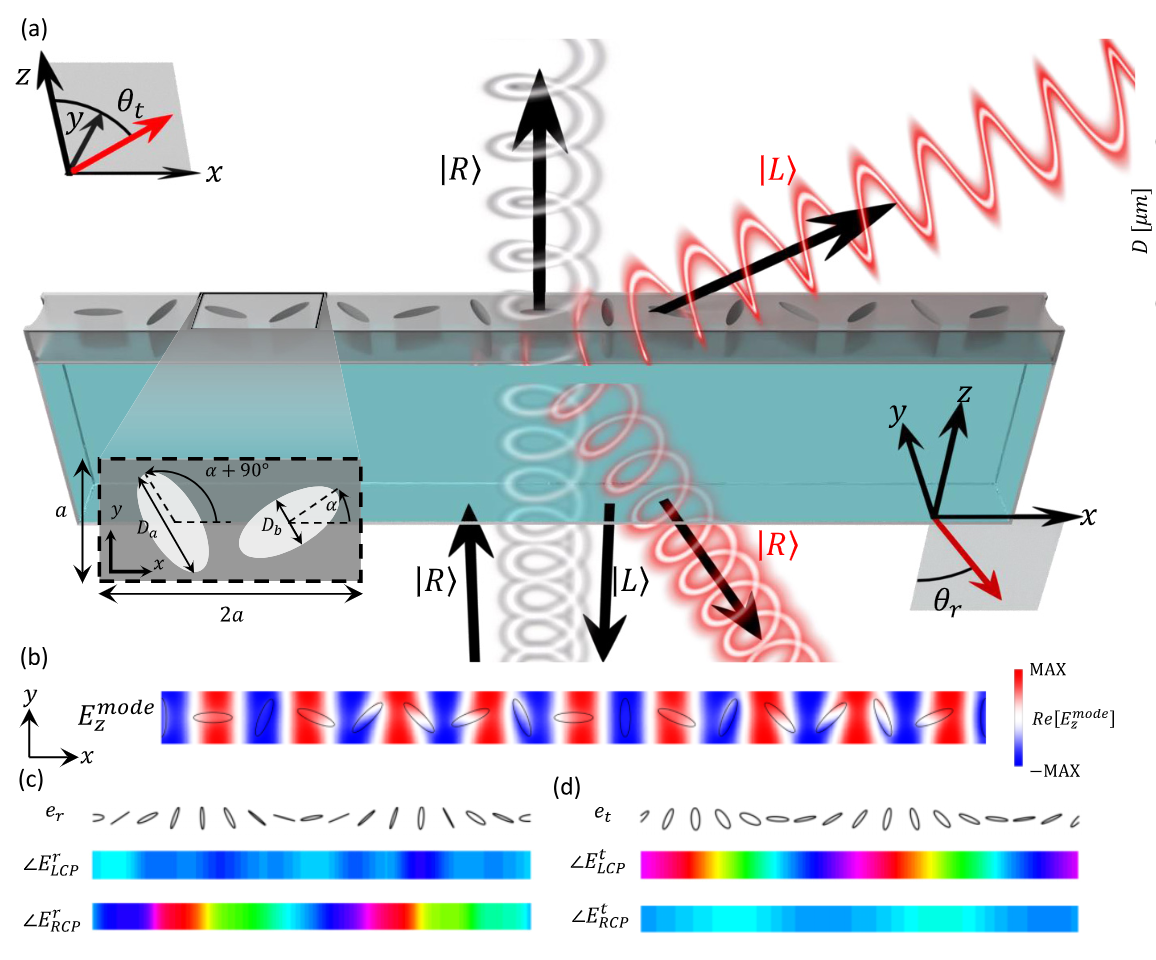
不同的取向角 α，对应的结构能耦合到不同的偏振光！

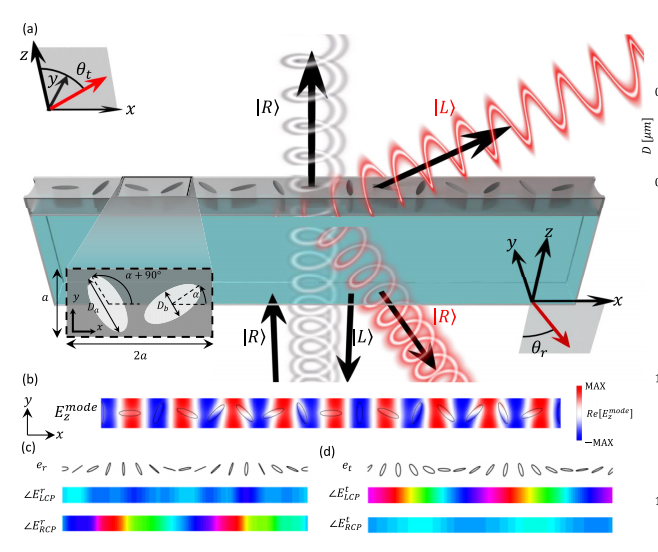
观察图 14(a)可以发现，p m m 母空间群允许耦合到与 x 轴的偏振角 ϕ = 0°（即 x 偏振） ，而 p m g 母空间群允许耦合到与 x 轴的偏振角 ϕ = 90°（即 y 偏振） 。从图 14（a）的插图中可以看出，子空间群可以用取向角 α 进行参数化，当 α = 0 ° 时产生 p m m 母空间群，当 α = 45 ° 时产生 p m g 母空间群。换句话说，当 α 从 0 ° 到 45 ° 连续变化时，相应的偏振角必须从 0 ° 到 90 ° 变化。 这种行为的线性插值为image

这种形式很容易让人联想到著名的几何相位 2 α，当光被沿 α 方向的各向异性散射体散射时，圆偏振的手性发生翻转，就会产生这种相位 2 α。如图 14（b）所示，这种相似性表明在圆偏振光下研究 p 2 空间群。

我以前写过PB相位的笔记

特别是，在研究从器件反射侧和透射侧射出的圆偏振光的相位时，我们发现该系统为转换手性（对于右圆偏振（RCP）入射，在透射中为左圆偏振（LCP）光，在反射中为 RCP 光）的出射光赋予的几何相位是传统几何相位的两倍。 与传统的二色性光学元件（如等离子棒状天线）一样，要分析出射光线，需要偏振基的两个投影，一个是耦合到元件中的投影，另一个是耦合出射光线的投影。我们将依次考虑这两种情况。

右旋圆偏振光打到光子晶体板，在共振波长的输出光（包括透射、反射）是线偏振的。

首先，只有在 ϕ 方向上线偏振的自由空间光分量才能完全耦合到模式中。这部分光（占 RCP 入射光功率的一半）被共振反射，而正交偏振光（角度 θ = ϕ + 90 °）则被传输。将入射的 RCP 光分解为两个线性偏振分量，j 分量的相位为 Φ r 1 = ϕ，θ 分量的相位为 Φ t 1 = ϕ + 90 ° 。由于 ϕ 方向由公式 (28) 中的方向角 α 定义，因此共振反射光的相位为 Φ r 1 = 2 α，正交偏振透射光的相位为 Φ t 1 = 2 α + 90 °。

其次，共振时的输出光为线性偏振光，可分解为 LCP 和 RCP 两部分。这些分量在反射时的几何相位为 Φ r 2 = ∓ ϕ，在透射时的几何相位为 Φ t 2 = ± θ，其中第一个符号对应于 LCP，第二个符号对应于 RCP。最后，我们可以确定反射和透射中 LCP 和 RCP 分量的总相位 Φ = Φ 1 + Φ 2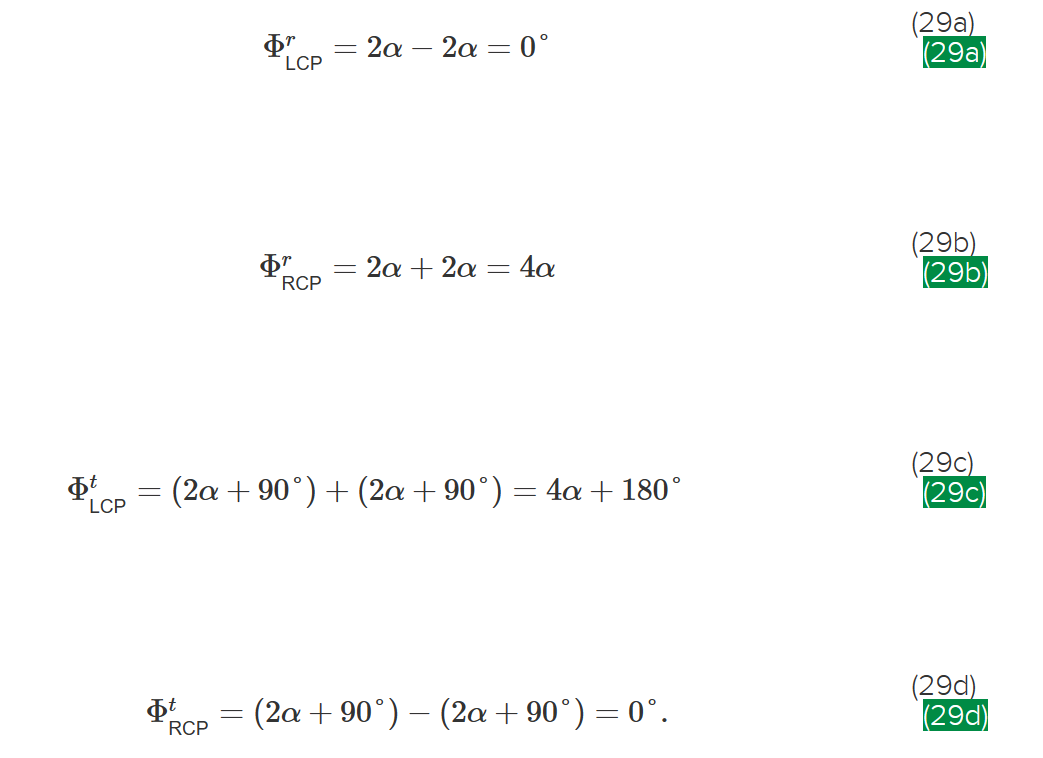：image

虽然出来的是线偏振光，但在反射和透射谱中也可以用波片测量反射和透射谱中的圆偏振分量

也就是说，反射中的 RCP 光和透射中的 LCP 光随 4 α 变化，而反射中的 LCP 光和透射中的 RCP 光对 α 不变。几何相位的两个因子来自偏振态基础变化的两种情况：第一种是从圆形到线性（耦合成单一线性态），第二种是从线性到圆形（分解成其组成的自旋）。在这种情况下，最终值是传统几何相位的两倍，因为与传统的 ϕ = α 情况相比，本征极化（表征投影基础）的变化为 ϕ ≈ 2 α（例如，以 α 角在平面内定向的等离子棒状天线）。我们注意到，ϕ ≈ 2 α 并不是准 BIC 的一般规则；例如，具有十字图案的 Hex K 晶格中的 p 2 空间群的 B 1 模式遵循 ϕ ≈ - 4 α。这导致几何相位为 - 8 α。

我没找到具体微扰方案

接下来，我们将探讨利用这种几何相位作为新自由度的物理学和应用。由于几何相位完全由 α 控制，我们可以利用单元格的其余几何自由度，在具有空间变化几何相位轮廓的设备上保持空间恒定的谐振频率。换句话说，与传统的元表面方法一样，我们可以构建一个几何库（"元单元"），从而实现全相位覆盖和恒定振幅。然后，通过对这些元单元进行空间排列，就可以在谐振频率上实现具有设计相位轮廓的输出波面。

Rashba效应的推广：我们将 D b 保持不变，并改变 D a 和 α，以实现全相位覆盖，同时尽量减少谐振波长的偏移。

为了证实这种方法，我们构建了这样一个以电信波长范围为目标的元单元库。图 14(b)所示的元单元由带有两个蚀刻椭圆的硅片组成，这两个椭圆完全相同，只是旋转了 90°。选择的硅片厚度为 H = 250 nm，晶格常数为 a = 400nm。为构建元单元库而改变的平面内几何参数是沿半主轴 D a 和半次轴 D b 的直径以及取向角 α。为简单起见，我们将 D b 保持不变，并改变 D a 和 α，以实现全相位覆盖，同时尽量减少谐振波长的偏移。

图 14（c）显示了通过全波模拟计算的反射率光谱图，说明整个元单元库的谐振波长接近恒定。 图 14(d) [图 14(e)]记录了工作波长 λ op = 1.52 μ m 时反射（透射）的 LCP 和 RCP 分量的振幅和相位。LCP 和 RCP 分量的振幅大致相等（各约占输入功率的四分之一），并且在元单元库中变化很小。这种微小的不平等是由于基底的存在打破了平面外方向的对称性。

这里透射谱的计算应该与 02年导模共振论文中的一样，是先用白光入射吧，然后看透射或反射谱中 共振波长 ，分解为左旋和右旋圆偏振光的叠加

[image 45ZE [1]0.5isLE icpO LERcpiioibipioioiotiptpotototiot中…作90a °] 图 14：引入两个几何相位因子的元单元。(a)....

当 α 在 90 ° 范围内变化时，具有转换手性的分量（对于反射是 RCP，对于透射是 LCP）的相位在 2 π 范围内变化，并且与预测的 Φ = 4 α 依赖性密切相关[见图 14(d) 和 14(e)]。

这是因为从图中知，由于\(\alpha\)是从0到90，所以从Φ = 4 α知，Φ是从0到360

此关系式见(29)式

‍

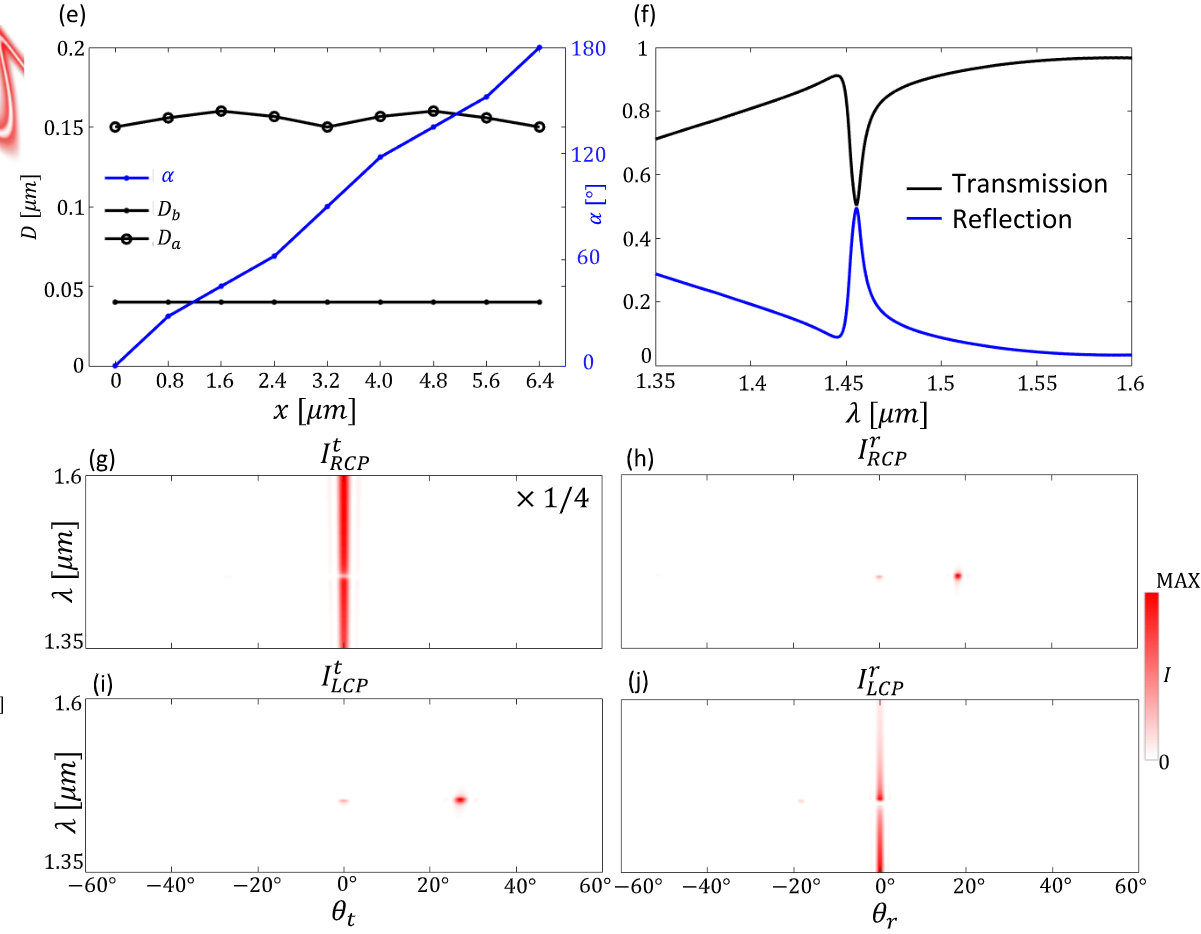
有了元单元库，就可以在 λ op 附近的窄带宽内实现具有空间形状相位轮廓的波阵面。一个常见的功能是线性改变输出相位，从而产生反常的反射和折射。我们可以选择在与二聚化相同的方向（图 14(b) 中的 x 方向）或正交方向上改变相位轮廓。我们将从前者开始（后者见相关论文[64]）。

图 15(a)显示了器件偏转的示意图，该器件在共振波长处对通常从基底侧入射的 RCP 光进行了手性转换。 图 15(b)描述了全波模拟计算出的共振电场，并与器件的几何形状相叠加[图 15(e)]。图 15(c) 和 15(d) 分别显示了 LCP 和 RCP 分量在反射侧和传输侧的输出极化状态和相位。在这两种情况下，整个器件的输出极化近似线性。因此，未转换手性信号的相位是均匀的，而转换手性信号的相位则随着 α 在 180 ° 上的变化而在 4 π 上变化。

图 15(f)证实，尽管整个元面的几何形状存在差异，但元面的共振仍然完好无损。不过，与最初选择的 λ op 相比，出现了明显的蓝移。尽管如此，在器件的谐振峰 λ dev = 1.46 μ m 处，手性转换后的信号仍会偏转到第二衍射阶[图 15(g)-15(j)] 。附带论文[64]显示了一个具有相同偏转角的装置，但在二聚化方向的正交方向上施加了相位梯度。在这种情况下，蓝移也会出现，但会明显减少。

image梯度共振元表面。(a) 设备及其功能示意图：在石英表面的硅薄膜上刻有椭圆形孔（插图显示了几何形状的俯视图），在圆偏振光的激发下，共振偏转转换手性的光。.(b) 梯度共振元表面上叠加的共振复场俯视图。(c)、(d) 反射和透射偏振态（er 和 et）的空间分布俯视图，以及 E rRCP、E tRCP、E rLCP 和 E tLCP 的相位响应。 (e)(b)中装置的几何参数。(f) (b) 中装置的透射和反射光谱。(g)-(j) 根据光学近场计算出的远场角分布和光谱强度分布，如(c)、(d)中的结果。

image

‍

对这种蓝移现象的解释来自于这个元表面的一个独特特征：转换手性的光偏转是由设备的超模式介导的。也就是说，与传统的元表面（其元单元基于局部共振散射光线）不同，这种元表面由于许多相邻元单元支持的全局共振（与超模式相关）而散射光线。为了探索其中的物理原理，我们考虑了梯度共振元表面对 RCP 光入射角的依赖性。图 16(a) 展示了一个在与二聚化方向正交的方向上具有空间相位梯度的器件，光线以一组角度 θ x（沿相位梯度）和 θ y（沿二聚化方向）从基底入射。由于偏转只发生在共振时，因此共振频率遵循某种色散关系（即带状结构）。图 16(b) 描述了当 θ y 在 - 40 ° 至 40 °（根据斯涅耳定律，相当于空气中的± 68.7 °）之间变化时的共振频率色散。该模式是向上凹的，这意味着在较高的面内矩时，会发生蓝移。

‍

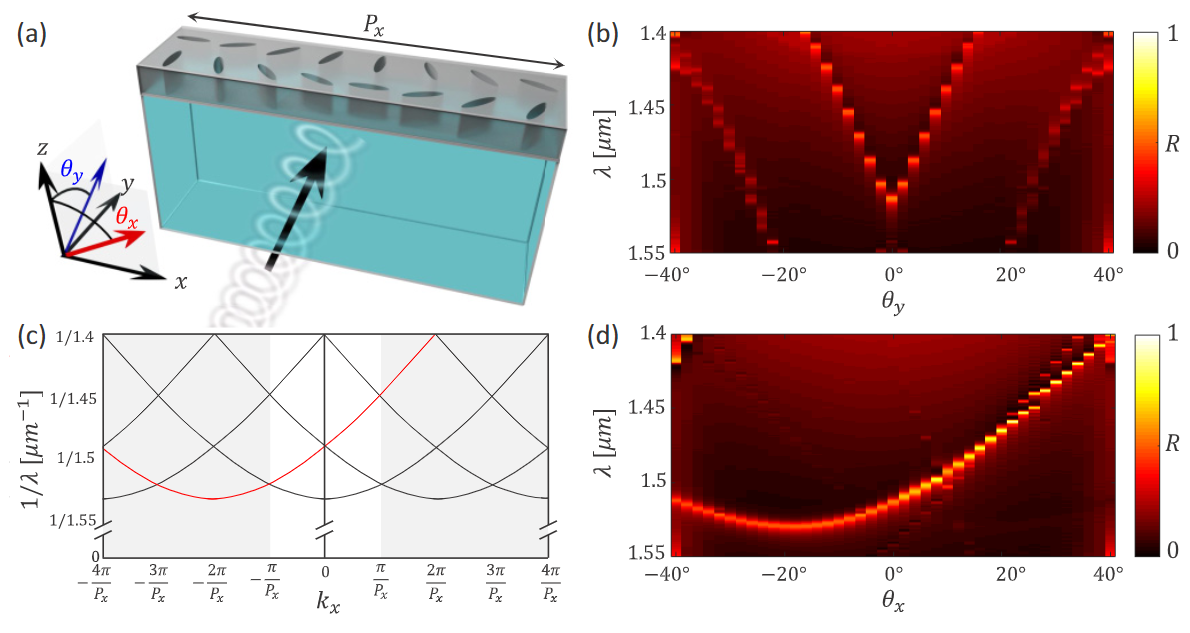image图 16.共振元面的角色散。(a) 从偏离法线角度激发的共振超表面示意图。(b) 改变 θy 时的反射率图，显示共振跟随模式的色散凹上带。 (c) (a) 中装置共振附近的扩展区（灰色阴影）带状图，带状图中有人工布里渊区折叠；Overvig-2020-Selection rules for quasibound st.pdf - p22 - the red band corresponds to the band shifted by a k vector equal and opposite to that introduced by the phase gradient due to coupling into the supermode (i.e., one factor of the geometric phase).红色带状图对应于因耦合到超模式（即几何相位的一个因子）而产生的相位梯度所引入的与之相等且相反的 k 值移动的带状图、(d)改变 θx 时的反射率图，显示共振随几何相位梯度因子移动的频带。

‍

‍

通过构建元单元库，可以在 λ op 附近的窄带宽内实现具有空间形状相位轮廓的波阵面。一个常见的功能是线性改变输出相位，从而产生反常的反射和折射。我们可以选择在与二聚化相同的方向（图 14(b) 中的 x 方向）或正交方向上改变相位轮廓。我们将从前者开始（后者见相关论文[64]）。

图 15(a)显示了器件偏转的示意图，该器件在共振波长处对通常从基底侧入射的 RCP 光进行了手性转换。图 15(b)描述了全波模拟计算出的共振电场，并与器件的几何形状相叠加[图 15(e)]。图 15(c) 和 15(d) 分别显示了 LCP 和 RCP 分量在反射侧和传输侧的输出极化状态和相位。在这两种情况下，整个器件的输出极化近似线性。因此，未转换手性信号的相位是均匀的，而转换手性信号的相位则随着 α 在 180 ° 上的变化而在 4 π 上变化。

要理解法线入射时的蓝移现象，我们必须考虑：（1）器件支持的模式；（2）共振模式的面内动量。首先，这些谐振模式在相位梯度方向上的超周期为 P x = 8 a。因此，我们考虑了具有该超周期的器件所支持的所有超模。由于超周期是由同一 PCS 的扰动版本组成的，因此超模可以通过人工布里渊折叠很好地近似，这相当于将一个元单元的周期加倍三次。图 16(c)描述了有关模式的这一过程，显示了在 k x = k 0 sin ( θ x ) 方向上复制了光栅矢量 k G = 2 π / P x 的每一个整数倍的单位单元带（包含两个椭圆）。图中 k x = 0 处的超模就是正常入射时的超模。

就是Rashba矢量：

其次，在耦合时，存在一个空间变化的几何相位，相当于椭圆局部旋转角的两倍。这个空间相位的导数相当于 k 向量、image

换句话说，共振超模是未受扰动晶格的共振模式，由 x 方向的平面波矢量调制。这对应于距离未扰动 Γ 点 k x = 0（波段的平坦部分）k geo 的超模。图 16(c)中用红色标出了超模。 因此，如图 16(d)所示，随着 θ x 的变化，共振会沿着未扰动晶格中存在的频带色散方向移动 - k geo。值得注意的是，这也意味着与一对入射矩 k x = 0 和 k x = - 2 k geo 相对应的共振频率是相同的。 这符合互易性的要求：这两个力矩是偏转过程的输入和输出力矩；反转输出必须在所有频率上产生原始输入。

最后，我们对受角位散限制的可实现相位梯度进行评论。如公式 (2) 所示，共振涉及的分量 k 向量必须根据共振的线宽和角色散加以限制，以保持较大的共振可见度。对于塑造入射平面波的共振元面透镜或全息图，输出 k 向量的范围必须满足公式 (2)。在随附论文[64]中报道的圆柱形元面透镜中，尽管整个器件在 θ x 方向上的偏转角范围很大，但共振可见度仍能保持，这可以用数值孔径 NA 来表征。我们发现，增大 NA 会逐渐降低共振可见度，但在 NA = 0.7 的高值下，仍能保持较高的共振可见度（峰值反射率大于 40%）。但对于在 θ y 方向聚焦的圆柱透镜，NA < 0.1 是保持可观共振可见度的必要条件，因为与 θ x 方向相比，θ y 方向的角散很大[比较图 16(b) 和图 16(d)]。这与公式（2）对 Q 因子、频带平坦度和入射 k 向量扩散的限制是一致的。换句话说，这表明通过带状结构工程，可以实现完全径向聚焦的共振元面透镜，而且我们通常必须在应用扰动之前注意对未扰动共振元面的带状结构进行工程设计，正如第二章 A 节所述的三步过程所规定的那样。

鉴于非谐振光波不受影响，无论入射角度如何，都能高效传输，我们预计这些谐振偏转和聚焦元表面对增强现实显示器具有重大意义，因为增强现实显示器旨在将所需图像叠加到通过玻璃传输的来自外部世界的信息之上。通过进一步应用连续扰动原理，我们在随附论文[64]中表明，单波长谐振元表面可以扩展到具有独立可调相位轮廓的多波长设备。图 21 显示了由八个父空间组构建的子空间组的层次结构。八个父波代表了入射波面空间和光谱形状的八个自由度：可以同时控制具有不同对称性的四种模式的 Q 因子和偏振角（即几何相位）。值得注意的是，这八个自由度是对未扰动晶格中存在的自由度的补充，未扰动晶格可用于控制所需模式的共振频率和波段曲率。这种对光学光谱的空间和光谱控制程度大大超越了目前的技术水平，只要结合连续扰动的设计原理仔细研究产品目录，就能一目了然。

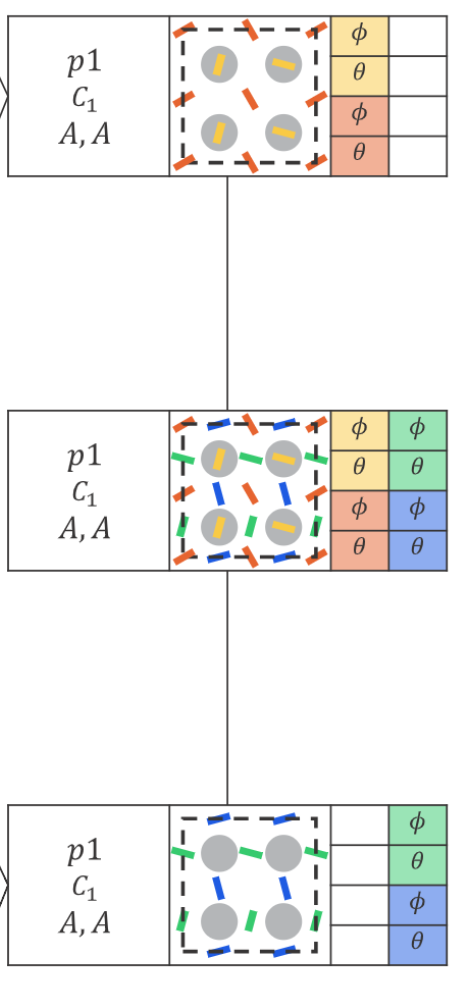image图 21.通过 C2 v 点对称和 "正交 "选择规则添加八个空间群的完整层次结构，最终形成具有八个自由度的 p1 空间群：四个不同模式的 Q 因子和极化角。

Phys. Rev. Lett. 125, 017402 (2020) - Multifunctional Nonlocal Metasurfaces (aps.org)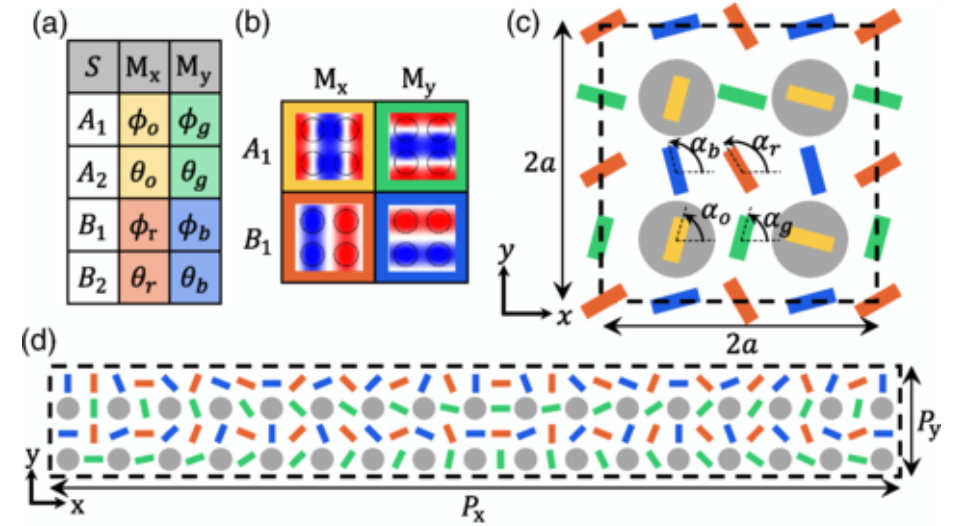image

特别注意，d图是同一个颜色的砖块在不断变化！

‍

‍

  1. 02年Fan-2002-Analysis of guided resonances in photonic crystal slabs

    导模共振的频率与kx之间的关系：图10

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402205052-spe9lmg "We determine the position and width of the resonances by Fourier transforming the decaying tail, as discussed earlier in Sec. III C. The results are summarized in Fig. 10, where we show the frequencies of the resonances as a function of k x ">>

    ‍

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402151548-6qdyn9u "In most cases, the line shapes for these resonances are asymmetric and rather complicated.">> 太复杂了！

    为什么说这些尖锐的共振特征是反对称的？可能是因为图7中，有的透射率是1，有的是0

    尖锐的共振特征来源于光子晶体板的GMR

    Fan-2002-Analysis of guided resonances in phot.pdf

    共振的含义就是：在光锥内,发光、辐射。

    ‍

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401155221-amcfzm3 "we calculate the dispersion diagrams, the modal patterns, and transmission and reflection spectra of these resonances">>

    在这一过程中，出现了一个重要的观察结果，即传输和反射过程存在两条时间路径。

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401155343-en2gc6k " introduce a general physical model that explains the essential features of complex spectral properties.">>

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401155508-y0t2ipg "the quality factors of these resonances are strongly influenced by the symmetry of the modes and the strength of the index modulation.">>

    引言

    guided mode

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401155800-93o9wdz " These structures support in-plane guided modes that are completely confined by the slab without any coupling to external radiations.">>

    在波长尺度上控制光：<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401155845-be8dcfe "These guided modes allow control of light within the layer at the wavelength scale.">>

    ‍

    guided mode resonance

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401160150-lokbo3o "Similar to the guided mode, a guided resonance also has its electromagnetic power strongly confined within the slab. ">>电磁功率强烈限制在板中。
    可以与外部辐射耦合、可以耦合到外部环境

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401160711-65pnrle "the resonance can couple to external radiation">>. <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401160818-a1qw0zd " guided resonances can provide an efficient way to channel light from within the slab to the external environment. ">>

    GMR的应用：激光、单向耦合器、滤波

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401160950-kzbx8da "This property has been exploited in designs of novel photonic-crystal-based light-emitting diodes,11,16lasers,17,18 and directional output couplers.19 In addition, the guided resonances can significantly affect the transmission and reflection of externally incident light, resulting in complex resonant line shapes that are useful in filter applications.9,20">>

    ‍

    本文的目的：

    计算了GMR的能带图、本征场分布

    使用FDTD（时域有限差分仿真）计算透射和反射谱，从而实时地可视化GMR与入射光的相互作用。

    发现：<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401163348-ncdotey "the presence of two temporal pathways in the transmission and reflection processes.">>

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401163548-se50l9b "uses only interference and energy conservation arguments, to explain all the complex features in the spectral lineshapes.">>

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401163628-iytapha " angular and structural dependences of the guided resonances">>

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401163646-ai800tw "wide ranges of tunability in quality factors for these resonances.">>

    GMR的能带结构

    由于光子晶体板中GMR的光谱特征（透射谱、反射谱）将主要取决于它们的模态特性，因此在开始讨论时简要介绍一下这些共振的带状结构特性是很有帮助的。

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401164043-01wttnh "Fan-2002-Analysis of guided resonances in phot-P1-20240401164043">>
    ​image<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401164201-t842x80 "The thickness of the slab is 0.5a, and the radius of the holes is 0.2a, where a is the lattice constant. The dielectric constant of slab is 12, which roughly corresponds to the dielectric constant of Si or GaAs at optical wavelengths.">>

    ‍

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401164453-wsdplqw "Fan-2002-Analysis of guided resonances in phot-P2-20240401164453">>
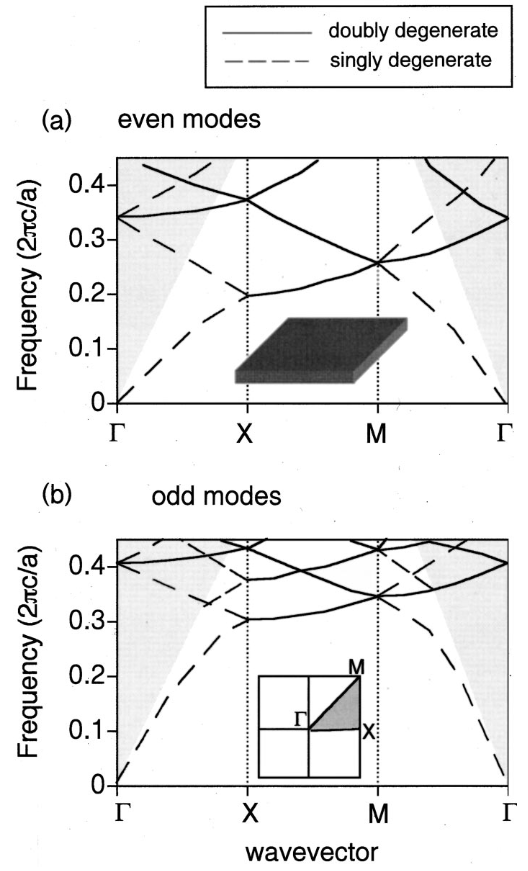    ​image图 2.均匀介质板中偶和奇模式的带状结构。板厚度为 0.5a，介电常数为 12。假定晶格为方形晶格，晶格常数为 a。 这里的线条是导频模式。实线代表双退化态，虚线代表单退化态。. The gray regions are the continuum of radiation modes.

    均匀介质板

    为了了解光子晶体板中不同类型模式的起源，让我们首先简要回顾一下均匀介质板的带图。为此，我们考虑厚度为 0.5a、介电常数为 12 的均匀板。图 2 中绘制了这种结构的带图。在此，我们使用简化区方案展示带图，假设晶格为方形，晶格常数为 a。The lines here correspond to the guided modes that are confined within the slab, while the gray region corresponds to the continuum of radiation modes. Radiation modes lie above the light line, which is defined as the boundary of the gray region.

    对GM分类为奇和偶模：是根据：见光子晶体书108页，偶模就是类TE模，奇模就是类TM模

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401171952-4eiyz6z ". We separate the guided modes into even or odd modes, characterized with respect to the mirror plane parallel to the slab.">>

    .由于使用了缩减区方案（即只考虑第一BZ），一些导模存在于光线之上。然而，由于结构的潜在的连续平移对称性，这些模式不会与辐射模式耦合。 此外，我们还注意到在许多 k 点存在双重退化带，在 Gamma 点出现了四重退化

    在光子晶体书中，一个玻璃板也有能带

    这个可以类似从Rashba效应那篇论文能带折叠来理解，本来光锥外的模式，由于能带折叠，相差一个倒格矢，就折叠到光锥之上了

    但为什么不会耦合到辐射模式？

    • 也许是因为倒格矢是任意的，所以光锥之上的模式可以平移倒格矢，从而移动到光锥之下？
    偶模和奇模的含义：光子晶体书100页图4就可以理解，还有102页！

    image

    ‍

    光子晶体板

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240401173626-2aqmm26 "Fan-2002-Analysis of guided resonances in phot-P2-20240401173626">>
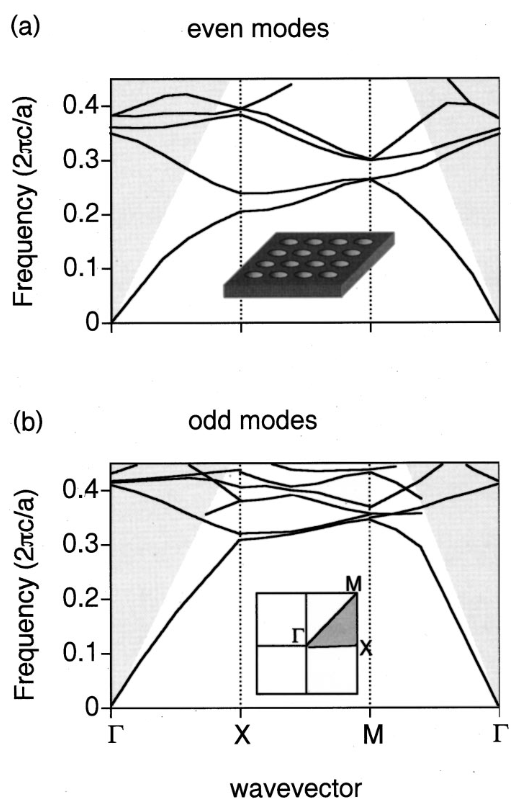
    ​image

    与均匀介质板的能带图相比，光子晶体板结构的能带图显示出重要的异同点。对于图 1 所示的模型系统，偶模和奇模的带图分别绘制在图 3​a 和图 3​b 中。光线以下的模式仍然是真正的导波模式，具有无限的寿命，尽管气孔引入了较大的折射率对比度。

    光锥之上的导模可以与辐射辐射模式耦合，并拥有有限的寿命，这种模式称为导模共振

    另一方面，光线上方的导波模式现在可以与辐射模式耦合，并拥有有限的寿命。 因此，这些模式成为导模共振。它们之所以被称为 "导模"，是因为它们与均匀板中的导模能带密切相关，因此应在介质板中保留了重要的电磁功率部分。

    辐射模式是什么？

    ‍

    ‍

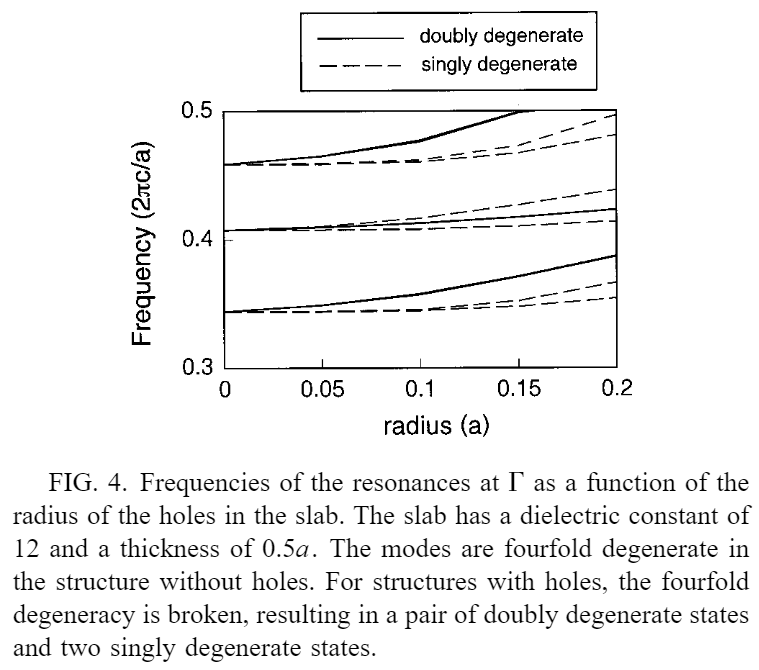
    晶体中气孔的存在也降低了晶体结构的平移对称性，使其从连续对称性变为离散对称性，从而降低了晶带的简并。除了特殊的 G、X 和 M 点之外，在大多数 k 个点上，带现在都是单简并的。 在 Gamma 点，点群支持二维不可约表示，允许存在双简并态。因此，均匀板在 Gamma 点的四重简并在气孔存在的情况下会分裂，如图 4 所示，我们在图 4 中绘制了 Gamma 点共振频率与气孔半径的函数关系。随着空穴半径的增大，模式会分离成一对双简并态和两个单简并态。

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402112319-27v9o8a "Fan-2002-Analysis of guided resonances in phot-P3-20240402112319">>
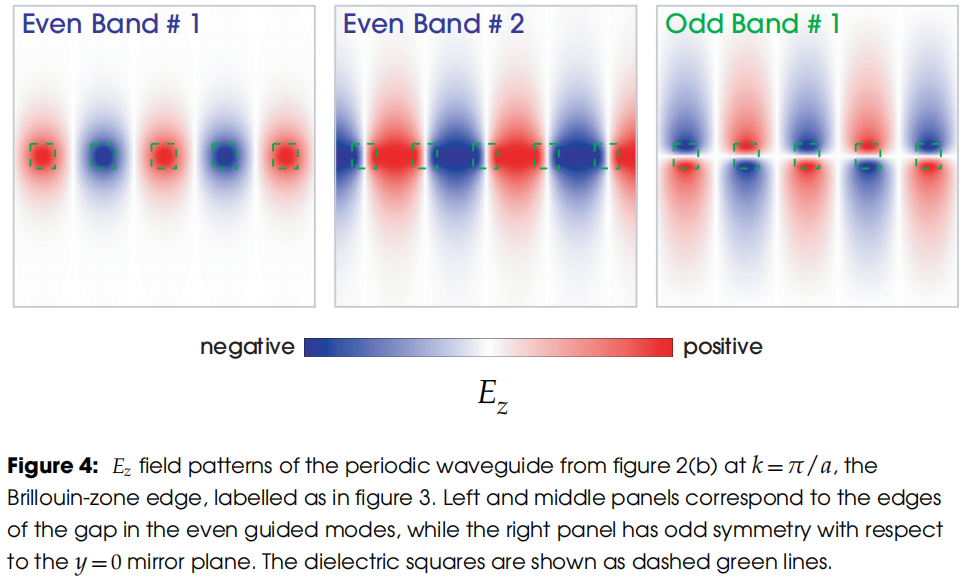
    ​image

    Gamma 处第一个导模共振带的功率密度分布：图 5b 也显示了该模式的共振特性，即​功率密度被强烈限制在板内。

    对于 r=0.20a 的晶体结构，我们在图 5 中显示了 Gamma 处第一个导模共振带的功率密度分布。该模式为单简并模式，频率为 $\omega=$0.353x2 \(\pi\)c/a。由于任何单简并模式都应属于一维不可约表示，因此该模式的功率密度分布应具有晶格的完全对称性。从图 5a 可以看出这一点，图 5a 显示了功率密度在平行于板的切片上的空间分布。

    此外，图 5b 也显示了该模式的共振特性，即功率密度被强烈限制在板内。

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402113406-aa1kru7 "Fan-2002-Analysis of guided resonances in phot-P3-20240402113406">>
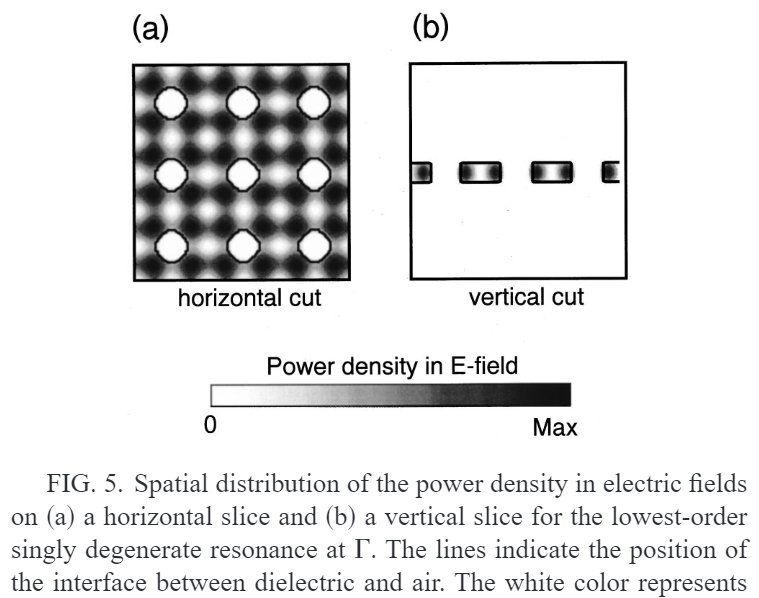
    ​image

    一个问题：上面fig5b中，垂直切面图中显示电场能量局域在板中，而外面空气中几乎没有场，这是正确的吗？答案：实际上这里图5b画的是对的，板子外面实际上是有辐射的，只不过因为板内的电磁能量太强了，所以光子晶体板外面的平面波的强度看上去太弱，显示的是白色。实际上,利用comsol计算周期结构本征频率(comsol软件是会考虑kz的)，在光锥之上的模式，通过调节颜色对比度,就可以发现空气中也是有电磁能量的，而且是倾斜的（即有发射角），彭超那些UGR的论文也是这样。

    在Rashba效应中，能带折叠到光锥之内的两个点，与光锥之外的两个点相比，z方向切面看上去都是相同的，并没有因为折叠到光锥之内，就发生了什么区别：image、image、image【Hz、normE都是这样】
    但是若手动控制colorbar，看Ex，就可以看出是辐射的波有方向性的：imageimageimage

    对Rashba效应来说，我们关注的应该是新的BZ中的模式，而不是原来的K点

    ‍

    ‍

    因此，通过带状结构计算，我们可以研究导模共振的色散、场分布和对称特性。为了全面了解这些共振，我们还必须研究它们的寿命及其与外部辐射的相互作用。 这些问题将在下一环节中通过有限差分时域模拟来解决。

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402113604-6o3e2aj "III. TIME-DOMAIN ANALYSIS OF THE GUIDED RESONANCES">>

    计算方法

    透射和反射谱的FDTD计算方法：

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402114213-kgmbf2m "Fan-2002-Analysis of guided resonances in phot-P3-20240402114213">>
    ​image​<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402113813-6v0x88m "The computational domain encloses a single unit cell of the crystal">>

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402114122-t8qavac "A plane of dipole sources generates the incident plane waves. ">> <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402114158-rgdo11x "transmitted and reflected amplitudes are determined by recording the fields at the monitor points positioned at both sides of the structure.">>

    ‍

    布洛赫周期边界条件（floquet周期边界条件）

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402114542-90kb7i1 "Fan-2002-Analysis of guided resonances in phot-P3-20240402114542">>

    image

    ‍

    源平面产生了一个具有平行波矢量分量 k 的入射平面波

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402114910-gkb397w "For two dipoles in the plane that are separated by a distance vector r, we set the relative phase between them to be e i(k"r) .">>因此，结合公式 ~1 中规定的边界条件，源平面产生了一个具有平行波矢量分量 k 的入射平面波（从平面波公式的表达式知确实）。此外，偶极矩的振幅被设置为​<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402115139-j21nyk7 "oscillate at a constant frequency with a Gaussian profile to create a temporal pulse">>。具有恒定频率，但其实频率是具有高斯外形的！李师兄告诉过我FDTD中的设置。是一个白光平面波，此白光平面波的中间频率就是这里说的"恒定频率"，从图7中看，可能就是0.4？。

    ‍

    注意这个论文中说的<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402115537-dk5wa6n "a parallel wave vector component k.">> \(\mathbf{k}\)指的是平行波矢！

    在计算中，通过改变频率，其实就是改变了入射角：

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402120457-30ld9tv " This computational setup thus allows us to calculate the response functions of the structure at a given k for a wide range of frequencies in a single simulation run. ~Notice that this is not a constant incidence angle calculation. At a fixed parallel wave vector k, the incidence angle changes with frequency.!">>

    因为平面波满足\(\omega=kc\)

    ‍

    反射和透射光谱的获得：

    首先对各自监测点记录的场幅时间序列进行傅里叶变换，即可获得透射和反射光谱。（我们注意到，仅在两个监测点监测场幅，对于没有衍射发生的频率范围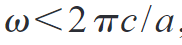image 是有效的。【衍射就是绕射】 ）然后根据入射脉冲对光谱进行归一化处理，入射脉冲是在真空中进行的相同模拟计算，没有光子晶体板状结构。对于反射，归一化步骤之前要减去入射脉冲。

    对时间域的波列进行傅里叶变换，得到的就是频率，而不是波矢。见物理光学书67页。

    ‍

    B. Transmission and reflection spectra

    谱的特征：光谱由叠加在平滑变化背景上的尖锐共振特征组成。

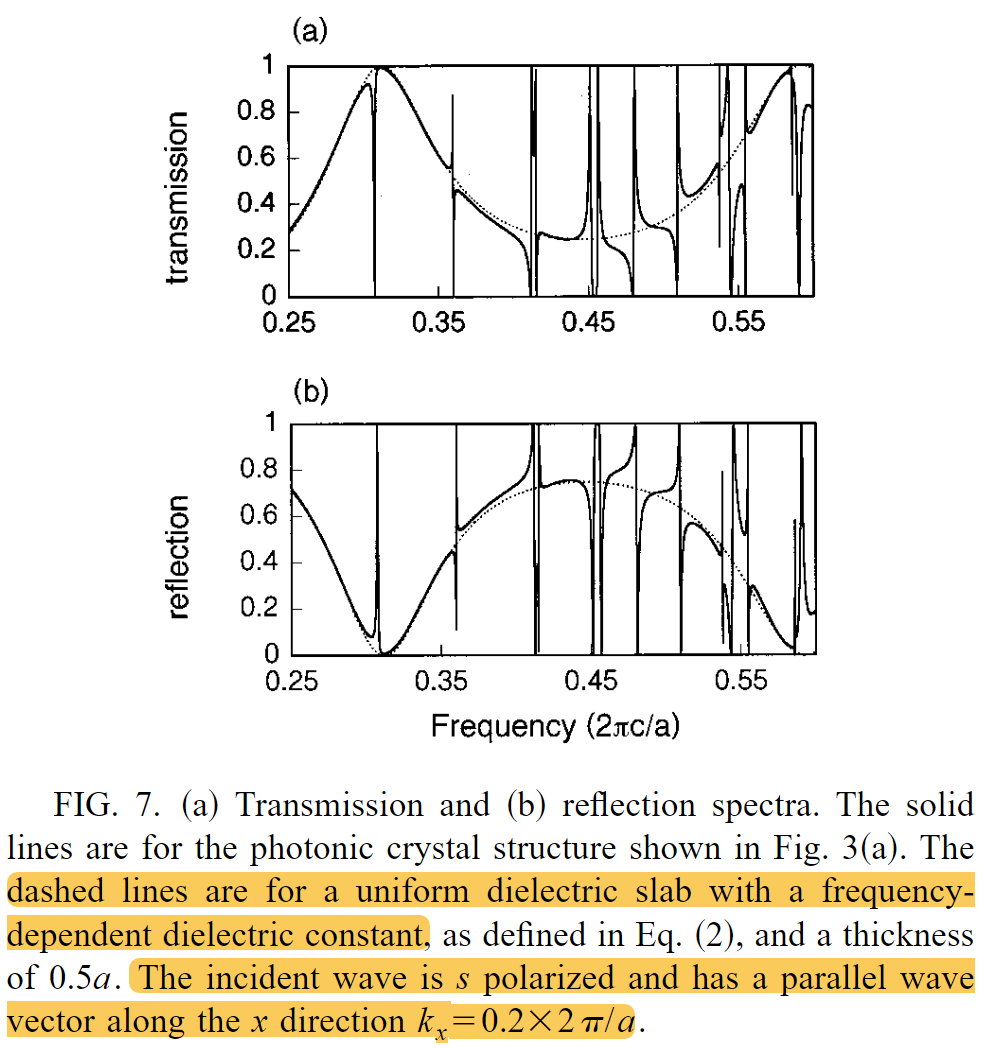    image​，s极化指的是电场垂直于纸面向外：<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402123320-gzmpnow "~An s-polarized wave has its electric field perpendicular to the plane of incidence. In this case, the electric field is polarized along the y direction.!">>

    image对应图4

    ‍

    透射和反射谱中的背景是：均匀介质板

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402143200-fgf9uha ", we fit the background to the spectra of auniform slab, which are shown as dashed lines in Fig. 7.">>

    从此背景可以获得有效介电常数\(\varepsilon_1\)

    \(\varepsilon_1\)​<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402143847-rl967lf " ́1 is a slowly varying function of the frequency.">>

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402143924-gt9judg " At low frequencies, the wavelength of incident light is large, and ́1 for this polarization approaches the average dielectric constant ́">>​\(\varepsilon_{avg}\)

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402144213-qq9as5s " At higher frequencies,">> \(\varepsilon_1\)​<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402144229-j5l1c5h " ́1 starts to deviate from ́avg . Within the frequency range in Fig. 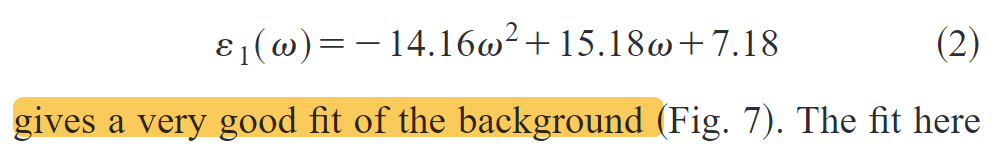7, ">> <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402144312-w3026n2 " we have found that a frequency-dependent dielectric constant">>image

    总之，除了尖锐的共振特征外，光子晶体的光谱背景可以通过使用频率相关介电函数的均匀介质板模型来充分解释。

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402151132-a66hajq "C. Line shape analysis">>

    时间序列包括两个不同的阶段：初始脉冲和长衰减尾迹。 直接透射. 间接透射，入射能量的剩余部分激发了导模共振。然后，共振中的功率从结构中缓慢衰减出来，产生长衰减尾。

    通过傅立叶变换，透射和反射光谱与时变场相关联。因此，研究电场的时间相关性是非常有用的。例如，我们在图 8~a 中显示了透射监测点的电场振幅与时间步长的函数关系，该计算得出了图 7 所示的光谱。时间序列包括两个不同的阶段：初始脉冲和长衰减尾迹。

    这两个阶段的存在表明在透射过程中存在两种途径。第一种途径是​直接透射过程，入射能量的一部分直接穿过板并产生初始脉冲。初始脉冲的傅里叶变换应能解释透射光谱中的背景。第二种途径是间接透射过程，入射能量的剩余部分激发了导模共振。然后，共振中的功率从结构中缓慢衰减出来，产生长衰减尾。通过对衰减尾迹进行傅立叶变换，我们可以得到典型的对称洛伦兹线形状，如图 8b 所示。

    透射监测点的电场振幅与时间步长的函数关系（注意从图6知，透射监视点在光子晶体板下方一段距离）

    ‍

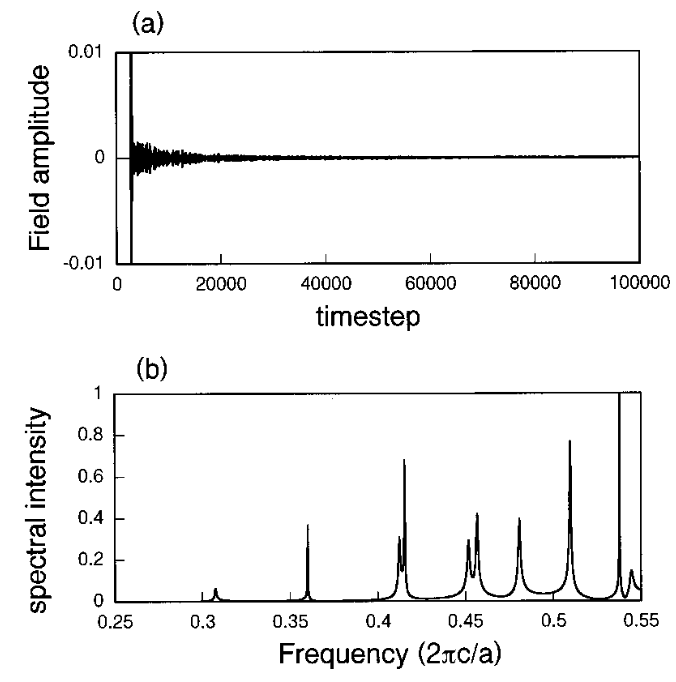    image请注意存在两个独立的阶段：初始脉冲和长的衰减尾流。b）时间步长为 20 000-100 000 的振幅的傅里叶变换。光谱强度呈现洛伦兹线型。

    对比图b和图7，可以看出，图b对应的就是在<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402120730-bpr01tb "parallel wave vector along the x direction k x=0.232p/a">>和s极化的光的入射情况下，导模共振的频率。

    MATLAB 数据处理（二）非线性拟合——洛伦兹拟合（Lorentz fit）-CSDN博客

    通过对<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402160412-th3dqhk " resonant line shape">>的分析，我们可以确定谐振的品质因数 Q。

    品质因数 Q 的定义是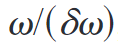image ，其中 \(\omega\) 是中心频率，\(d\omega\) 是谐振线宽。

    因此，整个透射谱图7，就是取决于直接和间接路径的干涉。【其实就是说有两种路径】

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402161602-jn1hp8y " The transmission property, therefore, is determined by the interference between the direct and the indirect pathways. The same observation can be made for the reflected amplitude as well. In solid-state and atomic physics, similar interference phenomena are commonly referred to as the Fano resonances.32 ">>

    后面的唯象数学模型解释了为什么是"干涉"！

    后面这部分作者介绍了一个有点唯象的数学模型 【毕竟这种现象太复杂了】

    ‍

    image，虽然有唯象参数，而且(9)(10)竟然是和均匀板的背景谱拟合得到的，但此理论与实验也一致

    ‍

    注意这部分数学理论开头就说了，是用来解释和考虑"干涉"的：<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240403102543-emddp38 "Taking into consideration the interference between these two pathways, we can construct a simple and intuitive model that quantitatively explains the line shape">>. 公式(3)中的f就是和间接透射过程有关：image，然而f最后算出来又是和直接透射过程有关：image，所以可以认为是"干涉"

    ‍

    D. Wave vector dependence of the resonances

    注意之前探索的情况是：<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402120730-bpr01tb " The incident wave is s polarized and has a">> <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402120730-bpr01tb "parallel wave vector along the x direction k x=0.232p/a">>

    ‍

    s极化和p极化

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402204206-8jufkgx "The s polarization has the electric field perpendicular to the plane of incidence, while the p polarization has the magnetic field perpendicular to the plane of incidence.">>

    入射面指的是：波矢 与 光子晶体板法线 构成的平面

    ‍

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402213308-qmap5ex "Incident waves with different polarizations excite different resonances, since the two polarizations possess different symmetries with respect to the yz-mirror plane">>

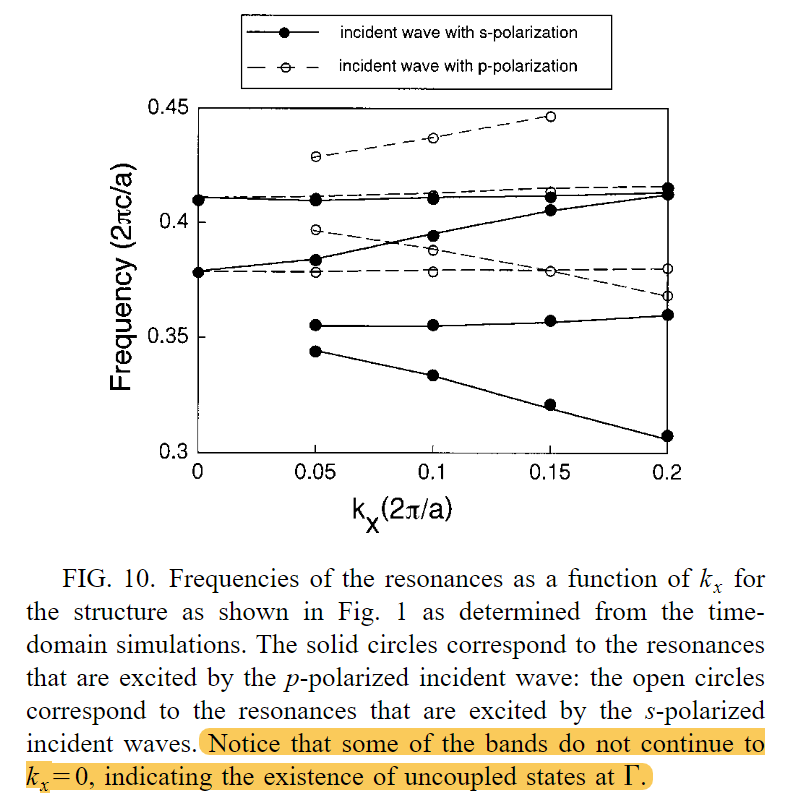
    首次提出Gamma点存在无耦合态（BIC）：Gamma 点的某些共振与入射波的任一偏振都不耦合，所有这些未耦合的共振都是单简并的

    我们注意到，在图 10 中，有些波段并没有延续到 Gamma 点。换句话说，Gamma 点的某些共振与入射波的任一偏振都不耦合。仔细观察图 10 可以发现，所有这些未耦合的共振都是单简并的。此前，Pacradoni 等人14 在实验中观察到了这种效应，Paddon 和 Young13 以及 Ochiai 和 Sakoda25 也对其进行了理论探讨。

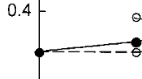    image

    注意image，在Gamma点有模式，说明这条实线是双简并的，也说明这条虚线也是双简并的。

    存在BIC时，透射谱：
    图10的含义：当kx=0，也就是说，对时域仿真得到的长衰减尾迹进行傅里叶变换，得到的透射谱，0.35这个频率的地方，不存在尖锐的线形，即Gamma 点的某些共振与入射波的任一偏振都不耦合。

    这就是BIC！

    在落日情的知乎回答中给出了kx=0（Gamma点），他画的透射谱image，这与论文图12中最后一个图是完全一样的：<<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240403104600-iijxq7q " we plot in Fig. 12 the transmission spectra at normal incidence ">>（正入射说明是\(\Gamma\)点）image。 图中我用红色圈出来的尖锐线形对应于图10中Gamma点的这两个黑色点： image 。若图10中最低的两个能带能够延续到Gamma点，则在Gamma点，0.35频率处应该还有尖锐的线形，但是现在没有尖锐的线形，说明Gamma 点的某些共振与入射波的任一偏振都不耦合！

    ‍

    Q因子与kx之间的关系：接近Gamma点时，单简并模式的Q因子发散 （说明BIC）

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402214039-pce2q6h " The Q factors">> <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402214055-u775w8r "approach a constant as k x vanishes for the modes that connect to the doubly degenerate states at G. ">>

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402214055-u775w8r "For the modes that connect to the singly degenerate states, on the other hand, the Q factors of the modes diverge.">>

    这说明模式对称性影响共振的光子寿命。

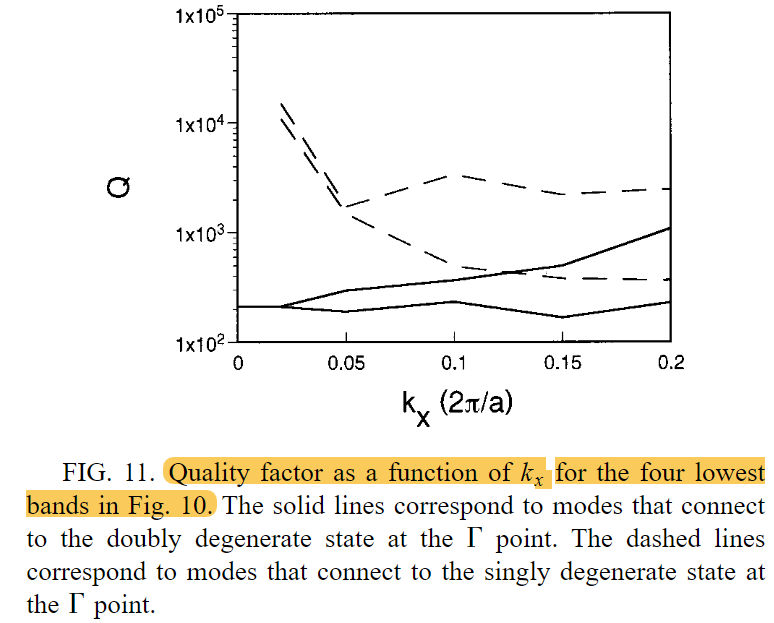
    image

    ‍

    E. Radius dependence of the resonance

    孔半径越小，Q因子越高

    除了与对称性相关的影响之外，共振的寿命还受到孔半径的强烈影响。在孔半径趋近于零的极限，所有共振的 Q 因子都会发散，因为共振渐近地成为真正的导模。

    为什么都变成真正的导模？

    为了证明这种效应，我们在图 12 中绘制了半径从 0.05a 到 0.20a 的四种不同结构在正常入射时的透射光谱。随着半径变小，共振的光谱特征确实变得更加尖锐。 对于最低阶的共振，Q 值从半径为 0.05a 时的约 5000 到半径为 0.20a 时的 213 不等。在更大的半径下，Q 因子应该更低。

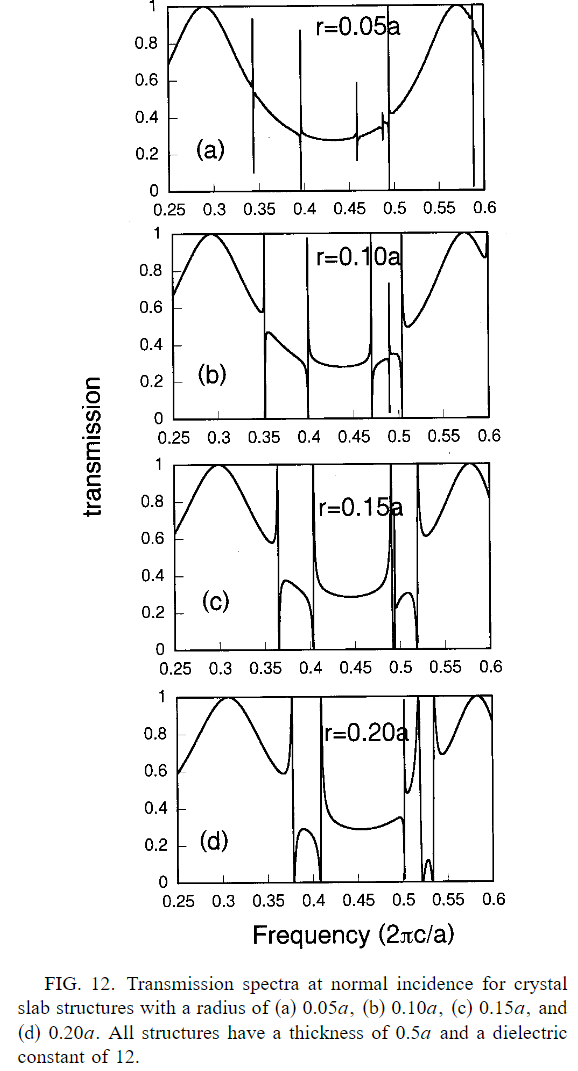
    image

    品质因数随孔半径的可调性对于发光二极管和激光应用非常重要。对于光子晶体谐振腔 LED 结构而言，当共振的线宽与发射器的线宽相当时，就能达到最佳效率35。因此，正如我们在本文中所展示的，光子晶体板结构用途非常广泛，可针对不同的发光应用进行专门定制。

    总结

    总之，我们对光子晶体板结构中的共振进行了三维频域和时域分析。这些共振与介质板紧密结合，同时又与辐射模式耦合。对于入射到这些板上的外部光，透射和反射光谱会因这些共振的存在而发生强烈变化。线形line shapes表现出复杂的不对称特征。我们的研究表明，线形的所有复杂性都可以用一个简单的分析模型来解释，该模型描述了直接透射（或反射）与共振的指数衰减振幅之间的干涉。我们还证明，这些共振的品质因数深受模式对称性和孔半径的影响。

    ‍ ↩︎ ↩︎

  2. 因此，整个透射谱图7，就是取决于直接和间接路径的干涉。【其实就是说有两种路径】

    <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402161602-jn1hp8y " The transmission property, therefore, is determined by the interference between the direct and the indirect pathways. The same observation can be made for the reflected amplitude as well. In solid-state and atomic physics, similar interference phenomena are commonly referred to as the Fano resonances.32 ">>

    后面的唯象数学模型解释了为什么是"干涉"！

    ↩︎

  3. 对称性保护的连续体束缚态（Symmetry-protected BIC）

    20世纪末人们就意识到，尽管布里渊区中心（Gamma point）处于Continuum之内（k∥=0 ），但有些模式却可以有无穷大的品质因子Q，即没有任何耗散[3]（即不会耗散到空气中）。这是因为这些模式的对称性与相匹配的平面波对称性不一致，从而导致二者之间的耦合为0。我们首先可以用模式的分布来简单地说明这一点：

    方晶格+简单圆洞构成的光子晶体平板中的TE1模式

    我们在上图展示了一个最简单的光子晶体平板（方形晶格中打一个贯穿的圆柱形洞）中在Gamma点的TE1模式。我们可以看到，其电场的x分量在原胞中是一个奇函数（上负下正），y分量也是一个奇函数（左负右正）。这个模式想和平面波耦合，但平面波的电场的x分量和y分量在原胞内均是恒定的常数（因为平面内波矢k∥为0，这是因为在Gamma点），也就是偶函数，于是这个模式和平面波的耦合自然为0（亦可以从上图中的积分给出，奇函数的积分自然是0）。

    每一个​本征模式​都是C4v的一个表示（representation）

    如果借助群论的语言，我们把上面的事实表达出来会十分容易：这里的系统具有旋转90度，沿x轴y轴镜像不变的对称性，于是系统可以用C4v这个群来描述，每一个​本征模式​都是C4v的一个表示（representation） 。我们把C4v的全部表示列在这里：

    C4v的特征标表

    从表里可以看出，我们这里考虑的C4v体系支持4种非简并的模式（A1，A2，B1，B2），1种简并的模式（E）。如果想判断一个模式属于哪个表示，就可以看上面的特征标表：如果模式的电磁场分布对于C4（90度旋转），C2（180度旋转），σv（沿x轴和y轴的镜面反射），σd（沿两条对角线的镜面反射）都是偶的，那么这个模式属于A1表示；如果仅对于两个镜面反射是奇的，那么就是A2，以此类推。而Gamma点的平面波属于E表示，这一点无论是从它的简并性质（容许x和y两种偏振态），还是直接读特征标表都可以看出。这也就意味着，C4v体系中的非简并模式和平面波都属于不同的表示，也就意味着至少在一种对称操作下二者奇偶性不同，进而可以看出全部的非简并模式均为Symmetry-protected BIC。而二维的简并模式E，由于和平面波同属一个表示，则不是Symmetry-protected BIC（但能不能通过别的机制成为BIC呢？见最后）。

    Symmetry-protected BIC的观测

    C4体系中对称保护的BIC首先被这两篇文章[4, 5]所观测到，基本上使得BIC的故事变得完整了。我们[4]为基础简单介绍Symmetry-protected BIC的观测：如果我们向光子晶体平板上照射一束激光，其频率 ω 和 平面内波矢 k∥=ksin⁡θ 均和光子晶体平板内的某个模式相匹配，这个模式就会被激发。 而我们收集到的反射光则由两部分构成 ：​一部分是光照到光子晶体平板后的直接反射（direct reflection），另一部分是被激发的光子晶体模式耗散掉的光子（被激发的光子晶体模式会向自由空间耗散光子） ，而这两部分的​相位差​是一定的（即相干的，就是02年Fan论文中说的"干涉"），所以反射谱会呈现非常独特的​Fano（法诺）线型 。 （这一部分的详细讨论请参见我关于耦合模理论的其他文章，这里不再赘述）通过拟合反射谱的Fano线型，我们就可以提取出这个被激发模式的品质因子Q，可以看到对于一维的模式，随着入射光的角度变小，即被激发的模式越来越接近布里渊区中心 Γ ，这一品质因子也增加，即看到了Symmetry-protected BIC。而对于二维的模式，我们看不到Q随入射角减小的增高。

    这部分对反射谱的说法，与02年Fan-2002-Analysis of guided resonances in photonic crystal slabs[1:1]是一致的，The transmission property, therefore, is determined by the interference between the direct and t...[5]中也说Fano线型。

    为什么"而对于二维的模式，我们看不到Q随入射角减小的增高。"？需要读文献4

    我们简单对这一实验做一总结：

    实验测得的光子晶体模式的Q还比较小，大约只有不到10000 （10的4次方）
    1. 首先我们可以看到光子晶体模式的Q还比较小，大约只有不到10000，这可能是因为在制造光子晶体时，不可避免会产生许多缺陷(defect) ，比如某些圆洞的直径会偏大或者偏小，圆心有所偏离等等。这些缺陷会将希望制备的光子晶体模式 (ω,k∥) 散射到其他的模式 (ω′,k∥′) ，而这些模式有些会比我们想要的BIC模式Q要低，能量进而通过这些模式耗散出去。之后我们可以看到，通过merging BIC的方法可以继续降低这一部分散射耗散，提升光子晶体模式的Q。
    在之后的很多实验中 ，科研人员都选择了​通过cross polarization的方法去掉了直接反射
    1. 第二点是这一实验由于收集了直接反射的这部分光，使得最后得到的反射谱是Fano线型，而对Fano线型的拟合相比Lorentz线型的拟合会比较困难，但可以通过耦合模理论给出内部品质因子Qi（如材料的吸收导致的损耗）和​Qe（通过辐射耗散导致的） 分别是多少，可以说是各有利弊。在之后的很多实验中 ，科研人员都选择了​通过cross polarization的方法去掉了直接反射 （直接反射的偏振一般与​入射偏振​一致，无论入射的偏振方向。但模式辐射的偏振一般不由入射偏振直接决定，而是由激发的模式决定，于是可以选择一个比较恰当的入射偏振，然后设置一个与之垂直的​偏振片​过滤掉直接反射，留下（一部分）的辐射）。
    临界耦合 临界耦合(也是Q因子为什么要定量可调)的物理应用和意义【在激光器、吸收器、传感器中都有应用】

    1. 这个实验结合仿真还揭示了这样一点：在布里渊区中心BIC处，Q是比较高的，尤其是外部品质因子Qe，应该此时会远远大于Qi。​而随着离开布里渊区中心的距离增加，Qe会逐渐降低，这中间可以达到Qe = Qi的一个匹配（我们通常称为critical couple，​临界耦合​），这在一些应用中是比较重要的。

    2. GPT：临界耦合的物理应用和意义【在激光器、吸收器、传感器中都有应用】

      为了实现模式竞争，实现单模，就应该这个模式的Q因子高。 然而Q因子越高，从"激光器的外部量子效率正比于 image Qioss tQradiation 其中 𝑄 l o s s ...[6]

      我们可以通过以下方式理解这一现象：不同的Q因子意味着边缘态具有不同的约束能力与不同的辐射损耗。因此，对于相同结构（相同本征损耗或耗散损耗），不同的辐射损耗会以不同方式耦合相同的本征损耗，从而产...[7]

      下面我用通俗易懂但严谨的方式把**临界耦合（critical coupling）**在 BIC / quasi-BIC 体系里的含义、数学表达、如何实现、能带来哪些有用效果（在传感、激光、非线性增强、吸收器与开关中的作用）以及常见的折中与注意事项都讲清楚。尽量少用专业晦涩的语句，必要时给出简单公式说明直观物理量的关系。

      一、先把概念说清楚 —— 什么是“临界耦合”？

      把一个被激发的光学谐振器想像成一个「水缸」：

      • 水缸有​内耗​（内部漏水或蒸发），我们称之为​内部损耗，在光学上对应于由材料吸收、散射等引起的损耗（用 \(Q_i\) 或损耗速率 \(\kappa_i\) 描述）。
      • 水缸还和外界有“开口”相连，可以通过那个口把水送进或放出，这对应光学上的​对外耦合/辐射损耗（用 \(Q_e\) 或耦合速率 \(\kappa_e\) 描述）。

      在频域下，一个谐振模的总损耗速率是两者之和：

      \[\kappa = \kappa_i + \kappa_e, \]

      对应的总品质因子是

      \[\frac{1}{Q}=\frac{1}{Q_i}+\frac{1}{Q_e}. \]

      临界耦合就是当对外耦合损耗等于内部损耗时的特别点：

      \[\kappa_e = \kappa_i \quad\text{或等价地}\quad Q_e = Q_i. \]

      物理含义（直观）：

      • 在临界耦合点，外界把能量耦入谐振器的速率恰好等于谐振器内部把能量耗掉（或散失）的速率。
      • 结果是在谐振频率上，外界与腔之间的能量“阻抗匹配”（impedance matching）最完美：入射能量被最大化地送入并在腔内被消耗或耦出（取决场景），在某些配置下会出现零反射 / 完全吸收或​最强的腔内场增强。

      更具体一点（常见单通道例子）：
      对单端口系统（例如入射光从同一直路进出），在谐振频率处，透射/反射强度 \(T\) 或 \(R\) 的表达式可以写成（简化形式，忽略相位）：

      \[T(\omega_0) \propto \left(\frac{\kappa_i-\kappa_e}{\kappa_i+\kappa_e}\right)^2. \]

      可以看到当 \(\kappa_i=\kappa_e\) 时，\(T(\omega_0)=0\) —— 也就是说反射或透射消失，能量被完全吸收或进入腔内（取决系统如何收集或损耗能量）。

      二、在 BIC / quasi-BIC 体系里为什么临界耦合特别重要？

      BIC（bound state in the continuum）的特点：

      • 理想 BIC 是完全不辐射的：​辐射损耗为零，即 \(Q_e\to\infty\)（或 \(\kappa_e\to0\)）。因此理想 BIC 本质上不能和外界耦合，难以被激发或提取能量——对很多实用器件并不直接有用。
      • 把 BIC「打破对称」或做轻微扰动，就得到 ​quasi-BIC​，它具有可调大的辐射 Q（即 \(Q_e\) 可在很宽范围内被调节），从无限变成一个很大的但有限的数。也就是说，quasi-BIC 平台允许我们在极宽范围内调节外辐射损耗 \(\kappa_e\) 。

      这就带来一个极大的好处：你可以把 ​\(Q_e\)​（外耦合）调到和材料吸收或其它内部损耗 ​\(Q_i\)​ 相等 —— 也就是到达​临界耦合。BIC 平台之所以方便，是因为 ​\(\,Q_e\)​ 可以被精细控制（通过几何的微小调整、破对称度、倾斜角度、邻近散射体等），所以容易实现 \(Q_e\approx Q_i\)。

      三、临界耦合能做什么？（按应用领域通俗说明）

      下面逐项说明临界耦合在常见光学应用中的具体用处和直观原因。

      1) 完美吸收器 / 光学探测器

      • 在单端口、无散射通路的情形下，临界耦合时入射光在谐振频率可被​完全吸收（反射/透射接近零）。
      • 这就是所谓的​critical-coupling perfect absorber，用于做光吸收探测器、热光探测器或太阳能薄膜等场景可以极大提高吸收效率。
      • 在 quasi-BIC 平台上，利用高腔场增强 + 临界耦合，可以在窄带上实现极高的吸收率（有利于窄带传感或光电探测）。

      2) 传感器（折射率 / 生物传感）

      • 传感器常常依赖腔谐振的峰位移动或峰值强度变化来检测周围环境的微小变化。临界耦合的优势有两点：

        1. ​大场增强：腔内场强最大，能增强与被测物（分子、层）的相互作用，放大响应信号。
        2. ​大对比度/极深谐振凹陷：在临界耦合时反射/透射在共振处极低，微小的折射率变化能造成强烈的光谱信号变化（便于检测）。

      • 注意一个折中：灵敏度的一项关键指标是 FOM（figure-of-merit）≈灵敏度／线宽。将 \(\kappa_e\) 调到等于 \(\kappa_i\) 会把总 Q 降到 \(Q_\text{tot}=Q_i/2\)（因为两者相等），导致线宽变宽一倍。也就是说：

        • 临界耦合提高信号对比与吸收，但可能牺牲一点分辨率（线宽变大）。
        • 对实际传感器设计来说，需要在“​信号对比​（contrast）”与“​解析度/线宽”之间权衡，视具体检测方式决定是否追求临界耦合。

      3) 激光器（尤其是 BIC / quasi-BIC 激光）

      • 对激光器而言有两个关键量：阈值（threshold） 与 ​输出耦出效率 / 斜率效率。总损耗越小阈值越低，但若外耦合太弱（\(Q_e\) 太大），虽然阈值低但能量难以输出（输出功率小）；若外耦合太强（\(Q_e\) 太小），阈值会变高（因为损耗增大）但输出耦出效率高。
      • 对某给定增益介质而言，存在一个​最佳耦合​（有时称为“阻抗匹配”或“匹配耦合”），在该点上​单位泵浦所能得到的输出功率最大。这个最佳点通常在 \(\kappa_e\) 与 \(\kappa_i\) 同阶甚至相当时出现——也就是接近临界耦合的区域。
      • 因此，quasi-BIC 能精细调节 \(\kappa_e\)，有利于把腔设计到最优输出点，既能保持较低阈值又能得到高耦出效率（较高的输出功率）。这是 BIC-based 激光器受关注的一个重要原因。

      4) 非线性效应与光学开关 / 调制器

      • 高场增强（腔内能量积累）能显著增加非线性效应（二次/三次谐波、四波混频、饱和吸收等）。在临界耦合/准临界条件下，腔内能量最大，非线性转换效率提高。
      • 在开关或调制器中，临界耦合可以带来高的灭/通比（extinction ratio）：通过微小的微结构调节改变 \(\kappa_e\) 或 \(\kappa_i\)，可以把传输从接近 0 切换到较高值，适合高对比度调制。

      5) 光学滤波 / 谐振增强光学器件

      • 临界耦合可以提供极深且可控的谐振凹陷（或峰），用于精密滤波或频率选择性吸收。

      四、如何实现/调节临界耦合（在 BIC 体系中尤其实用）

      1. 调整外辐射损耗（​\(\kappa_e\) 或 \(Q_e\)​ ）

        • 在 quasi-BIC：通过改变几何破对称度（如微小位移、孔径变化、侧向偏移角、倾斜入射等）可以把 \(Q_e\) 从非常高调小到较低值，范围可覆盖几个数量级，便于匹配 \(Q_i\)。
        • 在波导—谐振器耦合（ring/wg）场景：通过改变耦合间隙或耦合长度调整耦合率。

      2. 改变内部损耗（​\(\kappa_i\) 或 \(Q_i\)​ ）

        • 内损耗受材料吸收、散射、表面粗糙等影响，可通过材料选择（低吸收材料提高 \(Q_i\)）、引入吸收层（增加 \(\kappa_i\)）或通过温度/污染控制来调节。
        • 在某些设计中，人为引入薄膜吸收层使内部损耗与可控外泄损耗匹配，从而达到临界耦合。

      3. 反馈监测与精细调节

        • 实验上通常测反射/透射谱并实时调节结构参数（或温度、电场、载流子注入）直到在目标波长看到最大吸收或最深的反射凹陷——那就是临界耦合点。

      五、常见的数学判据（便于实验判断）

      对于单谐振、单入射通道的线性系统，有时采用耦合模式理论（coupled-mode theory）写出频域传输，谐振处（频率偏差 \(\Delta=0\)）的转输/反射为：

      \[T(0)=\left(\frac{\kappa_i-\kappa_e}{\kappa_i+\kappa_e}\right)^2. \]

      因此：

      • 若 \(\kappa_e=\kappa_i\) 则 \(T(0)=0\)：临界耦合（最大吸收/零反射）。
      • 若 \(\kappa_e\gg\kappa_i\)：过耦合，能量大部分辐射出去（反射/透射接近 1）。
      • 若 \(\kappa_e\ll\kappa_i\)：欠耦合，能量难以进入腔，腔内场弱。

      总 Q 的关系再重述一次：

      \[\frac{1}{Q_\text{tot}}=\frac{1}{Q_i}+\frac{1}{Q_e}. \]

      在临界耦合 \(Q_e=Q_i\) 时，\(Q_\text{tot}=Q_i/2\)。

      六、实际设计与折中（要注意的点）

      • ​临界耦合并不是万能的“提高灵敏度”开关：它最大化了腔内能量与吸收/耦出率，但同时会加宽线宽（总 Q 降低），所以对某些需要极窄线宽（超高分辨率频率位移传感）的应用，可能要取舍——有时保持更高的 \(Q_\text{tot}\)（欠耦合）能获得更好的频率分辨力。
      • ​对激光器而言，“最低阈值”与“最大输出”有竞争：极小的总损耗 → 低阈值但小输出（因输出耦合弱）；临界耦合提供了阈值与输出之间的折中，使输出效率最大化（所谓的阻抗匹配）。
      • ​对制造容差，quasi-BIC 的优势是 \(Q_e\) 可以被大范围调节，便于在实际制造的 \(Q_i\) 下找回匹配；但若材料吸收不稳定或散射太强，会使 \(Q_i\) 不稳定，从而临界点难以维持，需动态调节（热调、载流子注入等）。

      七、举例（直观联想，不列具体论文题名）

      • 在基于 quasi-BIC 的吸收器中，通过微小破对称得到 \(Q_e\) 与材料吸收损耗 \(Q_i\) 相等，实现窄带“完美吸收”——可用于窄带光探测或红外吸收器。
      • 在生物/气体传感中，临界耦合能使微小折射率变化在反射/透射上产生很大的对比度，便于用简单的强度测量（而非复杂的频移测量）完成检测。
      • 在 BIC-based 激光中，设计者通过调节破对称度把输出耦合调到合适的 \(\kappa_e\)，既保证低阈值又获得较高光输出。
      • 在非线性器件（如谐波产生）中，临界或接近临界的耦合可以使腔内场最大化，从而提升非线性转换效率。

      八、总结（一句话版）

      临界耦合就是把外耦合损耗和内部损耗“调成相等”，达到能量传输的“阻抗匹配”——在该点上腔内能量、吸收或输出最强。quasi-BIC 平台特别适合实现和利用临界耦合，因为它允许对外辐射损耗 \(Q_e\) 在极宽范围内精细调节，从而在传感、吸收器、激光与非线性器件中实现或优化很多有用的性能（如最大吸收、高场增强、最佳输出效率或高对比度调制），但实际应用中需要在对比度、线宽与阈值/输出之间做权衡。

      如果你需要，我可以：

      • 给出一两个具体的数学推导（例如透射系数如何从耦合模式理论得到）并画出示意性频谱（低耦合/临界/过耦合三种情况下的透射曲线）；或
      • 根据你手头的 BIC 结构（几何参数
    ↩︎

  4. 零级衍射范围，在物理光学书172页中，圆孔的夫琅和费衍射，中间是一个圆，光能量大部分集中在中央亮斑，艾里斑。 （注意从图5.37可以看出，是在动量空间） ↩︎

  5. <<assets/Fan-2002-Analysis of guided resonances in phot-20240401155006-vkck83n.pdf/20240402161602-jn1hp8y " The transmission property, therefore, is determined by the interference between the direct and the indirect pathways. The same observation can be made for the reflected amplitude as well. In solid-state and atomic physics, similar interference phenomena are commonly referred to as the Fano resonances.32 ">> ↩︎

  6. 为了实现模式竞争，实现单模，就应该这个模式的Q因子高。 然而Q因子越高，从"激光器的外部量子效率正比于 image其中 𝑄 l o s s 和 𝑄 r a d i a t i o n 分别是损耗通道和激光辐射通道的质量因子。"知，辐射通道的Q因子若越高，则辐射效率会越低。所以这里存在一个平衡，称为"临界耦合"。 这一点实现说可以查文献43、44，或直接谷歌搜 “辐射通道、临界耦合"
    • 临界耦合 临界耦合(也是Q因子为什么要定量可调)的物理应用和意义【在激光器、吸收器、传感器中都有应用】[8]

    ‍

    ‍ ↩︎ ↩︎

  7. 我们可以通过以下方式理解这一现象：不同的Q因子意味着边缘态具有不同的约束能力与不同的****辐射损耗 。 因此，对于相同结构（相同本征损耗或耗散损耗），不同的辐射损耗会以不同方式耦合相同的本征损耗，从而产生不同的透射峰（众所周知，当辐射损耗与本征损耗匹配时会产生临界耦合和完美吸收，导致零透射，因此在这种情况下，辐射损耗与本征损耗的不同耦合会导致不同的透射峰）。这表明损耗可能为基于eTBIC的传感提供一个额外的自由度。我们的传感方法不仅依赖于频率差异（透射峰频率Δω）来检测几何扰动，还考虑了振幅差异（透射峰高度）来检测与非厄米参数（如损耗和增益）相关的扰动。在此，我们提出利用峰值差异确定灵敏度最直接的方法之一，即通过两个峰之间的高度差来表征灵敏度。如图S20(b)所示，给出了基于峰高差别的灵敏度模拟结果。与图S20(a)通过频率分裂（即频率差）获得的灵敏度结果相比，基于峰值的灵敏度响应展现出有效区分全局扰动与横向扰动的能力。 ↩︎ ↩︎

  8. 临界耦合 临界耦合(也是Q因子为什么要定量可调)的物理应用和意义【在激光器、吸收器、传感器中都有应用】

    1. 这个实验结合仿真还揭示了这样一点：在布里渊区中心BIC处，Q是比较高的，尤其是外部品质因子Qe，应该此时会远远大于Qi。​而随着离开布里渊区中心的距离增加，Qe会逐渐降低，这中间可以达到Qe = Qi的一个匹配（我们通常称为critical couple，​临界耦合​），这在一些应用中是比较重要的。

    2. GPT：临界耦合的物理应用和意义【在激光器、吸收器、传感器中都有应用】

      为了实现模式竞争，实现单模，就应该这个模式的Q因子高。 然而Q因子越高，从"激光器的外部量子效率正比于 image Qioss tQradiation 其中 𝑄 l o s s ...[6:1]

      我们可以通过以下方式理解这一现象：不同的Q因子意味着边缘态具有不同的约束能力与不同的辐射损耗。因此，对于相同结构（相同本征损耗或耗散损耗），不同的辐射损耗会以不同方式耦合相同的本征损耗，从而产...[7:1]

      下面我用通俗易懂但严谨的方式把**临界耦合（critical coupling）**在 BIC / quasi-BIC 体系里的含义、数学表达、如何实现、能带来哪些有用效果（在传感、激光、非线性增强、吸收器与开关中的作用）以及常见的折中与注意事项都讲清楚。尽量少用专业晦涩的语句，必要时给出简单公式说明直观物理量的关系。

      一、先把概念说清楚 —— 什么是“临界耦合”？

      把一个被激发的光学谐振器想像成一个「水缸」：

      • 水缸有​内耗​（内部漏水或蒸发），我们称之为​内部损耗，在光学上对应于由材料吸收、散射等引起的损耗（用 \(Q_i\) 或损耗速率 \(\kappa_i\) 描述）。
      • 水缸还和外界有“开口”相连，可以通过那个口把水送进或放出，这对应光学上的​对外耦合/辐射损耗（用 \(Q_e\) 或耦合速率 \(\kappa_e\) 描述）。

      在频域下，一个谐振模的总损耗速率是两者之和：

      \[\kappa = \kappa_i + \kappa_e, \]

      对应的总品质因子是

      \[\frac{1}{Q}=\frac{1}{Q_i}+\frac{1}{Q_e}. \]

      临界耦合就是当对外耦合损耗等于内部损耗时的特别点：

      \[\kappa_e = \kappa_i \quad\text{或等价地}\quad Q_e = Q_i. \]

      物理含义（直观）：

      • 在临界耦合点，外界把能量耦入谐振器的速率恰好等于谐振器内部把能量耗掉（或散失）的速率。
      • 结果是在谐振频率上，外界与腔之间的能量“阻抗匹配”（impedance matching）最完美：入射能量被最大化地送入并在腔内被消耗或耦出（取决场景），在某些配置下会出现零反射 / 完全吸收或​最强的腔内场增强。

      更具体一点（常见单通道例子）：
      对单端口系统（例如入射光从同一直路进出），在谐振频率处，透射/反射强度 \(T\) 或 \(R\) 的表达式可以写成（简化形式，忽略相位）：

      \[T(\omega_0) \propto \left(\frac{\kappa_i-\kappa_e}{\kappa_i+\kappa_e}\right)^2. \]

      可以看到当 \(\kappa_i=\kappa_e\) 时，\(T(\omega_0)=0\) —— 也就是说反射或透射消失，能量被完全吸收或进入腔内（取决系统如何收集或损耗能量）。

      二、在 BIC / quasi-BIC 体系里为什么临界耦合特别重要？

      BIC（bound state in the continuum）的特点：

      • 理想 BIC 是完全不辐射的：​辐射损耗为零，即 \(Q_e\to\infty\)（或 \(\kappa_e\to0\)）。因此理想 BIC 本质上不能和外界耦合，难以被激发或提取能量——对很多实用器件并不直接有用。
      • 把 BIC「打破对称」或做轻微扰动，就得到 ​quasi-BIC​，它具有可调大的辐射 Q（即 \(Q_e\) 可在很宽范围内被调节），从无限变成一个很大的但有限的数。也就是说，quasi-BIC 平台允许我们在极宽范围内调节外辐射损耗 \(\kappa_e\) 。

      这就带来一个极大的好处：你可以把 ​\(Q_e\)​（外耦合）调到和材料吸收或其它内部损耗 ​\(Q_i\)​ 相等 —— 也就是到达​临界耦合。BIC 平台之所以方便，是因为 ​\(\,Q_e\)​ 可以被精细控制（通过几何的微小调整、破对称度、倾斜角度、邻近散射体等），所以容易实现 \(Q_e\approx Q_i\)。

      三、临界耦合能做什么？（按应用领域通俗说明）

      下面逐项说明临界耦合在常见光学应用中的具体用处和直观原因。

      1) 完美吸收器 / 光学探测器

      • 在单端口、无散射通路的情形下，临界耦合时入射光在谐振频率可被​完全吸收（反射/透射接近零）。
      • 这就是所谓的​critical-coupling perfect absorber，用于做光吸收探测器、热光探测器或太阳能薄膜等场景可以极大提高吸收效率。
      • 在 quasi-BIC 平台上，利用高腔场增强 + 临界耦合，可以在窄带上实现极高的吸收率（有利于窄带传感或光电探测）。

      2) 传感器（折射率 / 生物传感）

      • 传感器常常依赖腔谐振的峰位移动或峰值强度变化来检测周围环境的微小变化。临界耦合的优势有两点：

        1. ​大场增强：腔内场强最大，能增强与被测物（分子、层）的相互作用，放大响应信号。
        2. ​大对比度/极深谐振凹陷：在临界耦合时反射/透射在共振处极低，微小的折射率变化能造成强烈的光谱信号变化（便于检测）。

      • 注意一个折中：灵敏度的一项关键指标是 FOM（figure-of-merit）≈灵敏度／线宽。将 \(\kappa_e\) 调到等于 \(\kappa_i\) 会把总 Q 降到 \(Q_\text{tot}=Q_i/2\)（因为两者相等），导致线宽变宽一倍。也就是说：

        • 临界耦合提高信号对比与吸收，但可能牺牲一点分辨率（线宽变大）。
        • 对实际传感器设计来说，需要在“​信号对比​（contrast）”与“​解析度/线宽”之间权衡，视具体检测方式决定是否追求临界耦合。

      3) 激光器（尤其是 BIC / quasi-BIC 激光）

      • 对激光器而言有两个关键量：阈值（threshold） 与 ​输出耦出效率 / 斜率效率。总损耗越小阈值越低，但若外耦合太弱（\(Q_e\) 太大），虽然阈值低但能量难以输出（输出功率小）；若外耦合太强（\(Q_e\) 太小），阈值会变高（因为损耗增大）但输出耦出效率高。
      • 对某给定增益介质而言，存在一个​最佳耦合​（有时称为“阻抗匹配”或“匹配耦合”），在该点上​单位泵浦所能得到的输出功率最大。这个最佳点通常在 \(\kappa_e\) 与 \(\kappa_i\) 同阶甚至相当时出现——也就是接近临界耦合的区域。
      • 因此，quasi-BIC 能精细调节 \(\kappa_e\)，有利于把腔设计到最优输出点，既能保持较低阈值又能得到高耦出效率（较高的输出功率）。这是 BIC-based 激光器受关注的一个重要原因。

      4) 非线性效应与光学开关 / 调制器

      • 高场增强（腔内能量积累）能显著增加非线性效应（二次/三次谐波、四波混频、饱和吸收等）。在临界耦合/准临界条件下，腔内能量最大，非线性转换效率提高。
      • 在开关或调制器中，临界耦合可以带来高的灭/通比（extinction ratio）：通过微小的微结构调节改变 \(\kappa_e\) 或 \(\kappa_i\)，可以把传输从接近 0 切换到较高值，适合高对比度调制。

      5) 光学滤波 / 谐振增强光学器件

      • 临界耦合可以提供极深且可控的谐振凹陷（或峰），用于精密滤波或频率选择性吸收。

      四、如何实现/调节临界耦合（在 BIC 体系中尤其实用）

      1. 调整外辐射损耗（​\(\kappa_e\) 或 \(Q_e\)​ ）

        • 在 quasi-BIC：通过改变几何破对称度（如微小位移、孔径变化、侧向偏移角、倾斜入射等）可以把 \(Q_e\) 从非常高调小到较低值，范围可覆盖几个数量级，便于匹配 \(Q_i\)。
        • 在波导—谐振器耦合（ring/wg）场景：通过改变耦合间隙或耦合长度调整耦合率。

      2. 改变内部损耗（​\(\kappa_i\) 或 \(Q_i\)​ ）

        • 内损耗受材料吸收、散射、表面粗糙等影响，可通过材料选择（低吸收材料提高 \(Q_i\)）、引入吸收层（增加 \(\kappa_i\)）或通过温度/污染控制来调节。
        • 在某些设计中，人为引入薄膜吸收层使内部损耗与可控外泄损耗匹配，从而达到临界耦合。

      3. 反馈监测与精细调节

        • 实验上通常测反射/透射谱并实时调节结构参数（或温度、电场、载流子注入）直到在目标波长看到最大吸收或最深的反射凹陷——那就是临界耦合点。

      五、常见的数学判据（便于实验判断）

      对于单谐振、单入射通道的线性系统，有时采用耦合模式理论（coupled-mode theory）写出频域传输，谐振处（频率偏差 \(\Delta=0\)）的转输/反射为：

      \[T(0)=\left(\frac{\kappa_i-\kappa_e}{\kappa_i+\kappa_e}\right)^2. \]

      因此：

      • 若 \(\kappa_e=\kappa_i\) 则 \(T(0)=0\)：临界耦合（最大吸收/零反射）。
      • 若 \(\kappa_e\gg\kappa_i\)：过耦合，能量大部分辐射出去（反射/透射接近 1）。
      • 若 \(\kappa_e\ll\kappa_i\)：欠耦合，能量难以进入腔，腔内场弱。

      总 Q 的关系再重述一次：

      \[\frac{1}{Q_\text{tot}}=\frac{1}{Q_i}+\frac{1}{Q_e}. \]

      在临界耦合 \(Q_e=Q_i\) 时，\(Q_\text{tot}=Q_i/2\)。

      六、实际设计与折中（要注意的点）

      • ​临界耦合并不是万能的“提高灵敏度”开关：它最大化了腔内能量与吸收/耦出率，但同时会加宽线宽（总 Q 降低），所以对某些需要极窄线宽（超高分辨率频率位移传感）的应用，可能要取舍——有时保持更高的 \(Q_\text{tot}\)（欠耦合）能获得更好的频率分辨力。
      • ​对激光器而言，“最低阈值”与“最大输出”有竞争：极小的总损耗 → 低阈值但小输出（因输出耦合弱）；临界耦合提供了阈值与输出之间的折中，使输出效率最大化（所谓的阻抗匹配）。
      • ​对制造容差，quasi-BIC 的优势是 \(Q_e\) 可以被大范围调节，便于在实际制造的 \(Q_i\) 下找回匹配；但若材料吸收不稳定或散射太强，会使 \(Q_i\) 不稳定，从而临界点难以维持，需动态调节（热调、载流子注入等）。

      七、举例（直观联想，不列具体论文题名）

      • 在基于 quasi-BIC 的吸收器中，通过微小破对称得到 \(Q_e\) 与材料吸收损耗 \(Q_i\) 相等，实现窄带“完美吸收”——可用于窄带光探测或红外吸收器。
      • 在生物/气体传感中，临界耦合能使微小折射率变化在反射/透射上产生很大的对比度，便于用简单的强度测量（而非复杂的频移测量）完成检测。
      • 在 BIC-based 激光中，设计者通过调节破对称度把输出耦合调到合适的 \(\kappa_e\)，既保证低阈值又获得较高光输出。
      • 在非线性器件（如谐波产生）中，临界或接近临界的耦合可以使腔内场最大化，从而提升非线性转换效率。

      八、总结（一句话版）

      临界耦合就是把外耦合损耗和内部损耗“调成相等”，达到能量传输的“阻抗匹配”——在该点上腔内能量、吸收或输出最强。quasi-BIC 平台特别适合实现和利用临界耦合，因为它允许对外辐射损耗 \(Q_e\) 在极宽范围内精细调节，从而在传感、吸收器、激光与非线性器件中实现或优化很多有用的性能（如最大吸收、高场增强、最佳输出效率或高对比度调制），但实际应用中需要在对比度、线宽与阈值/输出之间做权衡。

      如果你需要，我可以：

      • 给出一两个具体的数学推导（例如透射系数如何从耦合模式理论得到）并画出示意性频谱（低耦合/临界/过耦合三种情况下的透射曲线）；或
      • 根据你手头的 BIC 结构（几何参数
    ↩︎
posted @ 2025-12-22 17:17  初心如磐使命在肩！  阅读(0)  评论(0)    收藏  举报