时间反演对称性

时间反演对称性资料

写得最好的：

不推荐读曾书量子力学卷二中关于时间反演对称性的内容，我感觉有错误。

时间反演对称性对无自旋情况时布洛赫波的影响

写得最好的是见wps云文档中Time_reversal_I_operator这个文档再加上sipe00论文中注释[25]来理解。

时间反演对称性对有自旋情况时布洛赫波的影响

写得最好的是见wps云文档中handout_symmetry这个文档，这个文档应该是参考了kittel的固体量子理论书，然后再作者原创的，我需要认真读这个文档，能读懂，写得好。
然后再学kittel的固体量子理论书.

kittel书的内容：

kittle.固体量子理论-重要-时间、空间反演对称性对含自旋的布洛赫波的影响

在稻壳阅读器中搜：c.kittel quantum theory of solids，第二版，181页开始：(dresshauls的一些论文关于自旋轨道耦合与时间反演引用的是这本书，比如她的一篇：石墨中的自旋轨道耦合；wps云文档中handout_symmetry中参考的也是这本书，因为作者的课中参考文献就是有kittel的这本书）

特别注意在存在SOC时，布洛赫波本征态，旋量的两个分量其实都有，见(26)

在(26)下面一段话中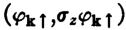，image.png是自旋的平均值！通过它是正还是负来区分态是自旋向上还是自旋向下！

b445c617628e740d130f51f47bbc6ad.pngimage.png

image.pngimage.png

image.png（这些题可能可以通过sakurai书的一些内容可以证明）

(35.2)的证明：

注意(35)是在存在SOC时也成立。

利用时间反演对称性的反幺正性质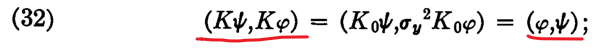image.png[在sakurai的现代量子力学书中也有证明]，故

\[\begin{equation} \begin{aligned} \left(\varphi_{\mathbf{k}\uparrow} , \sigma_{z} \varphi_{\mathbf{k} \uparrow}\right) &=\left(K \sigma_{z} \varphi_{\mathbf{k}\uparrow} , K{\varphi_{\mathbf{k}\uparrow} }\right) \\ &=\left(-i \sigma_{y} K_{0} \sigma_{z} \varphi_{k \uparrow},-i \sigma_{y} K_{0} \varphi_{k \uparrow}\right) \\ &=-\left(-i \sigma_{z} \sigma_{y} K_{0} \varphi_{k \uparrow},-i \sigma_{y} K_{0} \varphi_{k \uparrow}\right) \\ &=-\left(\sigma_{z} K \varphi_{k \uparrow}, K \varphi_{k \uparrow}\right) \\ &=-\left(\sigma_{z} \varphi_{-k ?}, \varphi_{-k ?}\right) \\ &=-\left(\varphi_{-k ?}, \sigma_{z} \varphi_{-k ?}\right) \end{aligned} \end{equation} \]

其中第三个等号的得出用了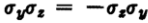image.png，第五个等号的得出用了(26)，但此时只知道\(K \varphi_{k \uparrow}\)得到的态与-k有关，还不知道自旋是怎么变化，所以写成\(K \varphi_{k \uparrow}=\varphi_{-k ?}\)。最后一个等号的得出是利用了将\(\sigma_z\)看成算符，可以知道它是厄米和幺正算符，有\(\sigma_z=\sigma_z^{\dag}\)，然后用量子力学笔记本中厄米共轭的性质，就得到最后一个等号。从上面这个公式可以看出，时间反演后的态的自旋与时间反演操作前的自旋相反，故(26)得证。

注：其实时间反演作用于带自旋的布洛赫态后自旋会相反这个结论在wps云文档中handout_symmetry这个pdf中证明更严谨。

dresshauls书16.3节是正确的，但16.4节是错误的

对于考虑自旋轨道耦合时布洛赫波在时间反演对称性下的性质，在kittel固体量子理论书中写的才是对的，dresshuals16.4节是错误的。

付亮06年的时间反演极化论文中时间反演操作对布洛赫波振幅的公式(3.10) 与 kittel的理论有区别吗?哪个对？以后再说

时间反演对称性对产生湮灭算符的作用

待续

空间反演对称性

写得最好的是见wps云文档中handout_symmetry这个文档，这个文档应该是参考了kittel的固体量子理论书，然后再作者原创的，我需要认真读这个文档，能读懂，写得好。
然后再学kittel的固体量子理论书.

posted @ 2022-06-02 22:19  初心如磐使命在肩！  阅读(448)  评论(3)    收藏  举报