PCR论文学习

论文《Progressive Correspondence Regenerator for Robust 3D Registration》

背景

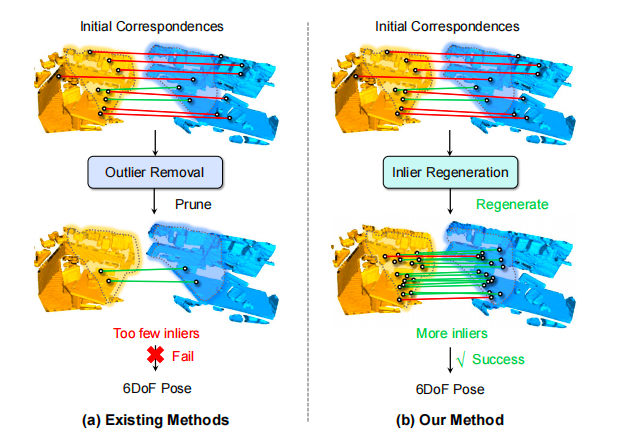
如图所示，以往的工作在进行离群值和内点区分的时候，对于离群值，直接进行修剪，只保留对应正确的内点，而本论文则不同，对于离群值，我们以它作为基础，进行新一轮的内点生成，并继续迭代，直至内点数满足要求。

具体工作

整体架构

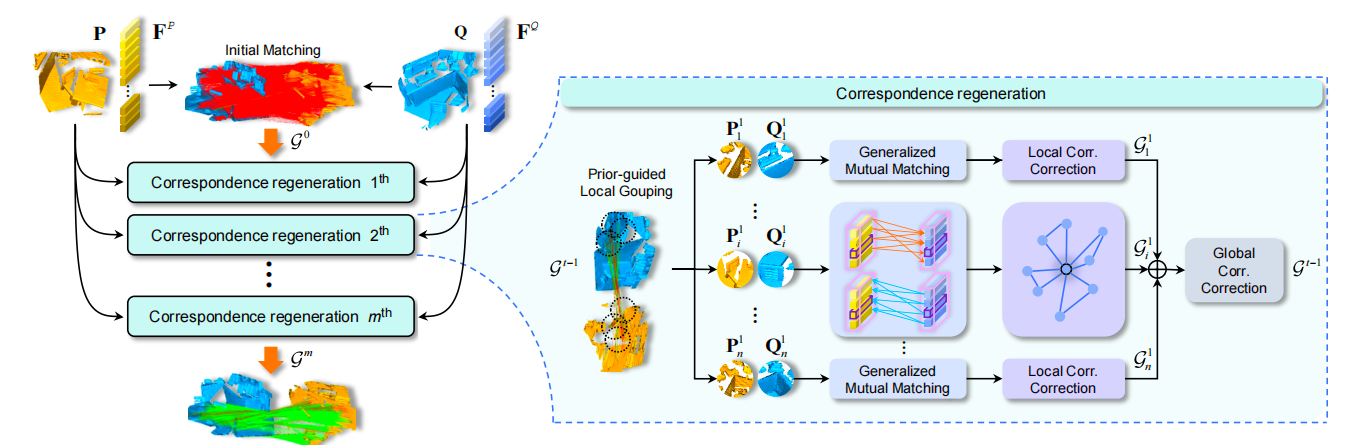
整体架构图如上，P是源点云，Q是目标点云，分别对P和Q提取特征后得到Fp、Fq，接下来我们进行初匹配，在第一次匹配之后，得到最初的对应关系g0，我们以g0为开始进行迭代，每次都以gt-1为输入，进行对应关系重建（Correspondence regeneration），在对应关系重建中，主要的操作是从gt-1的对应关系中，采用一部分作为种子对应，以种子为中心画圆得到局部区域，形成Pi和Qi，接着每一个局部区域都进行广义互匹配得到新的对应关系，然后使用三元组一致性对对于关系进行再次细化，最终进行合并操作得到全局的对应关系，通过SVD方法得到精确的旋转矩阵R和平移变量t

本地分组和重新匹配

首先我们来看上文中所说的，在进行初匹配之后，我们是通过种子进行画圆得到的各个局部区域，在这里是如何进行具体实现的。

我们以前一阶段的对应关系gt-1为输入，在这里使用了随机采样的方式进行采样，以此来得到种子，然后对每个种子，我们以当前种子为中心点，设立半径r，进行半径为r的最近邻搜索，以此获得局部点云Pi和Qi，每个都是如此，对应公式如下

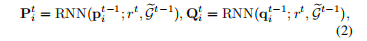
i的值从1遍历到n，这样我们就得到了n组的局部对应关系（Pi，Qi）。

接下来就是重新匹配模块，即广义互匹配模块。

传统的最近邻，也就是NN匹配会使得我们找到的对应关系过多，这中间会产生大量离群值，即错误匹配的对应点，但是如果采用互最近邻匹配，就会使得满足要求的对应关系很少，我们的广义互匹配模块则是取了一个中间态，它既使用了NN，也使用了MNN进行规范对应点，具体如下

在这里，我们给定点云Q作为查询，对其执行k最近邻搜索可获得最近邻匹配矩阵M1(p->q)和互最近邻矩阵M2(p->q)

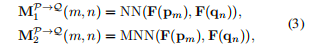
若满足条件则将值设为1，这是P->Q的，同理我们可以得到M1(q->p)和M2（q->p)，这个时候我们就有了四个矩阵。

接下来我们通过计算NN和MNN的哈达玛乘积，就可以得到相互匹配矩阵M*(p->q)和M*(q->p)，我们在这里进行或操作，以此来放宽条件，获得广义互匹配矩阵

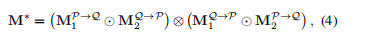
通过M*,我们获得了n组局部对应关系gi_t

局部对应关系优化

在重新匹配过后，由于部分原因，比如遮挡、初始对应关系不准确等，可能仍会引入部分错误对应关系。因此，我们进一步通过局部对应关系优化来提升对应关系的质量，这里使用的是中心感知三点一致性的方法，具体如下:

我们使用的是来自前一阶段的种子对应点gt-1，我们任选两个点对gi=(pi,qi)和gj=(pj,qj)，然后计算两者之间的一致性，如果两者都是正确的，那么pi和pj的距离，应该与qi和qj的距离是几乎一致的

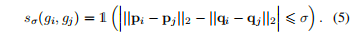
但有时可能存在情况是种子对应点并非是正确的，仅依靠此可能引发一系列的错误，比如pi和qi这个对应关系错误，那么即使pj和qj对应正确，计算这个距离时仍是不满足要求的，所以这里我们就需要进行再次优化，因此这里提出了双路径检测

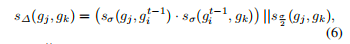
第一个是中心点传递一致性，如果gi和gi_t-1与gi_t-1和gk都满足，那么证明gi和gk是正确的对应点，第二个则是将阈值限制的更加严格，若满足则也能说明是正确的，两者存在一个正确的即可。

接下来我们定义了一个综合评分函数，我们设定阈值，计算S的L1范式，具体公式如下

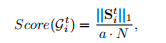
如果满足要求则视为正确的对应区域。

我们对每个点对都进行这样的操作，就可以找出全部的正确对应区域。

局部对应修正

在获取了全部的正确对应关系之后，我们挑选出得分最高的一部分，通过这部分计算出对应的局部变化矩阵R和平移向量t

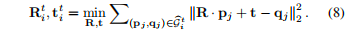
然后以此来修正所有点对，具体操作是，我们对p进行变换，然后在目前点云中寻找最近点q'，以此来得到新的q，公式如下

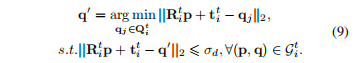
全局对应关系优化

在上个模块之后，我们得到了n组优化后的局部对应关系，但是不同关系之间可能存在重叠等情况，所以我们这里需要进行处理。

这里使用的合并方式是通过哈希表进行合并，举个例子

区域1：{(p1,q1), (p2,q2), (p3,q3)}
区域2：{(p2,q2), (p4,q4), (p5,q5)}  ← 重叠p2,q2
区域3：{(p3,q3), (p5,q5), (p6,q6)}  ← 重叠p3,q3, p5,q5

使用哈希表进行合并后为{(p1,q1), (p2,q2), (p3,q3), (p4,q4), (p5,q5), (p6,q6)}

合并之后，我们仍然需要进行一次优化，之前的都是局部一致性，这里我们是对全局进行一致性的检验，采用的方法是二阶一致性方法，前文中的中心感知一致性就是基于一阶一致性，它只考虑了距离，那么什么是二阶一致性呢，在考虑距离的基础上，加上了对角度的检验，也就是说，不仅要保持距离的一致，同时要保持角度的一致。然后寻找最大一致子集，估计出全局变换R和t，修正所有点对，以此来得到更好的对应关系。