《Buffer-X》论文学习

前置知识

PCA

PCA，即主成分分析，它通过正交变换将一组可能相关的变量转换为一组线性不相关的变量，这些新的变量称为主成分。具体计算方式如下：

首先需要对数据进行标准化处理，确保每个特征的均值为0，标准差为1

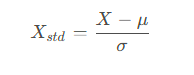
其中的X是原始数据矩阵，μ是每个特征的均值向量，σ是每个特征的标准差向量。

接下来就是计算协方差矩阵，协方差矩阵描述了数据集中各特征之间的相关性，其计算公式如下:

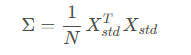
其中，N是数据点的数量。

然后是求解协方差矩阵的特征值和特征向量，通过特征向量，我们可以知道数据的变化方向，通过特征值，我们可以知道每个方向的深入程度，具体计算方式如下：

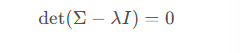
解出特征值λ后，再使用如下方式解出特征向量v

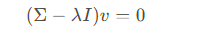
接下来就是选择主成分了，选择出最大的k个特征值对应的特征向量，通常这些特征向量对应的数据变化最大，将这些特征向量组合构造出投影矩阵

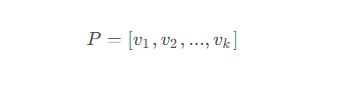
最后将原始数据通过这个投影矩阵变换到新的空间，就得到了降维的数据

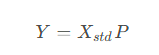
FPS

FPS，即最远点采样方法，它的思路可以简单理解如下：

1、选定一个点P，作为起始点
2、在给定范围内寻找距离P最远的点Pi，作为第二个点
3、重复第二步操作，直至点数满足要求

整体架构

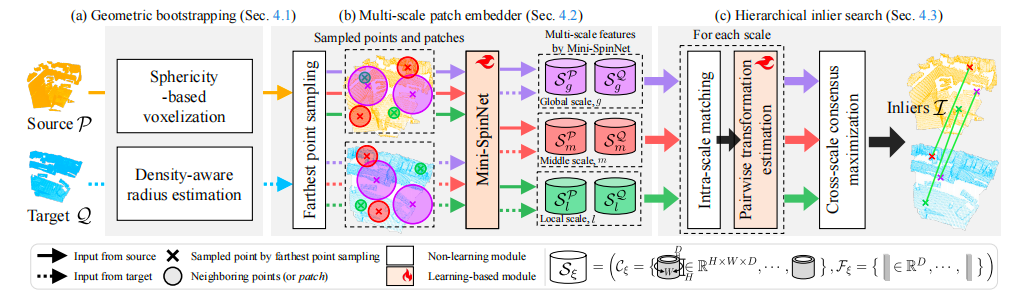
几何引导法

基于球形度的体素化

这里我们首先通过球形度来确定合适的体素大小v，体素就相当于二维图像中的像素块，这里我们定义一个函数h(P,Q)用于选出一个较大的点云（即从源点云和目标点云中选出较大的那个），这是因为点云个数多的通常包含更多空间信息，结果往往更可靠。这个时候我们去使用g(P，σ)去采样σ%的点，然后计算协方差矩阵，具体计算如下图

这里得到了C之后我们就可以去解特征值和特征向量了

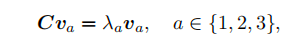
这里会得到三个特征值，我们将λ3/λ1作为球形度的计算方式，值越接近1就越接近球形，然后我们设定一个阈值，然后根据其球形度，分配不同大小的体素，计算方式如下图

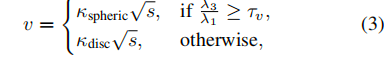
其中，

κ_spheric：用于球形点云的比例系数

κ_disc：用于扁平点云的比例系数

这里的Psampled=g(h(P,Q),σ)

密度感知半径估计

这里并没有和其他论文中选定固定范围作为半径，这里采用的是密度感知的方法，即通过考虑输入点密度来分别在局部、中间和全局尺度上确定r，具体计算方式如下：

我们这里定义Pq为查询点，围绕这个点查找邻居，首先定义邻域搜索函数

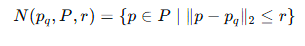
这个函数的含义是只找区域在r内的点作为点Pq的邻居

然后就是密度感知半径估计公式

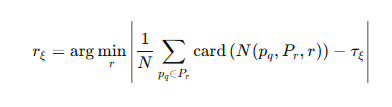
这里我们的r是一个变量，card表示邻居的数量，1/N则是为了进行平均，然后我们定义三个不同的τ作为阈值，不断调整r去逼近τ，作为最终的r，我们以此方式得到三个尺度的r。

之后我们进行尺度归一化将范围规定到[-1,1]，这样我们使得所有尺度的分块保持一致性。

多尺度嵌入模块

现在我们已经有了体素化点云和三个不同尺度的半径，接下来我们在每一尺度下生成基于补丁的描述符。

最远点采样

我们首先使用FPS在每个尺度中采样，FPS即最远点采样，这样可以保证覆盖的最全面，这里不同的是我们并未对同一采样点提取局部、中间和全局尺度的描述子，而是为每个尺度独立采样不同的点，即采样一部分点用于局部，另一部分用于中间尺度，还有一部分用于全局，这是因为经过实验发现不同区域可能需要不同的尺度才能实现最优特征提取。

基于Mini-SpinNet的描述符生成

我们使用多个半径在三个不同尺度采样补丁，从而获取更全面的多尺度表示。我们这里使用Mini-SpinNet进行描述符生成，这个是SpinNet的轻量级版本，但在此之前我们先进行了归一化，使得尺度保持一致性，接下来我们固定补丁大小，固定分块大小为Npatch，超过此大小时就进行随机采样，少的话重复采样，这样就保证了点数在不同尺度下保持一致。

在此之后我们将这些归一化的块作为输入，Mini-SpinNet会输出一个特征向量Fp和圆柱特征图Cp

跨尺度匹配

这里使用的是基于最近邻进行互匹配，在Fp和Fq之间，找到点都是相互匹配的，通过这种方法得到每个尺度下的匹配对应关系A，然后我们从中提取元素并采样关键点Pɛ和Qɛ。

配对转换估计

这里我们首先需要转换坐标系，因为目前的这个坐标系和世界坐标系是存在一个旋转关系的，具体的变换方式如下

即使两个补丁都对齐到自己的表面法线，它们绕法线方向的相对旋转（yaw）还是未知的。

这里的具体计算方式如下

将三部分组合就可以得到了R

然后有了R，t也就好得到了，代入就可以

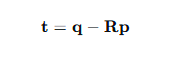
此时有很多个匹配对，我们找到跨尺度一致的可靠匹配，然后使用这些可靠的匹配对再放入RANSAC算法中进行估计变换，得到最终的R和t