深度学习基础从0到0.1
线性回归
一元线性回归
线性回归,公式为Y=Wx+b,这里简单一点,假设偏置b=0,我们设置损失函数为loss=(y-yi)²,y是真实值,yi是预测值,代入可得loss=(y-W*x)²,带入x的值和y的值即可得到最终的loss函数,而后求其导数,导数为0时可取极值,进而得到w,通过这样我们就可以得到最佳的拟合直线,而这就是线性回归算法,不过这里更为简单,还没对w进行训练。
那么如果考虑偏置b的话,我们又该怎么做呢,实际上很简单,我们只需要分别对两个变量求偏导,令其等于0即可,而后联立方程组解出变量值,示例如下
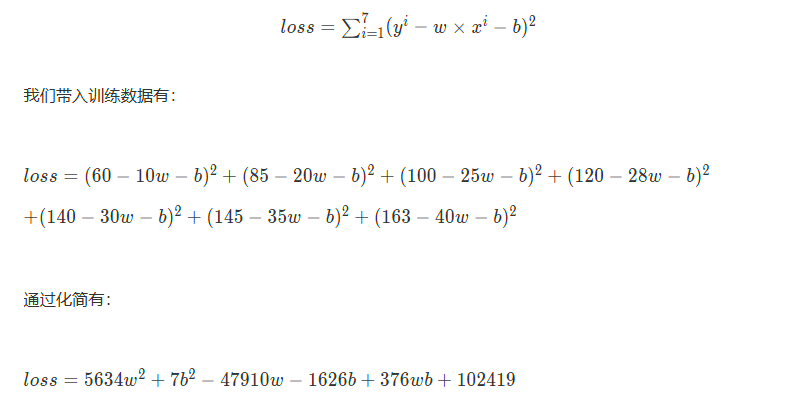
这里首先得出了loss函数,接下来对其进行求偏导
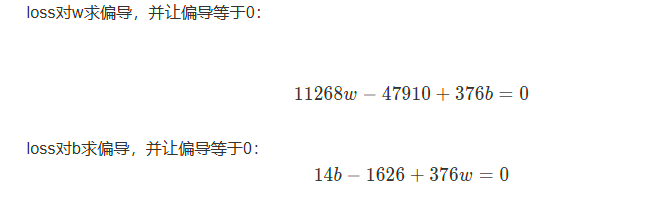
而后联立方程求解即可得出最终变量值。
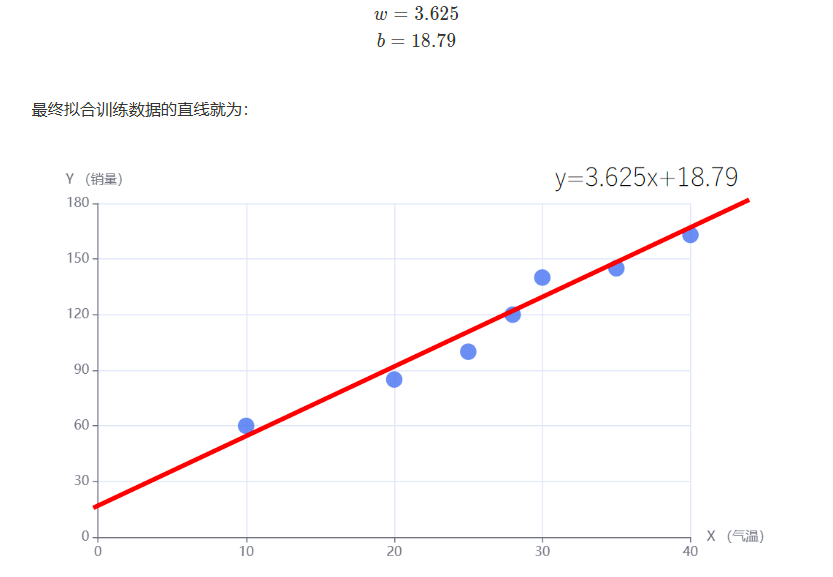
梯度下降
如果按照之前的思路,只要能够保证函数是线性的,我们无需再对模型进行多次微调,只需要令参数的偏导数全等于0求出函数即可,但为什么深度学习里不这么做呢,原因如下
1、参数可能有很多,成千上万,计算量过大
2、模型有可能不是线性的,引入了激活函数,比如Relu函数是分段的,对其求导,解方程将什么复杂
示例如下图,肉眼可见的方程是难以进行计算的

因此,我们这里就需要学习梯度下降,通过它来进行调参。
这里以一元函数为例,如下图所示,我们假设初始点为Xo=4,

接下来根据其导数进行调整,比如f'(x)>0,那说明函数是增大的,我们是想取f(x)的最小值,则我们需要向左调整,反之则向右调整;
那么我们如何设定这个调整的步长呢,这里有一个简单的方法,设置步长为负的f'(x),比如x=4的导数值f'(x)≈1,那我们就设置为-1,接下来x的值就会由4变为3,
可以发现离最小值更近了一步,在x=3处的f'(x)为0.7,接下来进行-0.7,变为2.3。这样不断逼近最终就抵达了最低点。
学习率
上面可以看出更新的步长貌似还不错,但是实际上还需要一个参数去调控步长,这个参数一把不大于1,比如0.01,因为有时候直接使用步长操作可能会错过全局最小值,所以我们引进学习率调控。这里就可以开始更新参数了,我们在求导后,加上了学习率,然后不断对参数进行更新迭代,直至达到最优版本。
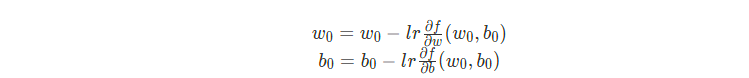
均方误差
之前我们定义的损失函数是所有样本的label和预测值的误差的平方和,实际上为了保证训练稳定,一般会除以样本数,而这其实就是我们的均方误差。

多元线性回归
刚刚所看的是一元线性回归,那么多元线性回归又当如何呢?实际上是一样的处理过程,具体示例如下
数据如下:
| 温度 | 价格(元) | 销量(个) |
|---|---|---|
| 10 | 3 | 60 |
| 20 | 3 | 85 |
| 25 | 3 | 100 |
| 28 | 2.5 | 120 |
| 30 | 2 | 140 |
| 35 | 2.5 | 145 |
| 40 | 2.5 | 163 |
这里用X1表示温度,X2表示价格,Y表示销量。
Wo表示截距(初始值),W1表示温度权重,W2表示价格权重。
预测销量为Y=Wo+X1*W1+X2*W2。
损失函数loss=1/7∑(y-yi)²,代入就是loss=1/7∑(Wo+X1*W1+X2*W2-yi)²
接下来就是用刚刚所学的梯度下降进行优化,而梯度下降首先就是求导数,所以我们分别对三个变量进行求偏导。
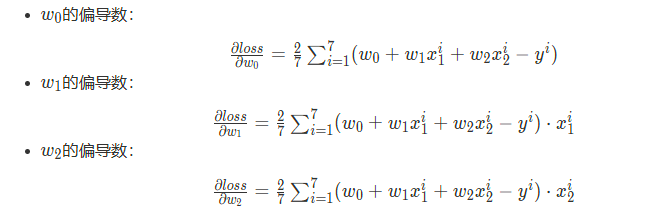
在这之后设置学习率,而后更新参数即可
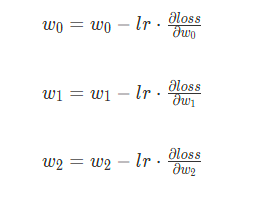
具体实现代码如下
# Feature 数据
X = [[10, 3], [20, 3], [25, 3], [28, 2.5], [30, 2], [35, 2.5], [40, 2.5]]
y = [60, 85, 100, 120, 140, 145, 163] # Label 数据
# 初始化参数
w = [0.0, 0.0, 0.0] # w0, w1, w2
lr = 0.0001 # 学习率
num_iterations = 10000 # 迭代次数
# 梯度下降
for i in range(num_iterations):
# 预测值
y_pred = [w[0] + w[1] * x[0] + w[2] * x[1] for x in X]
# 计算损失
loss = sum((y_pred[j] - y[j]) ** 2 for j in range(len(y))) / len(y)
# 计算梯度
grad_w0 = 2 * sum(y_pred[j] - y[j] for j in range(len(y))) / len(y)
grad_w1 = 2 * sum((y_pred[j] - y[j]) * X[j][0] for j in range(len(y))) / len(y)
grad_w2 = 2 * sum((y_pred[j] - y[j]) * X[j][1] for j in range(len(y))) / len(y)
# 更新参数
w[0] -= lr * grad_w0
w[1] -= lr * grad_w1
w[2] -= lr * grad_w2
# 打印损失
if i % 100 == 0:
print(f"Iteration {i}: Loss = {loss}")
# 输出最终参数
print(f"Final parameters: w0 = {w[0]}, w1 = {w[1]}, w2 = {w[2]}")
逻辑回归
一元逻辑回归
之前所学的线性回归是为了拟合出一条直线/平面来拟合数据,以此达到预测数值的效果,而逻辑回归则不同,它是为了分类问题,以这里的一元逻辑回归为例:
| 气温 | 是否出门 |
|---|---|
| -10 | 0 |
| 3 | 1 |
| -3 | 0 |
| 5 | 1 |
| -4 | 0 |
| 7 | 1 |
| -6 | 0 |
| 8 | 1 |
以上是数据,当我们构造出图像时,如下所示

此时的他并不是一个具体的数值,而是非0即1的,这个时候我们就无法再使用线性回归来预测,所以就引进了逻辑回归来进行解决。
这里就引入了激活函数sigmoid,效果图如下
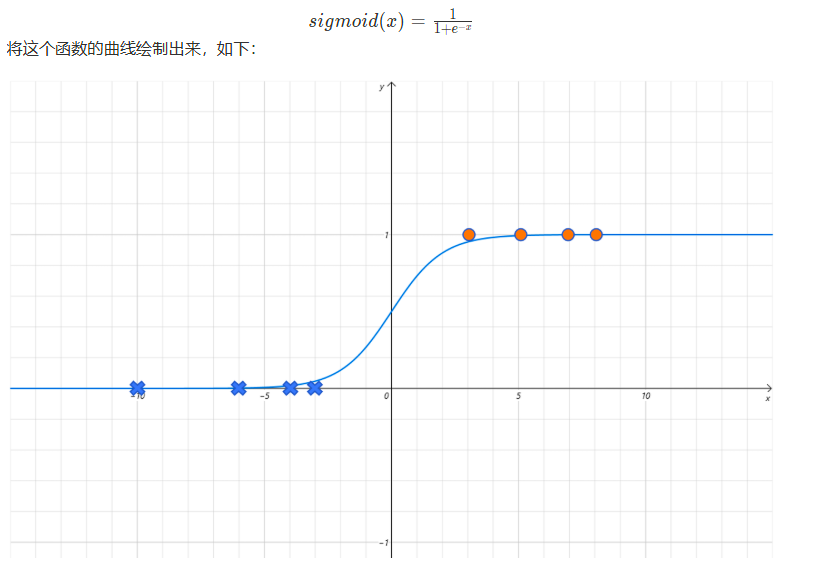
这里还不够拟合,所以我们可以在e-x前加入w,而后进行训练不断逼近即可。
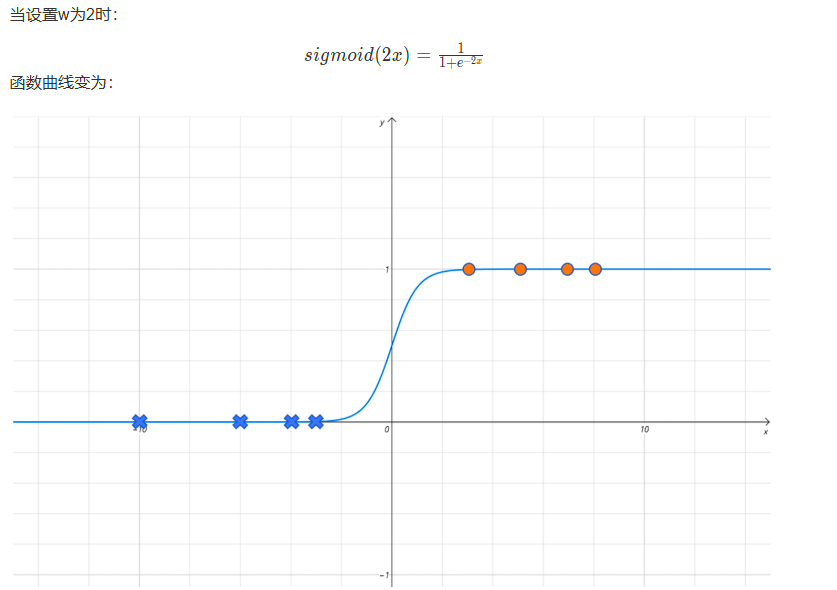
神经网络
梯度消失/爆炸
梯度消失是指,当参数进行多次迭代更新后,参数的变化已经变的微乎其微,比如100次的乘上0.1,这个数就会无比的小,贴近0,这个时候更新参数十分缓慢,这个就是梯度消失。
而梯度爆炸是指,当参数多次迭代后,由于导数值较大,比如100次的乘上1.2,这个数就会十分巨大,这会使我们的更新跳跃幅度过大,不利于更新。
卷积
当参数过多时,比如我们要处理一张灰白图片,他的大小是6*6*1,所以我们如果一个像素一个参数处理,就需要处理36个参数,而如果我们使用3*3的卷积核,对每个像素先进行卷积操作,最终就只剩下4*4*1的大小,而且我们只需要处理10个参数(3*3的卷积核+偏置b),就大大缩小了计算量,而且无论多少个像素,我们需要处理的参数也就只有这10个,因此,我们引入了卷积来处理图像。
其优点具体如下
1、图片输入特征多 图片输入特征多,但是一个3x3的卷积操作只有10个参数,就可以对整个图片进行扫描。
2、特征局部性 卷积操作的每个运算只在特定相邻区域内进行,并不要所有输入特征都参与运算。
3、平移不变性 卷积操作在整个图片上进行滑动检测,就是假设图片的特征具有平移不变性。
特征图的尺寸计算
对联分别的输出尺寸变化公式如下
输出尺寸 = (输入尺寸 - 卷积核大小 + 2*填充) / 步长 + 1
而有时会出现除不尽的情况,这个时候我们通常是进行向下取整来进行处理。
1*1卷积层
1*1卷积层存在的意义是他可以以最低成本改变通道数,示例如下
我们定义一个1x1卷积层,其卷积核的数量(即输出通道数)为 C_out。每个卷积核的尺寸是 [1, 1, C_in]。也就是说,每个卷积核都有 C_in 个权重值(每个输入通道对应一个权重)和一个偏置项。
这个1x1的窗口在特征图的空间维度(高度和宽度) 上滑动。因为窗口是1x1,所以它每次只“看”一个像素点。但是,这个像素点有 C_in 个通道,因此它看到的是一个包含 C_in 个数值的向量。
对于特征图上的每一个位置 (i, j),取出该位置所有 C_in 个通道的值,形成一个向量 [v1, v2, ..., v_Cin]。
用第一个1x1卷积核(它也有 C_in 个权重 [w1_1, w2_1, ..., w_Cin_1])与这个向量进行点积(即对应元素相乘后求和),再加上偏置,就得到了输出特征图在位置 (i, j) 的第一个通道的值。
输出值_1 = (v1 * w1_1) + (v2 * w2_1) + ... + (v_Cin * w_Cin_1) + 偏置_1
用第二个卷积核(权重为 [w1_2, w2_2, ...])与同一个输入向量再进行点积,得到输出特征图在 (i, j) 的第二个通道的值。
...
重复此过程,直到用完所有的 C_out 个卷积核。
经过上述操作,输入的 C_in 个通道的信息,在每个像素点上都被混合、加权,并投影到了一个全新的 C_out 维空间。
因为计算是在每个空间位置上独立、并行地完成的,所以输出的空间尺寸(高度和宽度)保持不变,但通道数从 C_in 变成了 C_out。
全局平均池化层
我们知道一般遇到的是最大池化层,从n*n的区域中拿出一个最大的值,即为最大池化操作,它只关注了局部的特征。而这里的全局平均池化是什么意思呢?
实际上,他就类似我们的平均数,比如当前有十个数,它就会求和再除10,这样就得到了全局平均池化的输出,这个不会引入额外参数,而且有每个像素的特征。
猫狗分类实战
import os
import random
from PIL import Image
from torchvision import transforms # ✅ 从 torchvision 导入
import torch
from torch import device, nn
from torch.utils.data import DataLoader, Dataset, TensorDataset
def verify_images(image_folder):
classes = ["Cat", "Dog"]
class_to_idx = {"Cat": 0, "Dog": 1}
samples = []
for cls_name in classes:
cls_dir = os.path.join(image_folder, cls_name)
for fname in os.listdir(cls_dir):
if not fname.lower().endswith(('.jpg', '.jpeg', '.png')):
continue
path = os.path.join(cls_dir, fname)
try:
with Image.open(path) as img:
img.verify()
samples.append((path, class_to_idx[cls_name]))
except Exception:
print(f"Warning: Skipping corrupted image {path}")
return samples
class ImageDataset(Dataset):
def __init__(self, samples, transform=None):
self.samples = samples
self.transform = transform
def __len__(self):
return len(self.samples)
def __getitem__(self, idx):
path, label = self.samples[idx]
with Image.open(path) as img:
img = img.convert("RGB")
if self.transform:
img = self.transform(img)
return img, label
class CNNmodel(nn.Module):
def __init__(self):
super().__init__()
self.model = nn.Sequential(
nn.Conv2d(3, 16, 3, padding=1),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(16, 32, 3, padding=1),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(32, 64, 3, padding=1),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(64, 128, 3, padding=1),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(128,1,1),
nn.AdaptiveAvgPool2d(1),
nn.Flatten(),
nn.Sigmoid()
)
def forward(self, x):
return self.model(x)
def evaluate(model,test_dataloader):
model.eval()
val_correct = 0
val_total = 0
with torch.no_grad():
for inputs,labels in test_dataloader:
inputs = inputs.to(device)
labels = labels.float().unsqueeze(1).to(device)
outputs = model(inputs)
preds = (outputs >= 0.5).float()
val_correct += (preds == labels).sum().item()
val_total += labels.size(0)
val_acc = val_correct / val_total
return val_acc
if __name__ == "__main__":
DATA_DIR = r"D:\Computer Graphic\review\examples\datasets\archive\PetImages"
BATCH_SIZE = 64
IMG_SIZE = 128
EPOCHS = 10
LR = 0.001
PRINT_STEP = 100
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
all_samples = verify_images(DATA_DIR)
random.seed(42)
random.shuffle(all_samples)
train_size = int(len(all_samples) * 0.8)
train_samples = all_samples[:train_size]
valid_samples = all_samples[train_size:]
data_transform = transforms.Compose([
transforms.Resize((IMG_SIZE,IMG_SIZE)),#统一图片大小
transforms.ToTensor(),#转换为张量
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]) #标准化
])
train_dataset = ImageDataset(train_samples,data_transform)
valid_dataset = ImageDataset(valid_samples,data_transform)
train_dataloader = DataLoader(train_dataset, batch_size=BATCH_SIZE, shuffle=True,num_workers=4)
valid_dataloader = DataLoader(valid_dataset, batch_size=BATCH_SIZE, shuffle=False,num_workers=4)
model = CNNmodel().to(device)
criterion = nn.BCELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=LR)
for epoch in range(EPOCHS):
print(f"\nEpoch {epoch+1}/{EPOCHS}")
model.train()
running_loss = 0.0
for step,(inputs,labels) in enumerate(train_dataloader):
inputs = inputs.to(device)
labels = labels.float().unsqueeze(1).to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if (step + 1) % PRINT_STEP == 0:
avg_loss = running_loss / PRINT_STEP
print(f"Step {step+1}- Loss: {avg_loss:.4f}")
running_loss = 0.0
val_acc = evaluate(model, valid_dataloader)
print(f"Validation Accuracy after epoch {epoch+1}: {val_acc:.4f}")
图像增强
什么是图像增强,图像增强是在保持图像语义不变的情况下,生成多样化的新数据。例如旋转,裁剪,颜色亮度等的改变,都是图像增强的一种方式。
几何变化
旋转,这个是我们所熟悉的操作,将物体按照一定角度进行旋转操作后,表达语义仍然不变。

那么如何在PyTorch里实现旋转操作呢,具体如下。
首先我们定义一个函数,它可以对图片应用PyTorch里Transform对象的操作,进而展示图片。
def imshow(img_path,transform):
img = Image.open(img_path)
fig,ax = plt.subplots(1,2,figsize=(15,4))
ax[0].set_title(f"Original Image {img.size}")
ax[0].imshow(img)
img = transform(img)
ax[1].set_title(f"Transformed Image {img.size}")
ax[1].imshow(img)
plt.show()
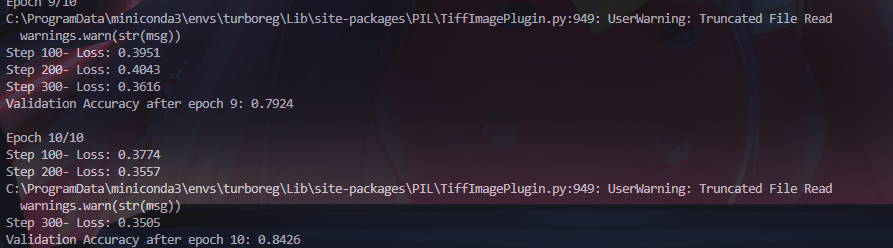
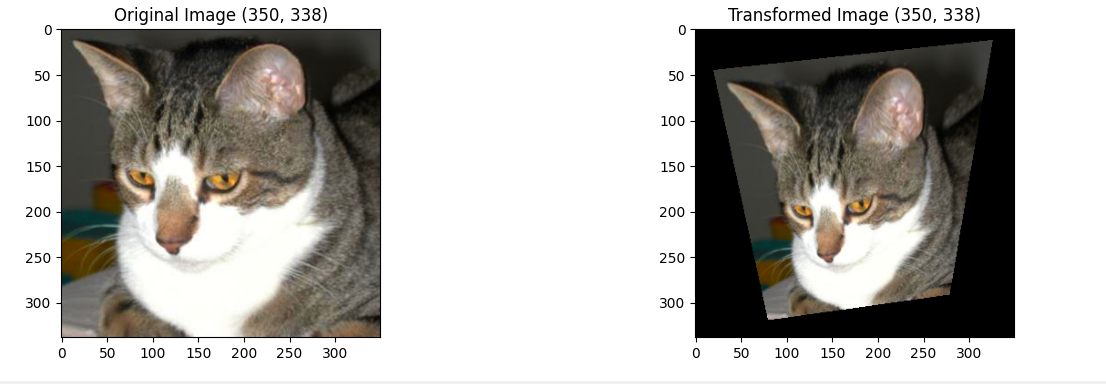
而后通过以下代码即可实现在-30-30度之间随机旋转
path = r"D:\Computer Graphic\review\examples\datasets\archive\PetImages\Cat\238.jpg"
transform = transforms.RandomRotation(degrees=30)
imshow(path,transform)
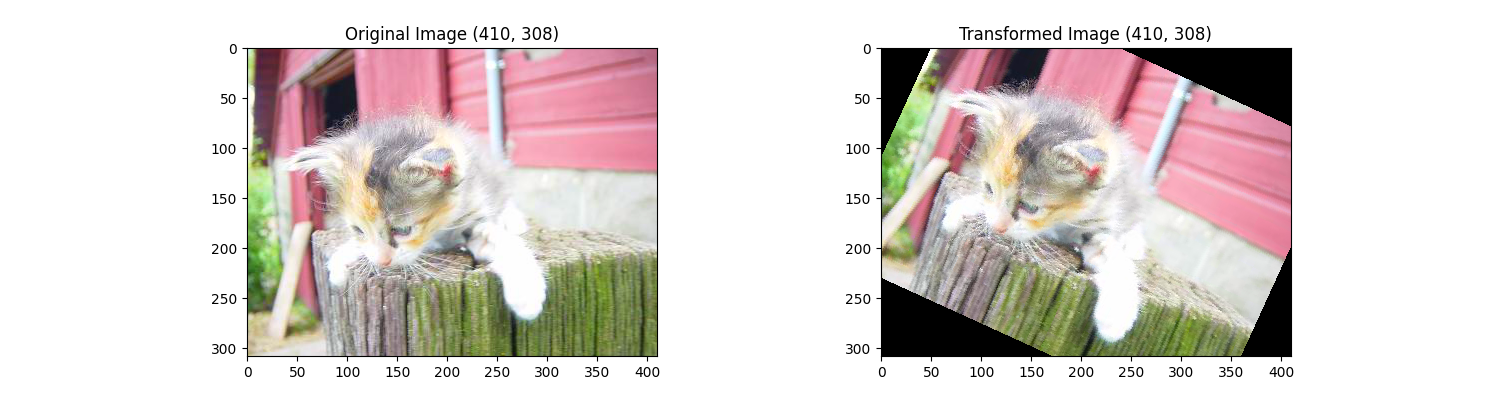
翻转
具体有水平和垂直,水平如下
path = r"D:\Computer Graphic\review\examples\datasets\archive\PetImages\Cat\2239.jpg"
transform = transforms.RandomHorizontalFlip(p=1.0)#p代表翻转概率
imshow(path,transform)
垂直翻转如下
transform = transforms.RandomVerticalFlip(p=1.0)
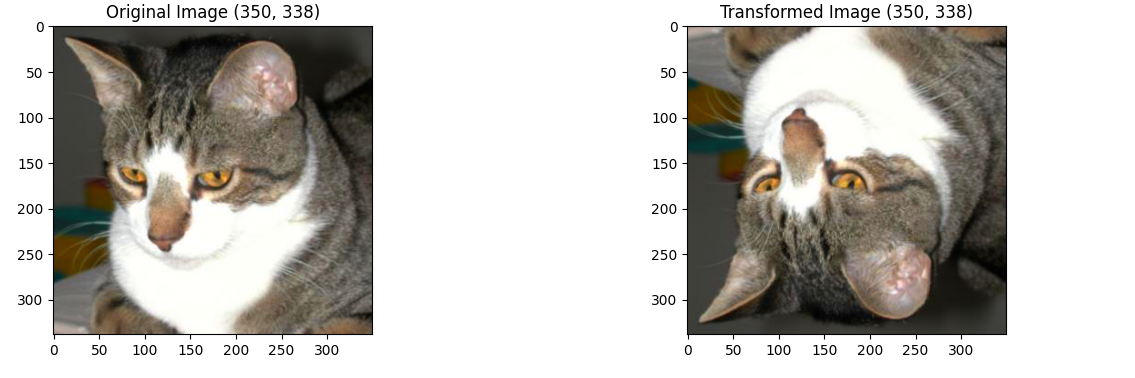
裁剪
不难理解,随机裁剪出图像区域
transform = transforms.RandomCrop(size=(120, 120))

透视变换
改变图片的形状,进行一定的角度扭曲
transform = transforms.RandomPerspective(
distortion_scale=0.5, # 控制变形强度,0~1,越大越扭曲
p=1.0, # 应用该变换的概率
interpolation=transforms.InterpolationMode.BILINEAR
)
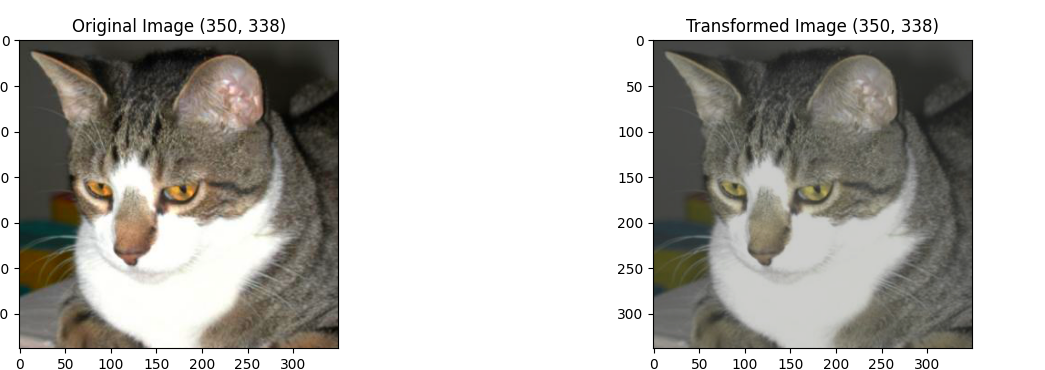
颜色变化
颜色具体可调的是亮度、对比度、饱和度和色调
transforms.ColorJitter(
brightness=0.5,#图像亮暗程度,设置为x时从[1-x,1+x]随机旋转
contrast=0.5,#图像对比度,范围[1-x,1+x]
saturation=0.5,#图像饱和度,范围[1-x,1+x]
hue=0.1#色调,范围[-0.5,0.5],设置为0.1则为[-0.1,0.1]
)
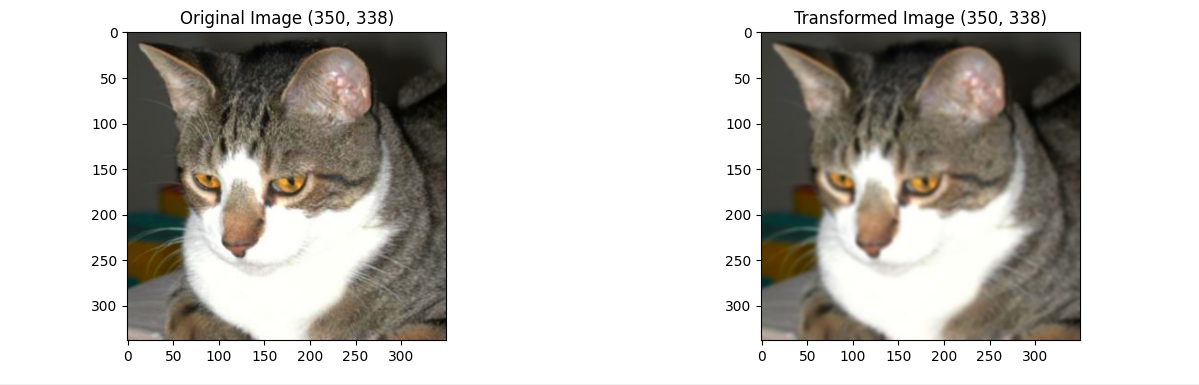
模糊
对图像进行高斯模糊
# 对图像进行高斯模糊,kernel size 为 5,sigma 可调节模糊强度
transform = transforms.GaussianBlur(kernel_size=5, sigma=(0.1, 3.0))
其中kernel_size是指高斯模糊卷积核的大小,它决定模糊的范围,必须为奇数,设置越大则模糊效果越明显。后面传入的元组(0.1,3.0),表示在里面随机旋转一个值,sigma越大越模糊
遮罩
遮罩是指随机遮挡一个或多个连续的方形区域,让模型忽略局部信息更关注上下文特征,有利于提升模型鲁棒性。
PyTorch里没有直接实现,这里需要自己进行实现
from PIL import Image
import numpy as np
import random
def cutout_pil_multi(image, mask_size=50, num_masks=3):
"""
对图像应用多个 Cutout 遮挡块
参数:
- image: PIL.Image 对象
- mask_size: 每个遮挡块的大小(正方形边长)
- num_masks: 遮挡块的数量
"""
image_np = np.array(image).copy()
h, w = image_np.shape[0], image_np.shape[1]
for _ in range(num_masks):
y = random.randint(0, h - 1)
x = random.randint(0, w - 1)
y1 = max(0, y - mask_size // 2)#防止变为负数
y2 = min(h, y + mask_size // 2)#防止溢出
x1 = max(0, x - mask_size // 2)
x2 = min(w, x + mask_size // 2)
# 遮挡区域设置为黑色
image_np[y1:y2, x1:x2, :] = 0
return Image.fromarray(image_np)
而后调用函数即可
imshow(path, cutout_pil_multi)

这个时候我们就可以利用已有的图像增强技术给猫狗分类实战加上,相当于扩充了训练集。
train_transform = transforms.Compose([
transforms.Resize((150,150)),
transforms.RandomCrop(size=(IMG_SIZE,IMG_SIZE)),
transforms.RandomHorizontalFlip(p=0.5),
transforms.ColorJitter(
brightness=0.5,
contrast=0.3,
saturation=0.4,
hue=0.1
),
transforms.RandomRotation(degrees=15),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
valid_transform = transforms.Compose([
transforms.Resize((IMG_SIZE,IMG_SIZE)),#统一图片大小
transforms.ToTensor(),#转换为张量
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]) #标准化
])
train_dataset = ImageDataset(train_samples,train_transform)
valid_dataset = ImageDataset(valid_samples,valid_transform)
语义分割
什么是语义分割呢,将图片所有的像素都赋予语义信息的任务就是语义分割,如下图所示

循环神经网络(RNN)
循环神经网络常用于序列问题,序列问题是指数据之间存在顺序的问题,输入、输出或两者都是有序的数据序列,元素上存在时间或位置上的联系,在考虑这类问题时,我们需要考虑前面/未来的信息。
事实上,他的工作方式如下图所示
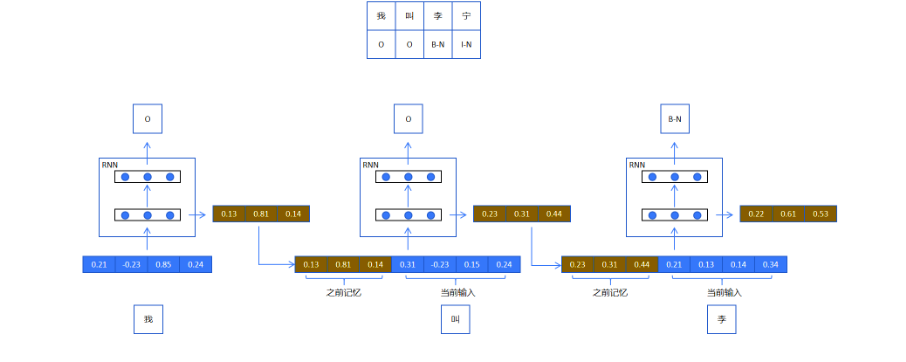
它会将上一层的隐藏层输出,传给下一层的输入,将这两个拼接就组成了下一个的输入,然后传入隐藏层再到输出层得到预测结果,之后循环往复,直至最终。
由此可得当前隐状态的计算公式
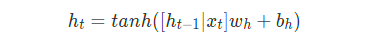
其中,xt表示t时刻输入,yt表示t时刻输出,ht表示t时刻更新后记忆,即隐状态。wh表示隐藏层权重,bh表示隐藏层偏置,wy表示输出层权重,by表示输出层偏置。
输出层使用了Softmax函数作为激活函数
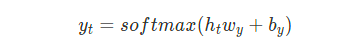
通过观测可以得出,其实只有第一层隐藏层我们在循环使用,第二层是普通层,因此第一层也被我们称为循环层。循环层的递归调用就是RNN的本质。每一时间步对之前所有的时间步的循环层的调用,输出关键隐状态ht。对于普通层,可以看成是每一时间步利用ht向量作为输入,进行的额外的分类或者回归任务。普通层不是RNN的核心,它只是为了完成每一步的特定任务添加的任务层。
LSTM
之前的RNN只能记住前一时刻的信息,只有短时记忆,而在现实生活中例如语音识别、天气预报、股票预测这些情况下我们都需要进行长期时间的记忆,这个时候我们就引入了长短期记忆网络(LSTM)。
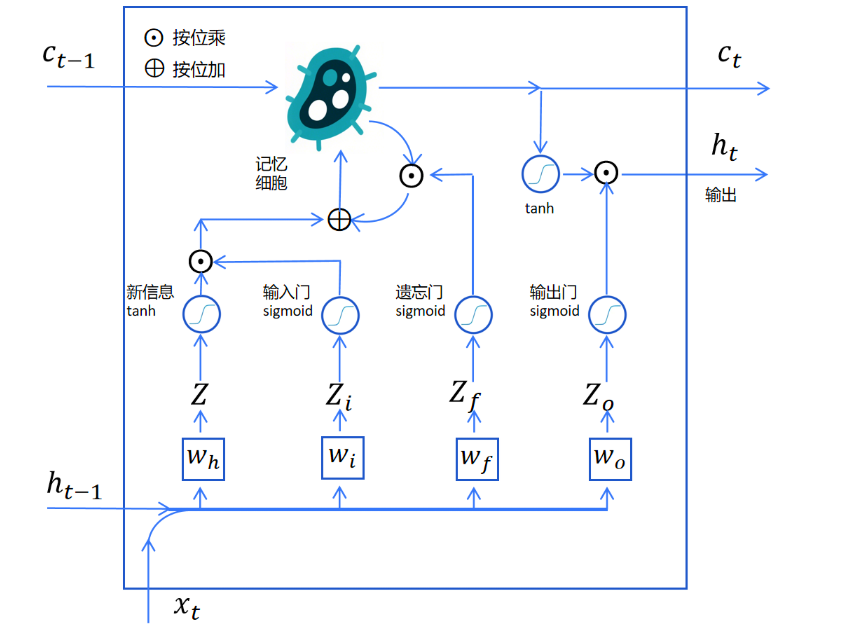
我们对新输入的信息进行存储作为Z,而后再传入上一时间状态的Ht-1和这一时刻的信息Xt,经过sigmoid函数作为输入门,即输入信息的控制函数,将Z和这个相乘得到新的输入,此操作将判定一部分新信息可以进入记忆,一部分则被丢弃。这个时候它就是受控新信息,接下来他就该进入长时记忆了,那么如何进入长时记忆呢,这里我们首先需要取出长时记忆,然后选择一部分需要遗忘的记忆,以此来给出空间存储新的记忆,这个时候依然使用sigmoid函数作为遗忘门函数进行筛选,然后将长期记忆乘上遗忘门的函数再加上tanh激活函数处理的新信息Z乘上控制函数,作为待输出记忆,也就是要存储的长期记忆,而后对这部分再进行tanh激活函数处理,再经过sigmoid输出门处理,判断那部分需要输出,得到的输出就是隐状态的输出了。多个时间步就是以Ct-1作为前一步的长时记忆,经过当前时间步处理后,生成新的长时记忆Ct和隐状态ht,传至下一个记忆中心。公式如下所示

不过这里的wh、wi、wo实际上都是两个权重,以wh为例,我们的wh包含了前一时刻ht-1隐状态输出的权重wh,还包含了这一时刻输入xt的权重wx
代码实现如下
import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
def get_lstm_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device)*0.01
def three():
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xi, W_hi, b_i = three() # 输入门参数
W_xf, W_hf, b_f = three() # 遗忘门参数
W_xo, W_ho, b_o = three() # 输出门参数
W_xc, W_hc, b_c = three() # 候选记忆元参数
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
b_c, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
W_hq, b_q] = params
(H, C) = state
outputs = []
for X in inputs:
I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)
F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)
O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)
C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)
C = F * C + I * C_tilda
H = O * torch.tanh(C)
Y = (H @ W_hq) + b_q
outputs.append(Y)
return torch.cat(outputs, dim=0), (H, C)
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,
init_lstm_state, lstm)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
GRU
GRU,即门控循环单元,他相较LSTM变得更加精简了一些,他只有重置门和更新门,去除了LSTM的记忆细胞,也实现了记录长时记忆和更新的效果。
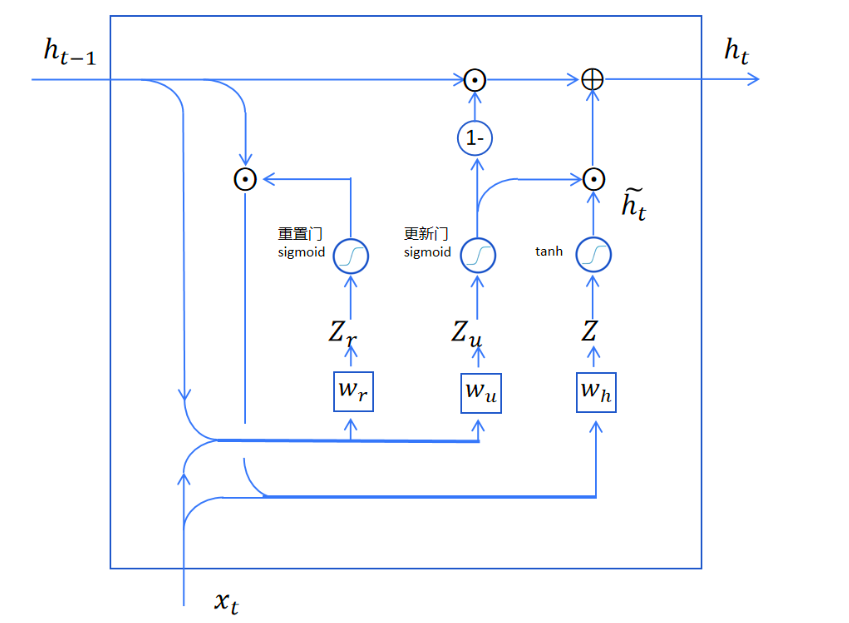
这里通过重置门实现遗忘部分信息,这里的重置门实际上就是LSTM的遗忘门,他将上一时刻的记忆ht-1和当前时刻的输入Xt进行拼接,而后经过线性层,再加上偏置进行sigmoid激活函数处理,就得到了Gr。
这个得到的Gr再乘上ht-1,就是我门经过重置后的长时记忆。重置后的长期记忆和当前输入xt合并,然后经过一个线性层(权重为wh),加tanh激活,就得到当前层的备用输出ht~。
此时得到的备用输出还是无法直接输出,因为GRU只能靠隐状态来传递长时记忆,这里需要将长期保留的记忆加进来再作为当前时间步的隐状态作为输出。这里怎样决定哪些维度保留长期记忆,哪些维度作为备用输出的隐状态呢,答案是使用更新门函数进行处理,这个函数同时决定保留多少长期记忆,更新多少当前步产生的记忆。
首先用sigmoid更新门生成一个更新向量,而后和备用输出相乘,获得要更新到长期记忆里的信息。然后用1减去更新向量,这样就得到了对长期记忆的保留向量。用保留向量与长期记忆按位点乘,就得到了保留的长期记忆,在和更新信息相加,就得到了这一步输出的长期记忆,ht。

其实现代码如下
import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
def get_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device)*0.01
def three():
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xz, W_hz, b_z = three() # 更新门参数
W_xr, W_hr, b_r = three() # 重置门参数
W_xh, W_hh, b_h = three() # 候选隐状态参数
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
def init_gru_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), )
def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = H @ W_hq + b_q
outputs.append(Y)
return torch.cat(outputs, dim=0), (H,)
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_params,
init_gru_state, gru)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
深度循环神经网络
之前的都是只有一层隐藏层,而这里则是指使用多层隐藏层,每个隐状态都连续地传递到当前层的下一个时间步和下一层的当前时间步。
它与之前的LSTM代码几乎一致,唯一不同的是这里多加了隐藏层,之前我们得到隐状态后即为结束,这里需要传到下一个隐藏层。
import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
def get_multi_lstm_params(vocab_size, num_hiddens, num_layers, device):
"""初始化多层LSTM参数"""
num_inputs = vocab_size
num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device) * 0.01
def three(in_size, out_size):
"""返回门控机制的三组参数"""
return (normal((in_size, out_size)),
normal((out_size, out_size)),
torch.zeros(out_size, device=device))
params = []
# 初始化各层参数
for i in range(num_layers):
# 第一层输入为vocab_size,其他层输入为上一层的隐藏层大小
in_size = num_inputs if i == 0 else num_hiddens
# 输入门、遗忘门、输出门、候选记忆元参数
W_xi, W_hi, b_i = three(in_size, num_hiddens)
W_xf, W_hf, b_f = three(in_size, num_hiddens)
W_xo, W_ho, b_o = three(in_size, num_hiddens)
W_xc, W_hc, b_c = three(in_size, num_hiddens)
params.extend([W_xi, W_hi, b_i, W_xf, W_hf, b_f,
W_xo, W_ho, b_o, W_xc, W_hc, b_c])
# 输出层参数(连接最后一层隐藏层到输出)
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
params.extend([W_hq, b_q])
# 开启梯度计算
for param in params:
param.requires_grad_(True)
return params
def init_multi_lstm_state(batch_size, num_hiddens, num_layers, device):
"""初始化多层LSTM的隐藏状态和记忆元"""
return [(torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))
for _ in range(num_layers)]
def multi_lstm(inputs, state, params, num_layers):
"""多层LSTM前向传播"""
# 解析状态:每层包含(H, C)
layer_states = state
outputs = []
# 每层参数数量:12个参数(4个门×3组参数)
per_layer_params = 12
current_inputs = inputs
# 逐层计算
for layer in range(num_layers):
layer_params = params[layer * per_layer_params : (layer + 1) * per_layer_params]
H, C = layer_states[layer]
layer_outputs = []
# 时序步计算
for X in current_inputs:
# 输入门
I = torch.sigmoid((X @ layer_params[0]) + (H @ layer_params[1]) + layer_params[2])
# 遗忘门
F = torch.sigmoid((X @ layer_params[3]) + (H @ layer_params[4]) + layer_params[5])
# 输出门
O = torch.sigmoid((X @ layer_params[6]) + (H @ layer_params[7]) + layer_params[8])
# 候选记忆元
C_tilda = torch.tanh((X @ layer_params[9]) + (H @ layer_params[10]) + layer_params[11])
# 更新记忆元
C = F * C + I * C_tilda
# 更新隐藏状态
H = O * torch.tanh(C)
layer_outputs.append(H)
# 当前层输出作为下一层输入
current_inputs = layer_outputs
# 更新该层状态
layer_states[layer] = (H, C)
# 输出层计算(使用最后一层的输出)
W_hq, b_q = params[-2], params[-1]
final_outputs = [(H @ W_hq) + b_q for H in current_inputs]
return torch.cat(final_outputs, dim=0), layer_states
# 模型超参数
vocab_size = len(vocab)
num_hiddens = 256 # 每层隐藏单元数
num_layers = 2 # 隐藏层数(可根据需要调整)
device = d2l.try_gpu()
num_epochs, lr = 500, 1 # 多层网络可能需要调整学习率和迭代次数
# 定义模型
def model_fn(vocab_size, num_hiddens, device, num_layers):
return d2l.RNNModelScratch(
vocab_size, num_hiddens, device,
lambda vs, nh, dev: get_multi_lstm_params(vs, nh, num_layers, dev),
lambda bs, nh, dev: init_multi_lstm_state(bs, nh, num_layers, dev),
lambda inputs, state, params: multi_lstm(inputs, state, params, num_layers)
)
model = model_fn(vocab_size, num_hiddens, device, num_layers)
# 训练模型
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
注意力机制
Self-attention
这里的自注意力机制是一对一的,即每一个向量vector输入,就会输出一个对应的标签label

使用全连接层完成输出,但是我们要考虑前后文,怎么做呢,我们可以一次选定Window大小,可以连接上下文。但是如果Sequence过长,我们的Window设置很大的话,计算量将十分巨大,所以这个时候就用到了self-attention
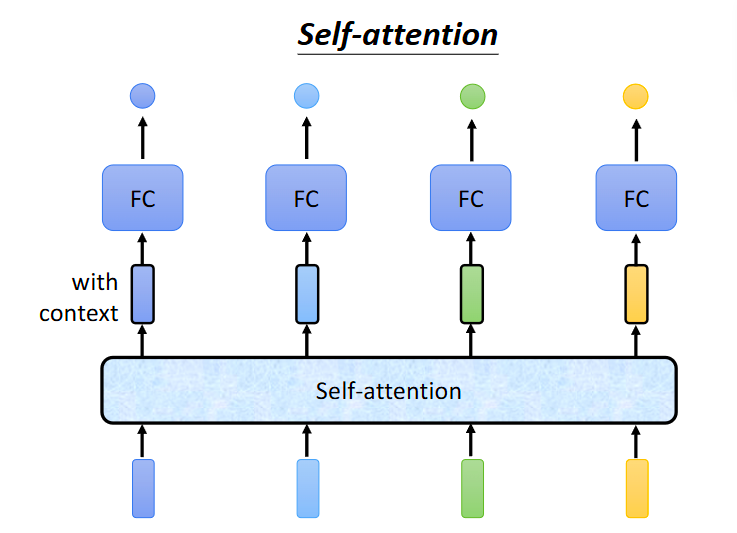
Self-attention一次将读取全部的输入,然后再进行输出,同时这个也可以进行叠加,叠加多次再生成输出。具体计算如下
生成b1:
- a1与其他向量的关联性α
α计算方法:
(1)dot-product:输入向量分别乘两个矩阵Wq和Wk,产生的q和k点乘得到α(最常用,用在transformer里面)
(2)additive:得到的q与k相加通过激活函数activate function然后通过transform?得到α
| 方法 | 公式 | 特点 |
|---|---|---|
| Dot-product | α = qᵀ·k |
计算简单,效率高,最常用 |
| Additive | α = vᵀ·tanh(W·[q;k]) |
更灵活,可处理不同维度的q,k |
这里我们采用的是第一种方法。
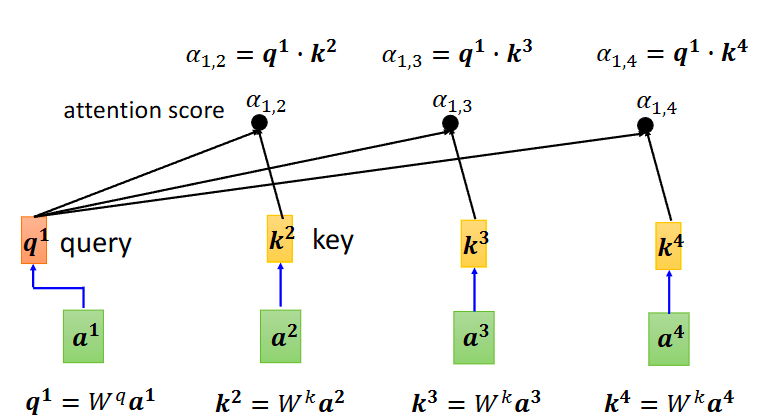
实际上自己也会和自己做关联性,这样做的意义是保留自身信息,如果不计算α1,1,输出b1就会由其他向量决定,该操作就类似于人在做选择时,既要倾听他人建议,同时也要考虑自身的想法。

然后用Softmax函数对α进行处理
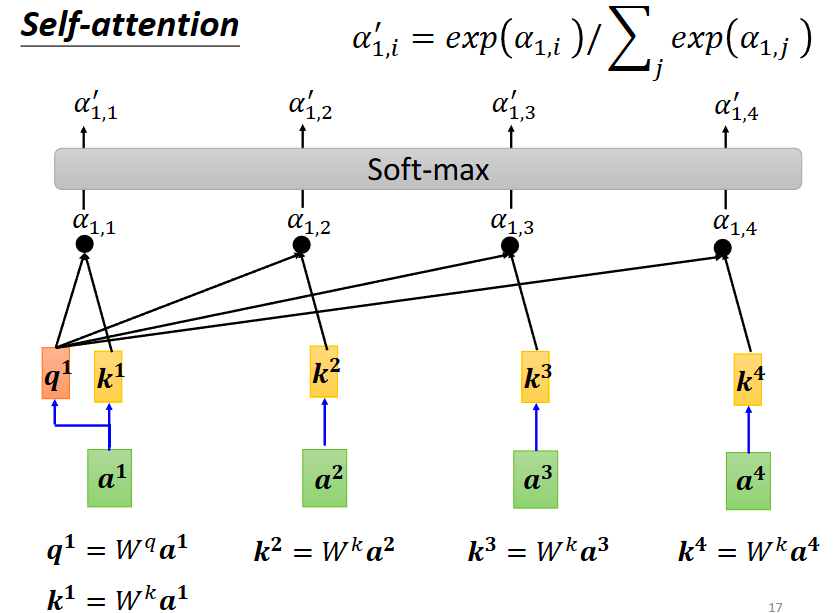
接下来再乘上通过a*Wv得到v,v与α相乘就得到了最终的b1
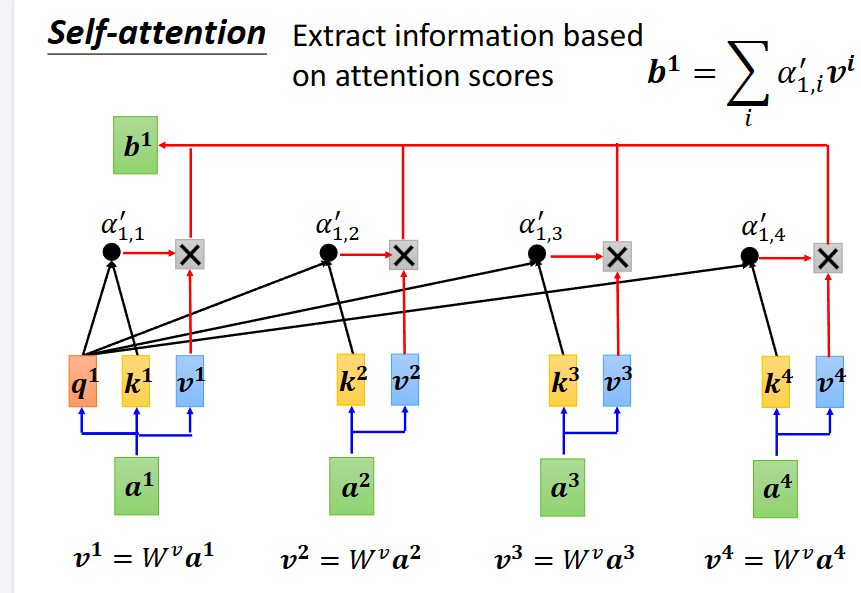
如果a1,a2关联性很强,那么b1就可能会比较接近b2。
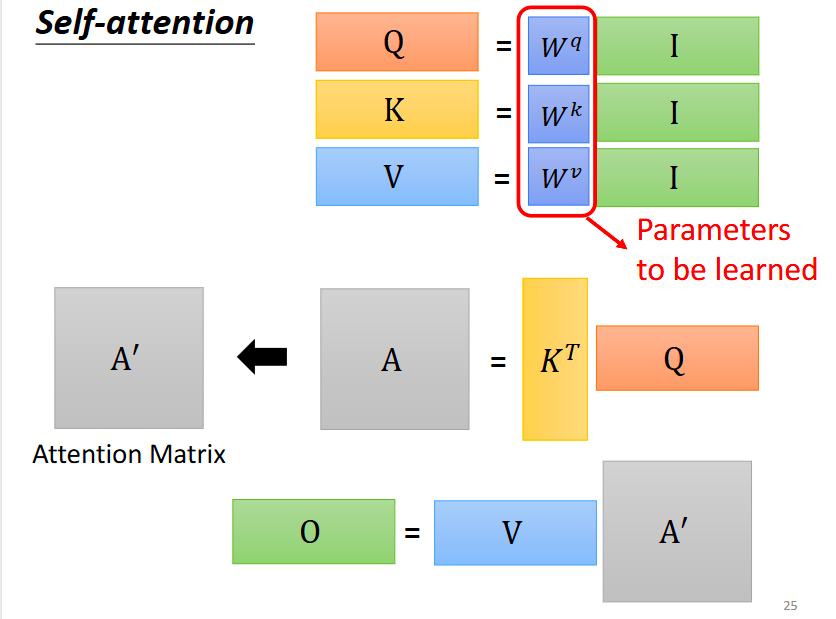
将输入向量和QKV这些都视为矩阵,可以发现实际上只有三个参数是我们未知的,Wq、Wk和Wv
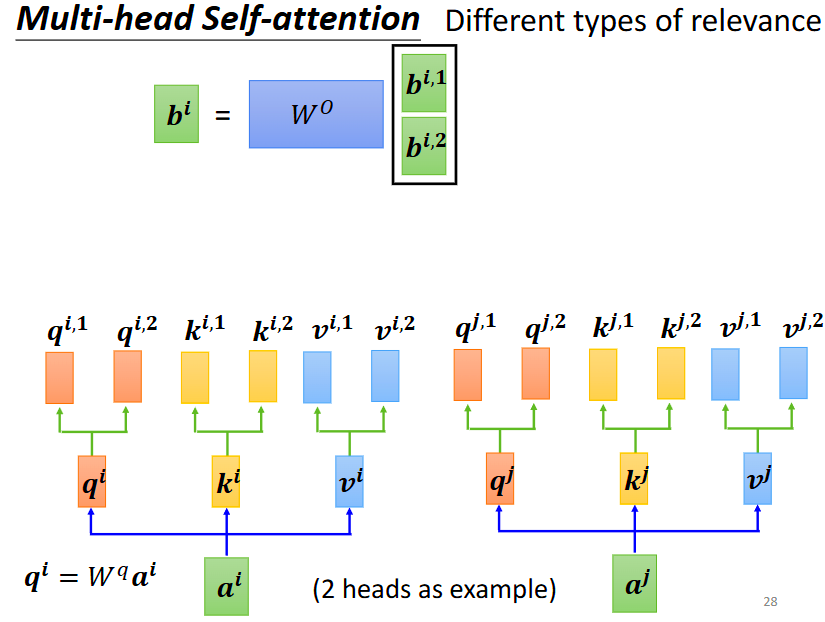
多头注意力机制
多头注意力机制与自注意机制类似,只是它有多个qkv
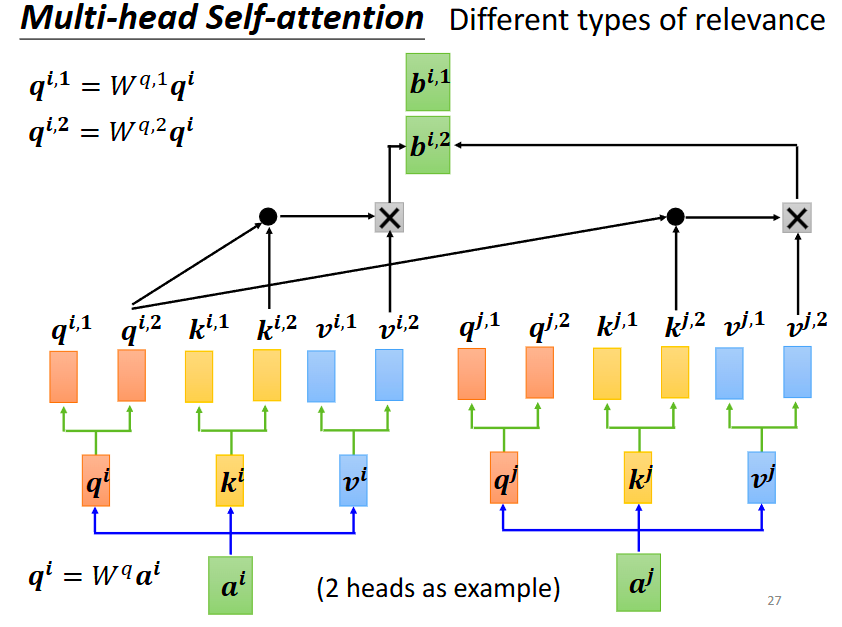
我们这里计算依旧从前,不过我们计算bi1就只考虑ki,1和vi,1这些部分,计算bi2就只考虑qi2,ki2,vi2这部分,最终计算的时候将bi,1和bi,2视为一个矩阵进行计算,得到最终的bi。
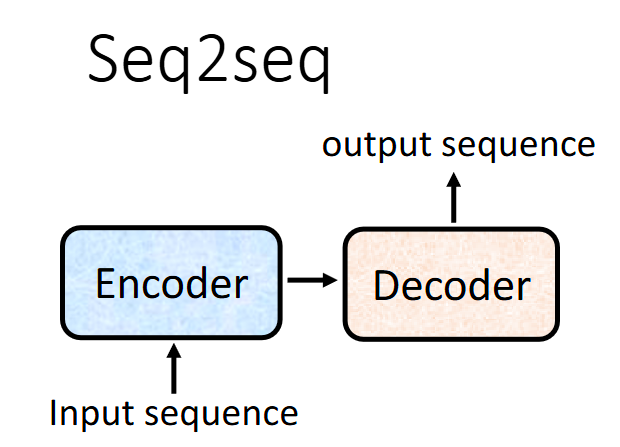
Transfrom
Transfrom采用的结构是Sequence to Sequence,缩写为Seq2Seq,如下图所示
Encoder
encoder可以用rnn/cnn/self attention,编码的目的就是,输入一排向量,输出一排等同数量的向量。
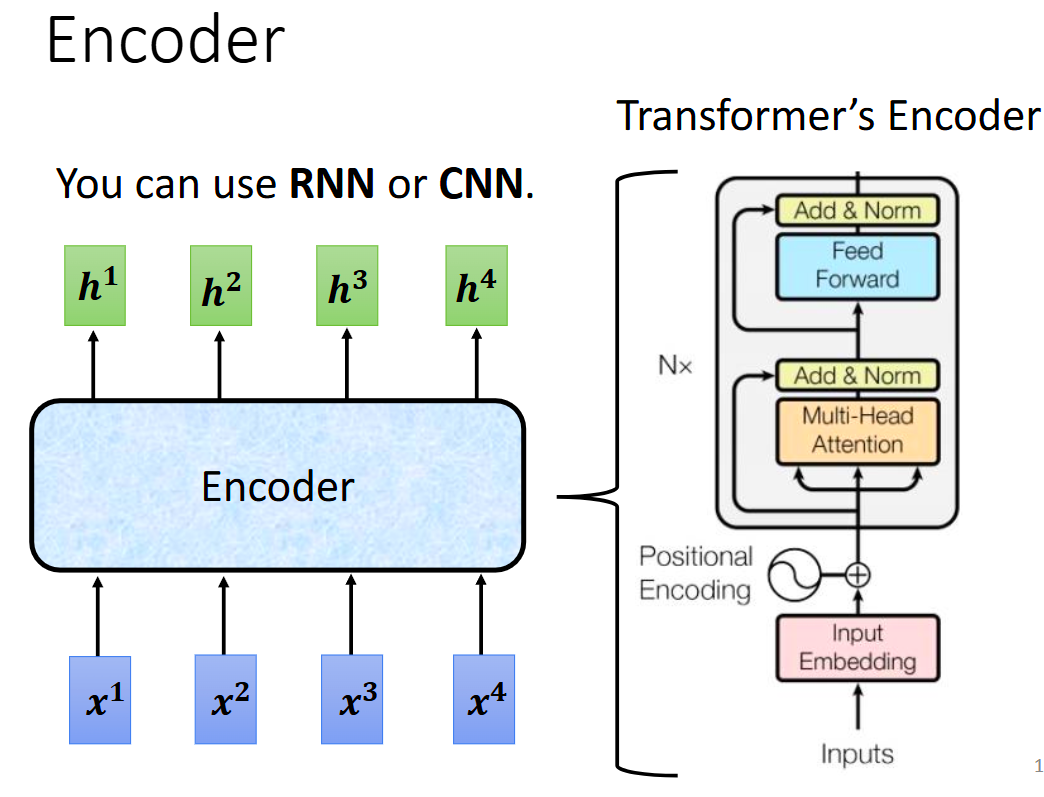
Encoder结构具体可分为以下部分
1、输入层
负责接收输入序列,并将每个符号(如单词)转换为一个向量表示。这个向量表示通常被称为词嵌入(embedding),它是通过学习大量语料库而得到的。
2、位置编码层(positonal encoding)
由于Transformer模型采用自注意力机制,它不像RNN那样天然地考虑输入序列中词的位置信息。因此,位置编码层负责将每个词的位置信息编码为一个向量,并将其加到词嵌入上。这样,模型就能考虑到词在序列中的位置。
3、编码器层堆叠(block)
Transformer模型的Encoder部分通常由多个编码器层堆叠而成。每个编码器层都具有相同的结构block,并且它们之间通过残差连接和规范化层进行连接。
4、多头自注意力子层(multi head attention)
在每个编码器层中,首先是一个多头自注意力子层。这个子层负责计算输入序列中每个词与其他词之间的相关性,并生成一个注意力权重分布。这个注意力权重分布用于计算一个加权和的向量表示,这个向量表示考虑了序列中其他词对当前词的影响。
5、前馈全连接子层(feed forward)
在每个编码器层中,紧接着多头自注意力子层的是一个前馈全连接子层。这个子层负责将多头自注意力子层的输出通过一个全连接神经网络进行处理,以捕获更复杂的特征表示。
6、残差连接和规范化层
在每个子层之后,都有一个残差连接和一个规范化层。残差连接负责将子层的输入与输出相加,以避免梯度消失和表示瓶颈问题。规范化层则负责对子层的输出进行规范化处理,以加速模型的收敛速度。
Block结构如下图所示
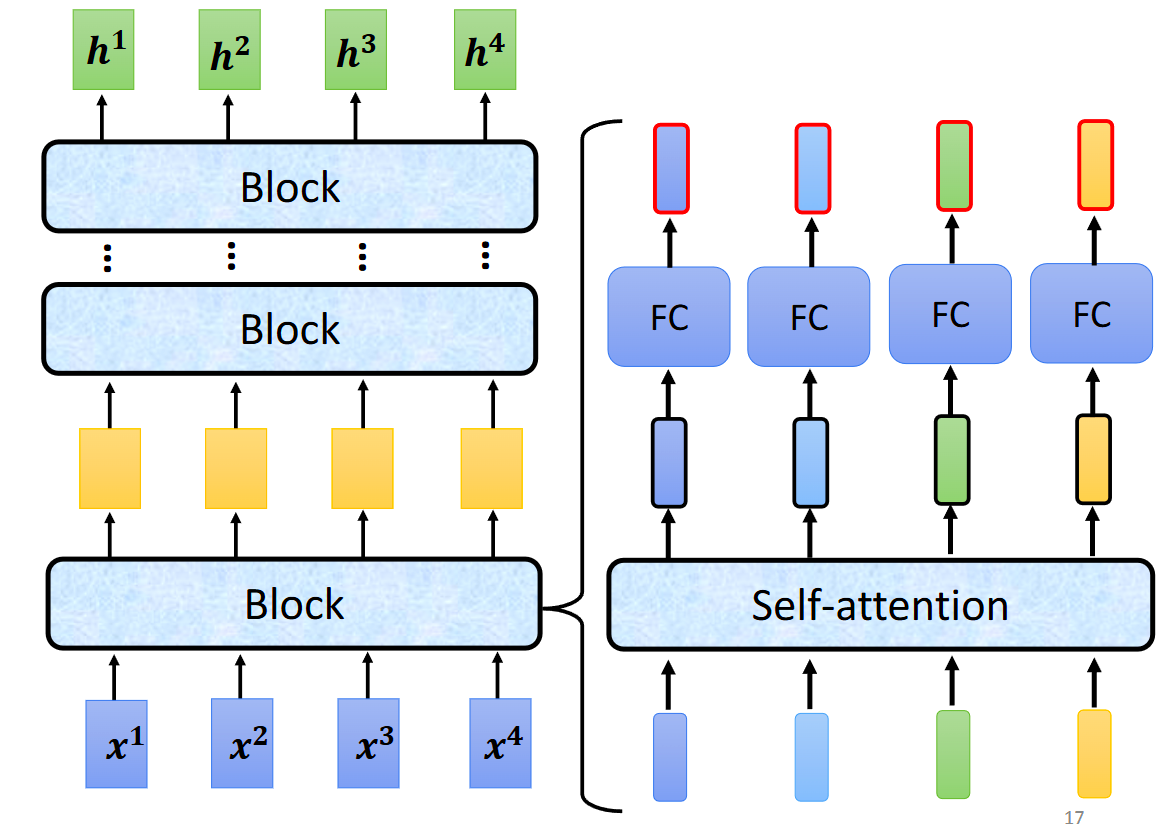
其中,一个block包含了以下
(1)self-attention
(2)feed forward(在李宏毅的课件里称为FC)
(3)residual
(4)norm
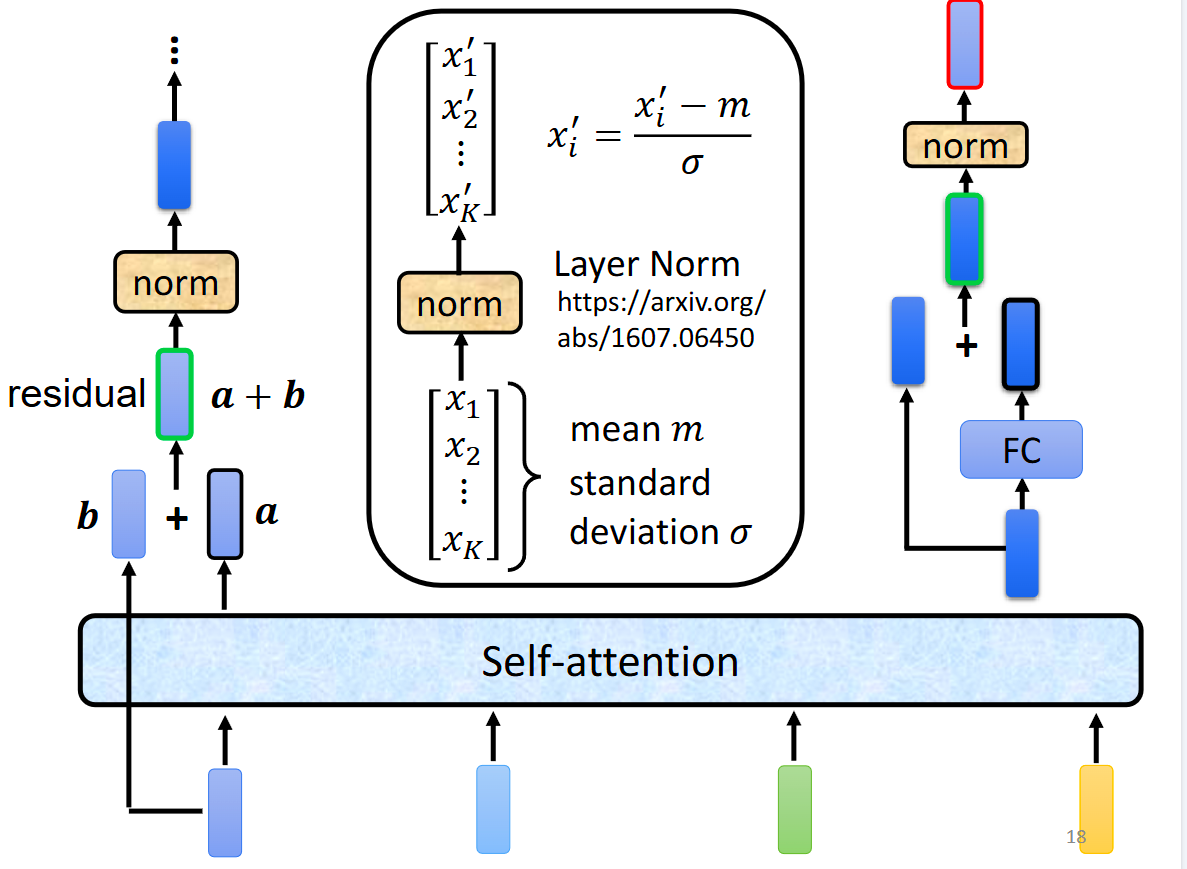
self-attention子层中的residual connection(残差连接)被用来添加输入数据和输出数据之间的直接连接(输入和输出相加一次),作用如下
(1)避免梯度消失或梯度爆炸问题;
(2)残差连接可以使输入数据和输出数据的形状保持不变,避免信息丢失,并且可以使模型的训练速度和精度得到提高。
得到residual后对其进行normalization(layer normalization,这个是计算一整个样本的标准化方式)。
norm完后,在全连接层层也进行residual。
residual后,再norm,最后得到一个block的输出。
Decoder
Decoder实际上与Encoder十分相像,遮挡中间的一部分,可以发现除了最后的Decoder走了线性层和Softmax,两者在前面的操作几乎无二。
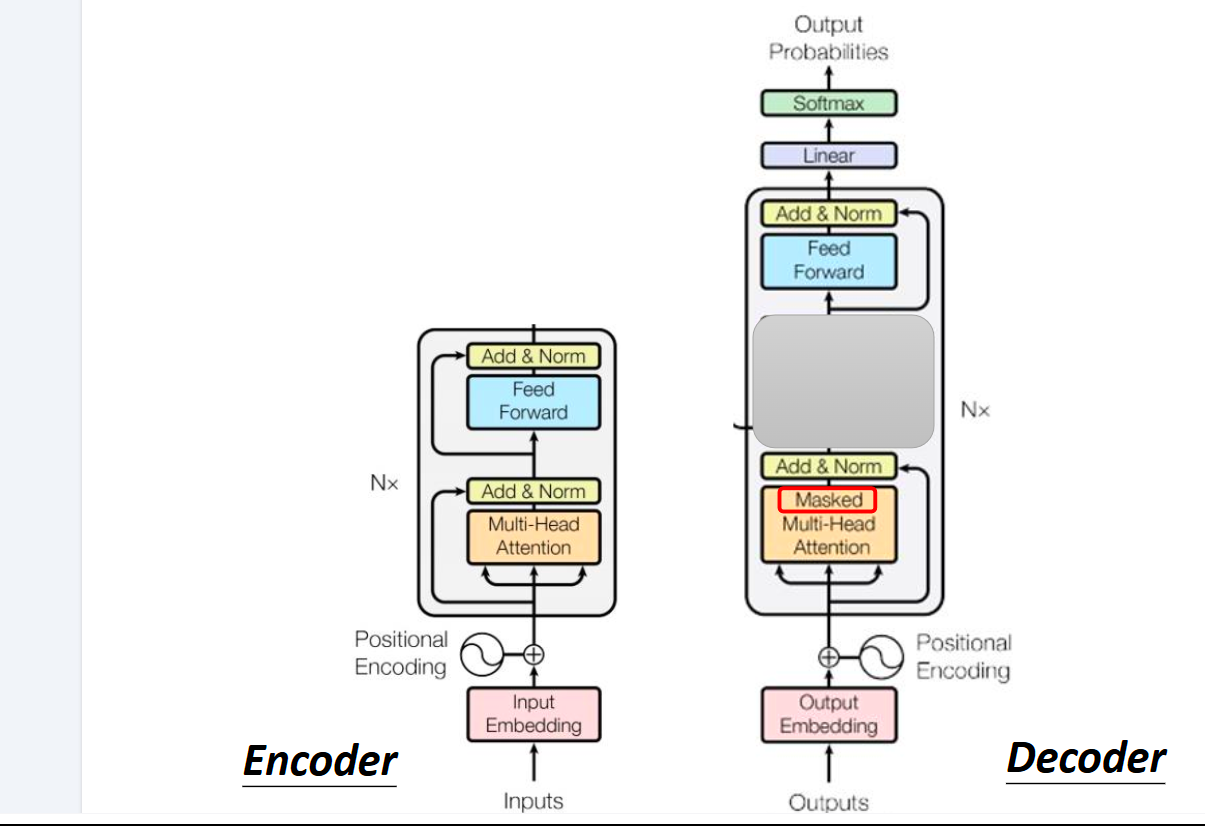
需要注意的是这里的多头注意力机制是加了Masked的,这个是什么意思呢。因为是一个一个输入的,比如当前要计算α2,我们还不知道a3和a4,那我们就只计算a1和a2,而不再考虑a3,a4。
完整的结构
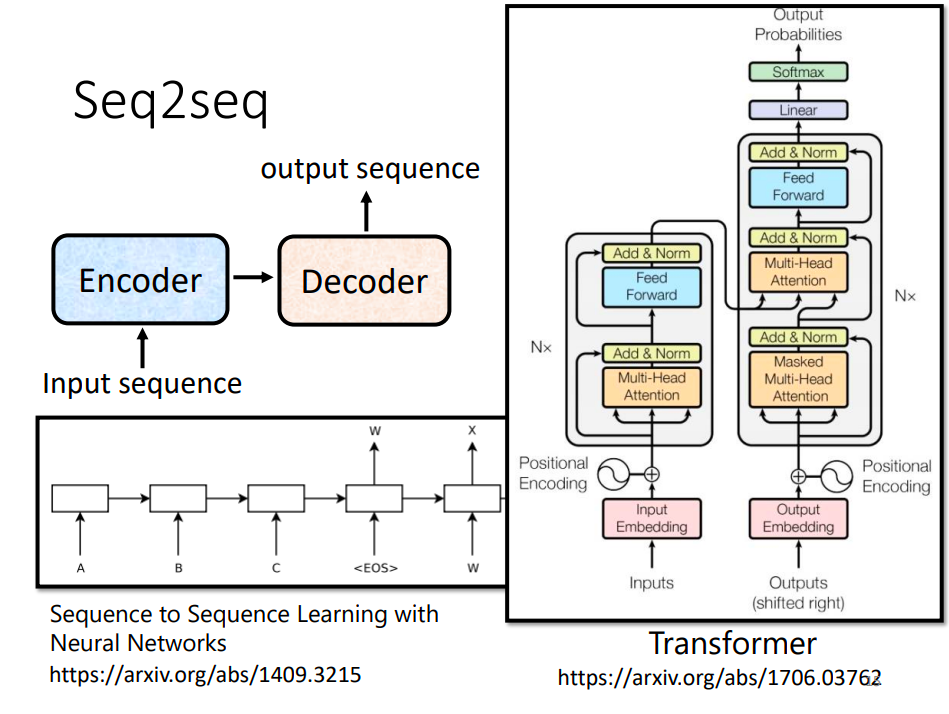
中间这部分是一段多头注意力子层,将Encoder的内容汇合进来结合之前的再传到全连接层,最终经过线性层和Softmax进行输出概率。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号