面试题11：旋转数组的最小数字

目录

• 1 题目
• 2 思路
• 3 代码示例

1 题目

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。

2 思路

我们注意到旋转之后的数组实际上可以划分为两个排序的子数组，而且前面的子数组的元素都大于或者等于后面子数组的元素。我们还注意到最小的元素刚好是这两个子数组的分界线。在排序的数组中我们可以用二分查找法实现O(logn)的查找。本题给出的数组，在一定程度上是排序的，可以用二分查找的思路寻找最小值。以前面的数组{3,4,5,1,2}为例，下图展示了在该数组中查找最小值的过程：

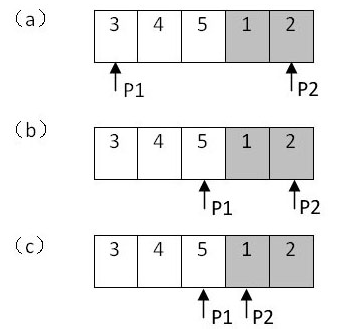
算法步骤：
1.和二分查找法一样，我们用两个指针分别指向数组的第一个元素和最后一个元素。

2.接着我们可以找到数组中间的元素：
　　如果该中间元素位于前面的递增子数组，那么它应该大于或者等于第一个指针指向的元素。此时数组中最小的元素应该位于该中间元素的后面。我们可以把第一个指针指向该中间元素，这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组之中。如果中间元素位于后面的递增子数组，那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小的元素应该位于该中间元素的前面。

3.接下来我们再用更新之后的两个指针，重复做新一轮的查找。

按照上述的思路，第一个指针总是指向前面递增数组的元素，而第二个指针总是指向后面递增数组的元素。最终第一个指针将指向前面子数组的最后一个元素，而第二个指针会指向后面子数组的第一个元素。也就是它们最终会指向两个相邻的元素，而第二个指针指向的刚好是最小的元素。这就是循环结束的条件
除此之外，本题还有两个特殊情况：

1.将数组前0个元素移动到后面（相当于没有旋转，数组整体有序）。明显我们上面的分析没有包含这种情况，需要特殊处理，方法也很简单，将第一个元素和最后一个元素相比，若第一个元素小于最后一个元素，则说明最小值就是的第一个元素，可以直接返回。

2.首尾指针指向的数字和中间元素三者都相等时，无法判断中间元素位于哪个子数组，无法缩小问题规模。此时，只能退而求其次，进行顺序查找。

3 代码示例

/*
三种情况：
（1）把前面0个元素搬到末尾，也就是排序数组本身，第一个就是最小值
（2）一般情况二分查找，当high-low=1时，high就是最小值
（3）如果首尾元素和中间元素都相等时，只能顺序查找
*/
int Min(int* numbers ,int length)
{
	//检查是否有效
	if(numbers==nullptr||length<=0)
		throw std::exception("invalid paramters");
	//指向起始和末尾
	int index1 = 0;
	int index2 = length-1;
	//一旦发现数组中第一个数字小于最后一个数字，表明该数组是排序的就可以直接返回第一个数字了
	int indexMid = index1;
	while(numbers[index1] >= numbers[index2])
	{
		// 如果index1和index2指向相邻的两个数，
		// 则index1指向第一个递增子数组的最后一个数字，
		// index2指向第二个子数组的第一个数字，也就是数组中的最小数字
		if(index2 - index1 ==1)
		{
			indexMid = index2;
			break;
		}
		//中间值
		indexMid = (index1 + index2)/2;
		// 特殊情况：如果下标为index1、index2和indexMid指向的三个数字相等，则只能顺序查找
		if(numbers[index1]==numbers[index2] && numbers[indexMid] == numbers[index1])
			return MinInOrder(numbers,index1,index2);
		// 缩小查找范围
		if(numbers[indexMid]>=numbers[index1])
			index1 = indexMid;
		else if(numbers[indexMid]<=numbers[index2])
			index2 = indexMid;
	}
	return numbers[indexMid];
}
int MinInOrder(int* numbers ,int index1,int index2)
{
	int result = numbers[index1];
	for (int i = index1+1 ;i <= index2;i++)
	{
		if(result >numbers[i])
			result = numbers[i];
	}
	return result;
}