面试题10：斐波那契数列

目录

• 1 题目
• 2 思路
• 3 实用解法
• 4 拓展

1 题目

题目：求斐波那契数列。写一个函数，输入n，求斐波那契数列的第n项。斐波那契数列的定义如下：

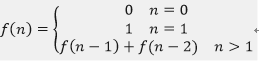
2 思路

效率低的解法：

long long Fibonacci(unsigned int n)
{
	if(n<=0)
		return 0;
	if(n==1)
		return 1;
	return Fibonacci(n-1) + Fibonacci(n-2);
}

如下代码流程图，可以看出这里面有着众多的重复计算。而且重复节点的数会随着n的增大而急剧增加。

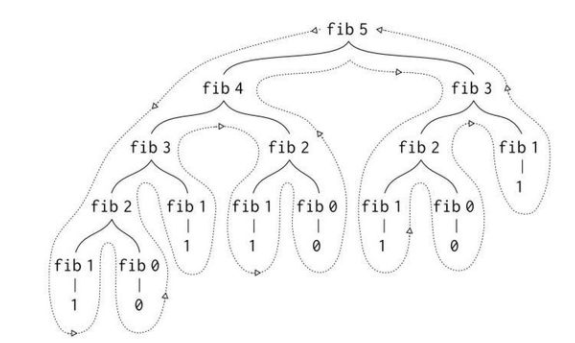
3 实用解法

上述代码之所以慢，是因为重复的计算太多，只需减少重复计算就行。首先根据f（0）和f（1）算出f（2），再根据f（1）和f（2）算出f（3）。。。依次推算就可以第n项。这种思路的时间复杂度是o（n）。实现代码如下：

long long fibonacci(unsigned n)
{
	int result[2]={0,1};
	if(n<2)
		return result[n];
	long long fibMMinusOne =1;
	long long fibMMinusTwo =0;
	long long fibN =0;
	for(unsigned int i=2 ;i<=n ;i++)
	{
		fibN = fibMMinusOne + fibMMinusTwo;
		fibMMinusOne = fibMMinusTwo;
		fibMMinusTwo = fibN;
	}
	return fibN;
}

4 拓展

题目2：青蛙跳台阶问题。
一只青蛙一次可以跳上1级台阶，也可以跳2级台阶。求该青蛙跳上一个n级的台阶总共有多少中跳法。我们把n阶台阶时的跳法看成n的函数，计为f（n），则当n>2 时，有两种一种是从f（n-1）跳一个台阶，一种是从f（n-2）跳2个台阶。即为f（n）=f（n-1）+f（n-2）