面试题7：重建二叉树

目录

• 1 题目
• 2 思路
• 3 代码示例

1 题目

题目：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示的二叉树并输出它的头结点。

2 思路

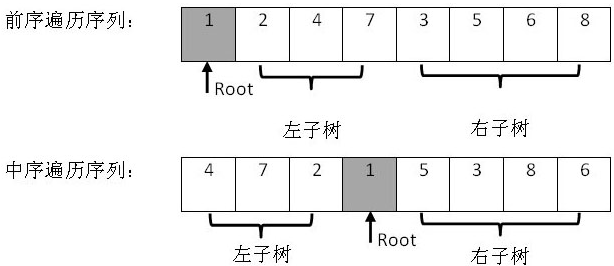
1）首先确定根节点的值。从前序遍历中的得知。
2）根据中序遍历的特点，找到根节点的值，并从中确定左子树的个数，右子树的个数。
3）根据根节点的位置，及左右子树的个数，确定前序遍历及中序遍历中，左右子树。
4）递归处理左右子树

3 代码示例

struct Node
{
    int m_nValue;
    Node *m_pLeft;
    Node *m_pRight;
};

Node *ConstructCore(int *preOrder, int startPreOrder, int endPreOrder, int *inOrder, int startInOrder, int endInOrder)
{
    // 前序遍历序列的第一个数字是根结点的值
    int rootValue = preOrder[startPreOrder];
    Node *root = new Node();
    root->m_nValue = rootValue;
    root->m_pLeft = root->m_pRight = nullptr;

    if (startPreOrder == endPreOrder)
    {
        if (startInOrder == endInOrder && preOrder[startPreOrder] == inOrder[startInOrder])
        {
            return root;
        }
        else
        {
            logic_error ex("XXXXX");
            throw exception(ex);
        }
    }

    // 在中序遍历中找到根结点的值
    int rootInOrder = startInOrder;
    while (rootInOrder <= endInOrder && inOrder[rootInOrder] != rootValue)
    {
        rootInOrder++;
    }
    // 输入的两个序列不匹配的情况
    if (rootInOrder == endInOrder && inOrder[rootInOrder] != rootValue)
    {
        std::logic_error ex("XXXXX");
        throw std::exception(ex);
    }
    int leftLength = rootInOrder - startInOrder;
    int leftPreOrderEnd = startPreOrder + leftLength;
    if (leftLength > 0)
    {
        // 构建左子树
        root->m_pLeft = ConstructCore(preOrder, startPreOrder + 1, leftPreOrderEnd, inOrder, startInOrder, rootInOrder - 1);
    }
    if (leftLength < endPreOrder - startPreOrder)
    {
        // 构建右子树
        root->m_pRight = ConstructCore(preOrder, leftPreOrderEnd + 1, endPreOrder, inOrder, rootInOrder + 1, endInOrder);
    }
    return root;
}

Node *Construct(int *preOrder, int *inOrder, int length)
{
    // 空指针判断
    if (preOrder == nullptr || inOrder == nullptr || length <= 0)
    {
        return nullptr;
    }
    return ConstructCore(preOrder, 0, length - 1, inOrder, 0, length - 1);
}
void LevelOrderBinaryTree(Node *root) //层序遍历二叉树
{
    assert(root);
    queue<Node *> q;

    q.push(root);
    while (!q.empty())
    {
        if (q.front()->m_pLeft != NULL)
            q.push(q.front()->m_pLeft);
        if (q.front()->m_pRight != NULL)
            q.push(q.front()->m_pRight);

        cout << q.front()->m_nValue << " ";
        q.pop();
    }
    cout << endl;
}
int main()
{
    int a[] = {1, 2, 4, 7, 3, 5, 6, 8};
    int b[] = {4, 7, 2, 1, 5, 3, 8, 6};
    Node *bree = Construct(a, b, 8);
    LevelOrderBinaryTree(bree);

    return 0;
}