题解 CF1279F New Year and Handle Change

wqs 二分模板题。

我们可以将大小写分开做，分别求小写时的 min 和大写时的 min。

首先可以发现我们肯定是操作越多次越好，所以我们可以假设正好操作 $k$ 次。设 $f(x)$ 为操作 $x$ 次时的最优答案，我们可以发现 $(x, f(x))$ 构成的函数图像是个下凸壳：

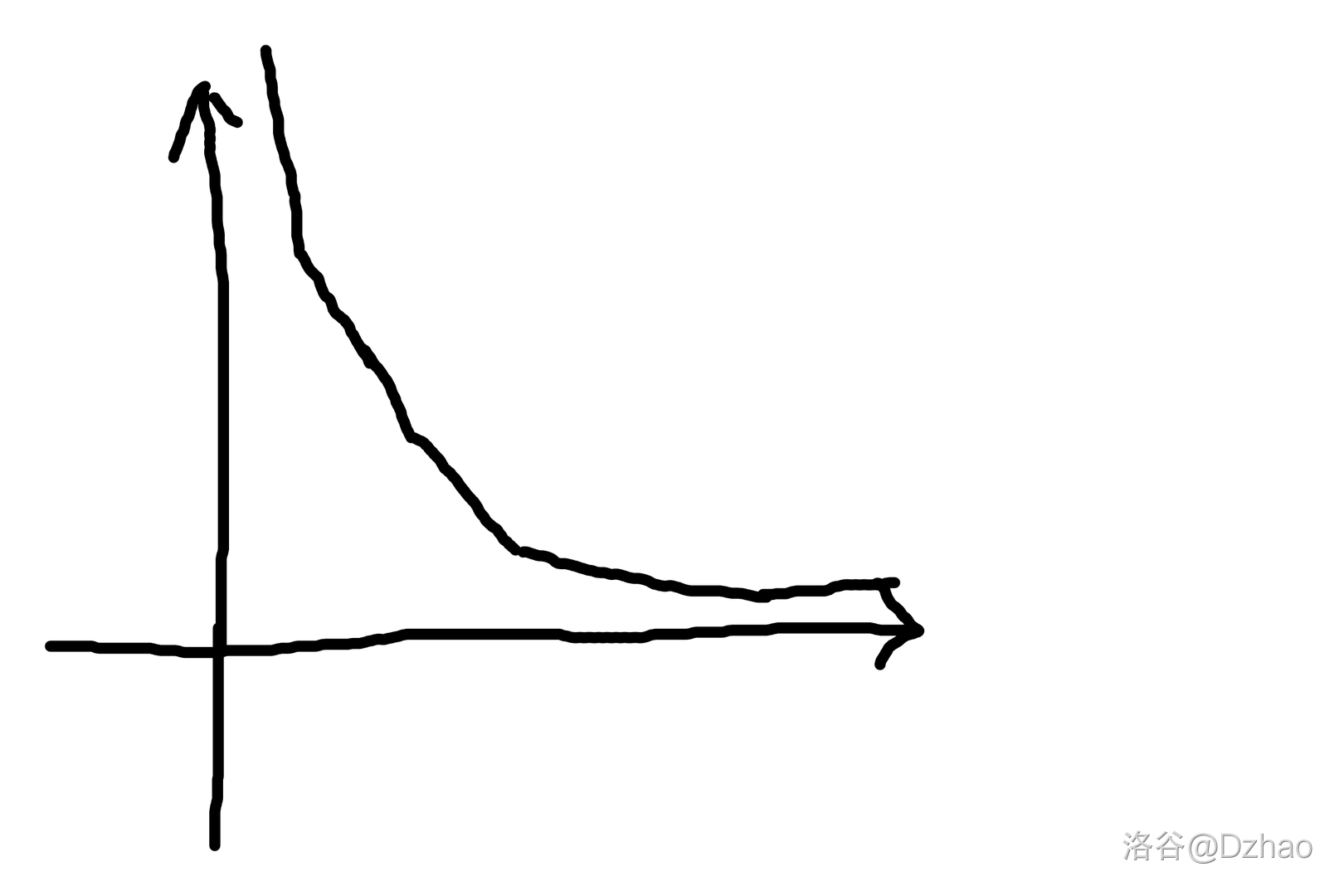
证明：首先 $f(x)$ 肯定是单减的，然后因为你每次操作肯定选最优的操作所以 $f(x)$ 减小的趋势肯定是越来越小的。

然后就是 wqs 二分，我们二分与 $(k, f(k))$ 相切的直线的斜率 $mid$，然后问题就转化为求出这条直线的截距，相当于每次操作每次操作多一个 $-mid$ 的价值，直接 dp 即可，$dp_i$ 表示 $1...i$ 的最优答案。转移是简单的，需注意转移时还需要记录一个当前 $dp_i$ 操作了多少次。

我们求出了截距直接根据斜率即可推出 $f(k)$。

#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
using ll = long long;
const int N = 1e6 + 5;
int n, m, len, a[N], ans = 1e9;
char s[N];
pair <int, int> dp[N];
int check(int mid) {
    for (int i = 1; i <= n; i++) {
        pair <int, int> tmp = dp[i - 1];
        tmp.fi += a[i], dp[i] = tmp;
        tmp = dp[max(i - len, 0)];
        tmp.fi -= mid, tmp.se++;
        dp[i] = min(dp[i], tmp);
    }
    return dp[n].se;
}
void solve() {
    int l = -n, r = 0, p;
    while (l <= r) {
        int mid = l + r >> 1;
        if (check(mid) <= m) l = mid + 1, p = mid;
        else r = mid - 1; 
    }
    check(p);
    ans = min(ans, dp[n].fi + p * m);
}

int main() {
    scanf("%d%d%d%s", &n, &m, &len, s + 1);
    for (int i = 1; i <= n; i++) a[i] = s[i] >= 'a' && s[i] <= 'z'; solve();
    for (int i = 1; i <= n; i++) a[i] ^= 1; solve();
    printf("%d\n", ans);
    return 0;
}