第三章预习

3.1高级语言和机器指令中的运算

• C程序中涉及的运算
  1 按位运算
  C语言中按位运算有：符号|表示按位OR运算；符号&表示按位AND运算；符号~表示按位NOT运算；符号^表示按位XOR运算。
  2 逻辑运算
  C语言中的逻辑运算有：符号||表示OR运算；符号&&表示AND运算；符号！表示NOT运算。
  逻辑运算是非数值计算，其操作数只有两个逻辑值：True和False，通常用非0数表示逻辑值True，用全0数表示逻辑值False。
  3 移位运算
• 移位操作有逻辑移位和算术移位两种。
• 逻辑移位不考虑符号位，总是把高（低）位移出，低（高）位补0。对于无符号整数的逻辑左移，如果最高位移出的是1，则发生溢出。
• 算术移位方式，左移时，高位移出，低位不0，每移一位，如果左移前、后符号为不同，则发生溢出；右移时，低位移出，高位补符号位。
• 每左移一位，相当于数值扩大了一倍，所以左移可能会发生溢出，左移k位，相当于数值乘以2^{k;每右移一位，相当于数值缩小一半，右移k位，相当与数值除以2}k。
  4 位扩展和位截断运算
• 进行位扩展时，扩展后的数值应保持不变。
• 有两种位扩展方式：0扩展和符号扩展。
• 0扩展用于无符号数，只要在短的无符号数前面添加足够的0即可。符号扩展用于补码表示的带符号整数，通过在短的带符号整数前添加足够多的符号位来扩展。
• 位截断发生在将长数转换成短数时。

3.2基本运算部件

• 串行进位加法器
  串行进位（又称行波进位）加法器，逻辑电路比较简单，但是最高位的加法运算，一定要等到所有低位的加法完成之后才进行，低位的进位要逐步的传递到高位，逐级产生进位，因此运算速度较慢。

• 并行进位加法器
  为了提高运算速度，减少延迟时间，可以采用并行进位法，也叫超前进位或先行进位。
  并行进位加法器的运算速度很快，形成最高进位输出的延迟时间很短，但是以增加硬件逻辑线路为代价。
  对于长字长的加法器，往往将加法器分成若干组，在组内采用并行进位，组间采用串行进位或并行进位。

• 带标志加法器
  要能够进行无符号整数的加减运算和带符号整数的加减运算，还需要在无符号数加法器的基础上增加相应的逻辑门电路，使加法器不仅能计算和差还能生成相应的标志性息。

• 算术逻辑部件
  ALU电路：利用集成电路技术可将若干位全加器，并行进位链、输出选择电路等部分集成在一块芯片上，称为多功能算术、逻辑运算部件ALU。

3.3定点运算

• 原码加减运算
  1.比较两个操作数的符号，对加法实行“同号求和，异号求差”，对减法实行“异号求和，同号求差”。
  2.求和时，数值位相加，若最高位产生进位则结果溢出。和的符号位取被加数（被减数）的符号。
  3.求差时，被加数（被减数）数值位加上加数（减数）数值位的补码。

• 补码加减运算
  [x+y]补=[x]补+[y]补(mod 2^n)
  [x-y]补=[x]补+[y]补(mod 2^n)

• 移码加减运算
  

• 原码的乘法运算
  原码一位乘法
  确定乘积的符号位，由两个乘数的符号异或得到。
  计算乘积的数值位，乘积的数值部分为两个乘数的数值部分之积。
  原码二位乘法
  对乘数的每两位取值情况进行判断，使每步求出对应于该两位的部分积，则可将乘法速度提高一倍

• 补码乘法运算
  补码一位乘法
  布斯乘法：将符号位和数值位合在一起参与运算，直接得出用补码表示的乘积，且正数和负数同等对待
  补码乘法运算规则：
  (1)乘数最低位增加一位辅助位Y(-1)=0
  (2)根据Y(i) Y(i-1)的值，决定是“+[x]补”、“-[x]补”还是“+0”
  (3)每次加减后，算术右移一位，得到部分积
  (4)重复(2)(3)步n次，结果得[xy]补
  布斯乘法的运算过程为n次“判断-加减-右移”循环，遇到连续的1或连续的0时，可跳过加法运算直接进行右移操作
  补码两位乘法
  [P(i+2)]补 = 2^(-2) ([P(i)]补 + (Y(i-1) + Y(i) - 2Y(i+1)) [x]补)

• 原码除法运算
  当被除数和除数都不为0，并且商也不可能溢出时，才能进一步进行除法运算
  原码除法运算与原码乘法运算一样，要将符号位和数值位分开来处理，商的符号为相除两数符号的“异或”值，商的数值为两数绝对值之商
  单精度除法，其商的位数一定不会超过n位，因此不会发生溢出；双精度除法，商的位数可能多于n位，因此，可能发生溢出
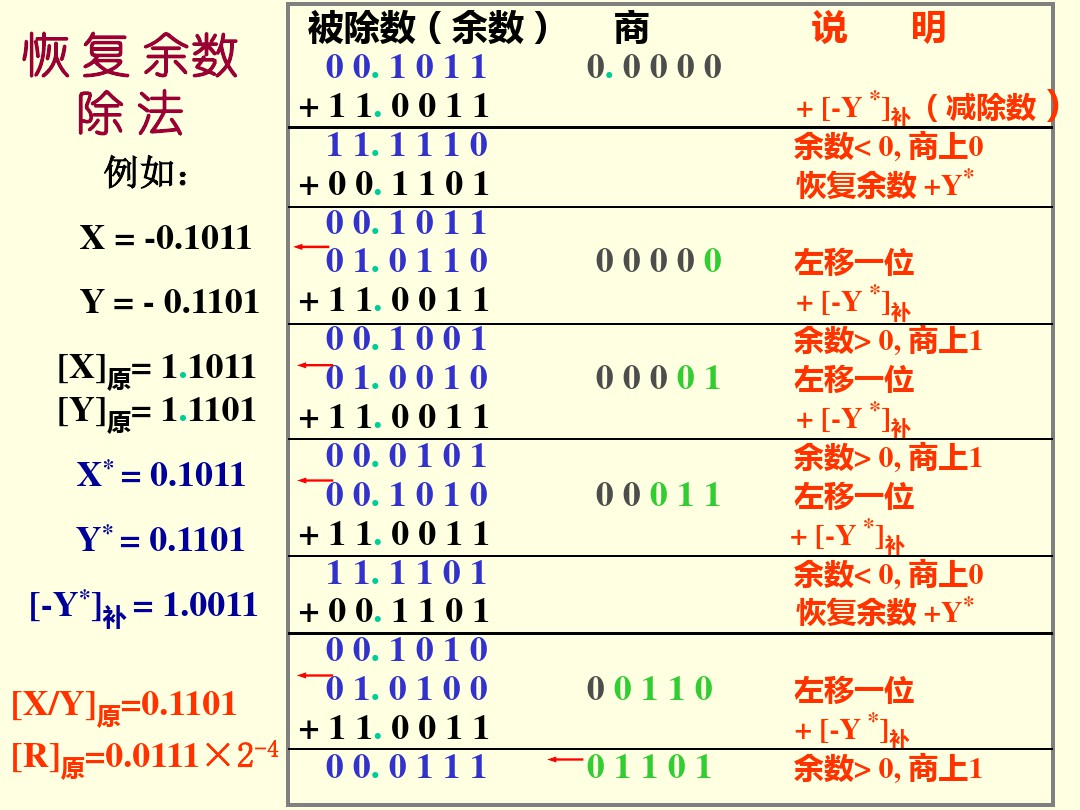
  计算机中两个无符号数除法的运算步骤：
  (1)操作数预置
  (2)做减法试商
  (3)上商为0时恢复余数
  (4)中间余数左移，以便继续试商
  

不恢复余数除法
与恢复余数法的区别：若余数（被除数）为负，表示不够减，商上0，恢复余数（加上除数） ，左移一位，加上[-y]_补 , 加上[ y ] 补 [y]_补[y] 补
​###3.3.8 补码除法运算
首先要对被除数和除数取值、大小等进行相应的判断，以确定除数是否为0，商是否为0，是否溢出。
根据被除数（中间余数）与除数之间符号的异同或差值的正负来确定下次做减法还是加法。

3.4 浮点数运算

• 浮点数加减运算
  1.对阶：使两数的小数点位置对齐。
  2.尾数加减：将对阶后的两尾数按定点加减运算规则求和（差）。
  3.规格化，为增加有效数字的位数，提高运算精度，必须将求和或差后的尾数规格化。
  4.舍入，为提高精度，要考虑尾数有意时丢失的数值位。
  5.判断结果是否溢出。

• 浮点数乘除运算
  两浮点数相乘其乘积的阶码为相乘两数阶码之和,其尾数应为相乘两数的尾数之积。
  两个浮点数相除，商的阶码为被除数的阶码减去除数的阶码得到的差，尾数为被除数的尾数除以除数的尾数所得的商。
  参加运算的两个数都为规格化浮点数，乘除运算都可能出现结果不满足规格化要求的问题，因此也必须进行规格化，舍入和溢出判断等操作。规格化时要修改阶码。

• 运算部件的组成
  ALU、移位器、存放临时数据的寄存器，用于数据选择的多路选择器、实现数据传送的总线构成一个运算数据通路